Druckglieder - Bemessung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Symmetrisch bewehrte Bauteile durch einachsige Biegung und Längskraft beansprucht == Für die Bemessung von Druckgliedern werden bevorzugt Interaktionsdia…“) |
|||
| (13 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | + | <br /> | |
| − | |||
| − | + | ==Klassifizierung== | |
| − | + | Druckglieder sind stabförmige Bauteile mit [[Überwiegend längskraftbeanspruchter Querschnitt|überwiegend längskraftbeanspruchtem Querschnitt]]. | |
| − | und | + | == Symmetrisch bewehrte Bauteile durch einachsige Biegung und Längskraft beansprucht == |
| − | <math>\Sigma | + | Für die Bemessung von Druckgliedern werden bevorzugt Interaktionsdiagramme als Bemessungshilfsmittel herangezogen. Diese Interaktionsdiagramme gelten für symmetrisch bewehrte Querschnitte unter Biegung und Längskraft, wobei die Bewehrung aus der Beziehung zwischen Moment und Normalkraft ermittelt wird. |
| + | Druckglieder werden bei meist wechselseitig wirkenden Momenten üblicherweise symmetrisch bewehrt. Das Interaktionsdiagramm beruht auf den Identitätsbeziehungen: die einwirkenden Schnittgrößen entsprechen den Widerständen. Beim überdrückten Querschnitt (nur Druckspannungen und eine außerhalb des Querschnitts liegende Dehnungs-Nulllinie) eines horizontal gelagerten Balkens ergäbe dies<br /><br /> | ||
| + | :{| | ||
| + | |<math>\Sigma H=0:{{N}_{Ed}}=-\left| {{F}_{cd}} \right|-\left| {{F}_{s1d}} \right|-\left| {{F}_{s2d}} \right|</math> | ||
| + | |}<br /> | ||
| + | (der einwirkenden Normalkraft wirkt die Betondruckkraft und die Stahldruckkraft der beiden Bewehrungslagen oben und unten entgegen)<br /> | ||
| + | und | ||
| + | :{| | ||
| + | |<math>\Sigma M=0:{{M}_{Ed}}=\left| {{F}_{cd}} \right|\cdot \frac{h}{2-a}-\left| {{F}_{s1d}} \right|\cdot \frac{h}{2-{{d}_{1}}}+\left| {{F}_{s2d}} \right|\cdot \frac{h}{2-{{d}_{2}}}</math> | ||
| + | |}<br /> | ||
(dem einwirkenden Moment wirken die Betondruckkraft und die Stahlkräfte jeweils multipliziert mit ihren Hebelarmen entgegen).<br /><br /> | (dem einwirkenden Moment wirken die Betondruckkraft und die Stahlkräfte jeweils multipliziert mit ihren Hebelarmen entgegen).<br /><br /> | ||
| Zeile 17: | Zeile 24: | ||
<br /> | <br /> | ||
| − | Mit <math>{{F}_{cd}}={{\alpha }_{v}}\cdot h\cdot b\cdot {{f}_{cd}}</math> | + | Mit<br /> |
| − | + | :{| | |
| − | + | |<math>{{F}_{cd}}={{\alpha }_{v}}\cdot h\cdot b\cdot {{f}_{cd}}</math> | |
| − | + | |- | |
| − | <math>{{F}_{s1d}}={{A}_{s1}}\cdot \left| {{\sigma }_{s1d}} \right|</math> | + | |<math>{{\alpha }_{v}}=1-\frac{16}{189}\cdot (\left| {{\varepsilon }_{c2}} \right|-2){}^\text{2}</math> |
| − | + | |- | |
| − | + | |<math>{{F}_{s1d}}={{A}_{s1}}\cdot \left| {{\sigma }_{s1d}} \right|</math> | |
| + | |- | ||
| + | |<math>{{F}_{s2d}}={{A}_{s2}}\cdot \left| {{\sigma }_{s2d}} \right|</math> | ||
| + | |}<br /> | ||
ergibt sich | ergibt sich | ||
| + | :{| | ||
| + | |<math>{{N}_{Ed}}=-{{\alpha }_{v}}\cdot h\cdot b\cdot {{f}_{cd}}-{{A}_{s1}}\cdot \left| {{\sigma }_{s1d}} \right|-{{A}_{s2\cdot }}\left| {{\sigma }_{s2d}} \right|</math> | ||
| + | |}<br /><br /> | ||
| − | |||
| − | |||
Bezogen auf die Betonfestigkeit und die Abmessungen erhält man | Bezogen auf die Betonfestigkeit und die Abmessungen erhält man | ||
| + | :{| | ||
| + | |<math>{{\nu }_{Ed}}=-{{\alpha }_{v}}-{{\rho }_{1\cdot }}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{cd}}}-{{\rho }_{2}}\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{cd}}}</math> | ||
| + | |}<br /><br /> | ||
| − | + | mit der bezogenen Normalkraft<br/> | |
| − | + | :{| | |
| − | + | |<math>{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}</math> | |
| − | + | |}<br /> | |
| − | <math>{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}</math> und den Längsbewehrungsgraden < | + | und den Längsbewehrungsgraden<br /> |
| + | :{| | ||
| + | |<math>{{\rho }_{i}}=\frac{{{A}_{si}}}{b\cdot h}</math> | ||
| + | |}<br /><br /> | ||
Der mechanische Bewehrungsgrad als Verhältnis von der Bewehrung aufnehmbaren Normalkraft zu der von dem Beton aufnehmbaren Normalkraft beschreibt sich zu | Der mechanische Bewehrungsgrad als Verhältnis von der Bewehrung aufnehmbaren Normalkraft zu der von dem Beton aufnehmbaren Normalkraft beschreibt sich zu | ||
| − | + | :{| | |
| − | <math>{{\omega }_{i}}={{\rho }_{i}}\cdot \frac{{{f}_{yd}}}{{{f}_{cd}}}</math> | + | |<math>{{\omega }_{i}}={{\rho }_{i}}\cdot \frac{{{f}_{yd}}}{{{f}_{cd}}}</math> |
| − | + | |}<br /> | |
Eingesetzt in die Gleichung für die bezogene Normalkraft ergibt sich | Eingesetzt in die Gleichung für die bezogene Normalkraft ergibt sich | ||
| − | + | :{| | |
| − | <math>{{\nu }_{Ed}}=-{{\alpha }_{v}}-{{\omega }_{1\cdot }}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}-{{\omega }_{2}}\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}</math> | + | |<math>{{\nu }_{Ed}}=-{{\alpha }_{v}}-{{\omega }_{1\cdot }}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}-{{\omega }_{2}}\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}</math> |
| − | + | |}<br /> | |
So gilt außerdem mit dem auf Abmessung und Betonfestigkeit bezogenen Moment <math>{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}</math> und der Gleichung oben aus <math>\Sigma M=0</math> | So gilt außerdem mit dem auf Abmessung und Betonfestigkeit bezogenen Moment <math>{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}</math> und der Gleichung oben aus <math>\Sigma M=0</math> | ||
| − | + | :{| | |
| − | <math>{{\mu }_{Ed}}={{\alpha }_{v}}\cdot \left( \frac{1}{2}-{{k}_{a}} \right)-{{\omega }_{1}}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{1}}}{h} \right)+\omega 2\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{2}}}{h} \right)</math> | + | |<math>{{\mu }_{Ed}}={{\alpha }_{v}}\cdot \left( \frac{1}{2}-{{k}_{a}} \right)-{{\omega }_{1}}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{1}}}{h} \right)+\omega 2\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{2}}}{h} \right)</math> |
| − | + | |} | |
mit<br /> | mit<br /> | ||
| − | + | :{| | |
| − | <math>{{k}_{a}}=\frac{6}{7}\cdot \frac{441-64\cdot {{\left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}^{2}}}{756-64\cdot \left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}</math> | + | |<math>{{k}_{a}}=\frac{6}{7}\cdot \frac{441-64\cdot {{\left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}^{2}}}{756-64\cdot \left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}</math> |
| − | + | |}<br /> | |
| − | <math>{{\varepsilon }_{c2}}~</math> - der Betonstauchung am oberen Bauteilrand.<br /><br /> | + | :{| |
| + | |<math>{{\varepsilon }_{c2}}~</math> - der Betonstauchung am oberen Bauteilrand. | ||
| + | |}<br /><br /> | ||
Vereinfachend sind für die Bemessung mit dem Interaktionsdiagramm die Eingangsgrößen <math>{{\mu }_{Ed}}~</math> und <math>{{\nu }_{Ed}}~</math> notwendig. Außerdem gilt es, die richtige Tafel in Abhängigkeit von <math>\frac{{{d}_{i}}}{h}</math> zu wählen oder gegebenenfalls zu interpolieren. Der damit ermittelte mechanische Bewehrungsgrad ist gleichmäßig auf die Bewehrungslagen zu verteilen.<br /> | Vereinfachend sind für die Bemessung mit dem Interaktionsdiagramm die Eingangsgrößen <math>{{\mu }_{Ed}}~</math> und <math>{{\nu }_{Ed}}~</math> notwendig. Außerdem gilt es, die richtige Tafel in Abhängigkeit von <math>\frac{{{d}_{i}}}{h}</math> zu wählen oder gegebenenfalls zu interpolieren. Der damit ermittelte mechanische Bewehrungsgrad ist gleichmäßig auf die Bewehrungslagen zu verteilen.<br /> | ||
Es ist darauf zu achten, dass die Normalkraft situationsabhängig sowohl günstig als auch ungünstig einwirken kann. Die zugehörigen Bemessungskombinationen sind demnach beide zu verwenden, um für beide Fälle die Bewehrungsmenge zu ermitteln und dann selbstverständlich die größere anzuordnen.<br /> | Es ist darauf zu achten, dass die Normalkraft situationsabhängig sowohl günstig als auch ungünstig einwirken kann. Die zugehörigen Bemessungskombinationen sind demnach beide zu verwenden, um für beide Fälle die Bewehrungsmenge zu ermitteln und dann selbstverständlich die größere anzuordnen.<br /> | ||
| − | Bei gedrungenen Stützen besteht bei mittiger Druckbelastung keine Knickgefahr und es genügt ein vereinfachter Nachweis ohne Berücksichtigung der Einwirkungen nach Theorie II. Ordnung. <br /> | + | Bei [[Schlankheit|gedrungenen]] Stützen besteht bei mittiger Druckbelastung keine Knickgefahr und es genügt ein vereinfachter Nachweis ohne Berücksichtigung der Einwirkungen nach [[Theorie II. Ordnung|Theorie II. Ordnung]]. <br /> |
| − | Die Bemessung schlanker Stützen erfordert eine weiterführende Betrachtung in Hinblick auf den Schnittgrößenzuwachs.<br /> | + | Die Bemessung [[Schlankheit|schlanker]] Stützen erfordert eine weiterführende Betrachtung in Hinblick auf den Schnittgrößenzuwachs.<br /> |
| − | Mittig gedrückte Stützen ohne Momentenbeanspruchung sind stets mit einer Mindestausmitte von <math>{{e}_{0}}=\max \{h/30;20mm\}</math> anzusetzen. Demnach ist von einer Momentenbeanspruchung auszugehen. Bei schlanken Stützen, die ohnehin nach Theorie II. Ordnung zu bemessen sind, gilt diese Bestimmung nicht. | + | Mittig gedrückte Stützen ohne Momentenbeanspruchung sind stets mit einer Mindestausmitte von <math>{{e}_{0}}=\max \{h/30;20mm\}~</math> anzusetzen. Demnach ist von einer Momentenbeanspruchung auszugehen. Bei schlanken Stützen, die ohnehin nach Theorie II. Ordnung zu bemessen sind, gilt diese Bestimmung nicht. |
== Unbewehrte Druckglieder == | == Unbewehrte Druckglieder == | ||
| − | Als unbewehrt gelten Stützen, wenn sie einen Bewehrungsgrad kleiner der Mindestbewehrung aufweisen. Es gilt eine maximal zulässige Betongüte von C35/45.<br /> | + | Als unbewehrt gelten Stützen, wenn sie einen Bewehrungsgrad kleiner der [[Mindestbewehrung|Mindestbewehrung]] aufweisen. Es gilt eine maximal zulässige Betongüte von C35/45.<br /> |
Ab einer Schlankheit von <math>\lambda \ge 8,5</math> sind unbewehrte Druckbauteile stets als schlank anzusehen (bei zweiseitig gehaltenen Druckglieder auch <math>{{l}_{col}}/h<2,5</math>), eine Bemessung nach Theorie II. Ordnung ist also üblicherweise erforderlich. | Ab einer Schlankheit von <math>\lambda \ge 8,5</math> sind unbewehrte Druckbauteile stets als schlank anzusehen (bei zweiseitig gehaltenen Druckglieder auch <math>{{l}_{col}}/h<2,5</math>), eine Bemessung nach Theorie II. Ordnung ist also üblicherweise erforderlich. | ||
Es gelten folgende Bedingungen für die Ausführung unbewehrter Stützen oder Wände:<br /><br /> | Es gelten folgende Bedingungen für die Ausführung unbewehrter Stützen oder Wände:<br /><br /> | ||
| − | |||
| − | |||
| − | + | - <math>\lambda \le 85</math><br /><br /> | |
| + | und<br /><br /> | ||
| − | <math>{{l}_{0}}=\beta \cdot {{l}_{w}}</math> | + | - <math>{{l}_{w}}/{{h}_{w}}\le 25</math> für Pendelstützen und zweiseitig gehaltene Wände.<br /><br /> |
| − | <br /> | + | Die [[Knicklänge/Ersatzstablänge|Knicklänge]] des Druckglieds berechnet sich wie gehabt: |
| + | |||
| + | :{| | ||
| + | |<math>{{l}_{0}}=\beta \cdot {{l}_{w}}</math> | ||
| + | |}<br /> | ||
mit<br /> | mit<br /> | ||
| − | <math>{{l}_{w}}</math> - der Länge des Druckglieds | + | :{| |
| − | β – dem Knickbeiwert.<br /><br /> | + | |<math>{{l}_{w}}</math> - der Länge des Druckglieds |
| + | |- | ||
| + | |β – dem Knickbeiwert. | ||
| + | |}<br /><br /> | ||
Als Duktilitätskriterium gilt eine Höchstausmitte von <math>{{e}_{d}}<0,4h</math>, ermittelt aus der maßgebenden Einwirkungskombination und den berücksichtigten Zusatzausmitten der Imperfektion und der Theorie II. Ordnung. Dadurch wird nie ein Versagen ohne Vorankündigen eintreten.<br /><br /> | Als Duktilitätskriterium gilt eine Höchstausmitte von <math>{{e}_{d}}<0,4h</math>, ermittelt aus der maßgebenden Einwirkungskombination und den berücksichtigten Zusatzausmitten der Imperfektion und der Theorie II. Ordnung. Dadurch wird nie ein Versagen ohne Vorankündigen eintreten.<br /><br /> | ||
| − | Der Nachweis wird geführt mit | + | Der Nachweis wird geführt mit<br /> |
| − | + | :{| | |
| − | <math>{{N}_{Rd,\lambda }}=b\cdot h\cdot {{f}_{cd,pl}}\cdot \Phi </math> | + | |<math>{{N}_{Rd,\lambda }}=b\cdot h\cdot {{f}_{cd,pl}}\cdot \Phi </math> |
| − | + | |}<br /> | |
mit<br /> | mit<br /> | ||
| − | <math>\Phi =1,14\cdot (1-\frac{2{{e}_{tot}}}{h})-0,02\cdot \frac{{{l}_{0}}}{h}</math> | + | :{| |
| − | <math>0\le \Phi \le 1-\frac{2{{e}_{tot}}}{h}</math> | + | |<math>\Phi</math> || = ||<math>1,14\cdot (1-\frac{2{{e}_{tot}}}{h})-0,02\cdot \frac{{{l}_{0}}}{h}</math> |
| − | <math>{{e}_{tot}}={{e}_{0}}+{{e}_{i}}~</math> | + | |- |
| − | <math>{{f}_{cd,pl}}={{\alpha }_{cc,pl}}\cdot {{f}_{ck}}/{{\gamma }_{c}}</math> | + | |<math>0\le \Phi \le 1-\frac{2{{e}_{tot}}}{h}</math> |
| − | <math>{{\alpha }_{cc,pl}}=0,7~</math> | + | |- |
| − | <math>{{\gamma }_{c}}=1,5~</math> | + | |<math>{{e}_{tot}}</math> || = || <math>{{e}_{0}}+{{e}_{i}}~</math> |
| − | <math>{{e}_{0}}</math> - der Ausmitte nach Theorie I. Ordnung | + | |- |
| − | <math>{{e}_{i}}</math> - der ungewollten Ausmitte, es darf angenommen werden: <math>{{e}_{i}}=\frac{{{l}_{0}}}{400}</math> | + | |<math>{{f}_{cd,pl}}</math> || = || <math>{{\alpha }_{cc,pl}}\cdot {{f}_{ck}}/{{\gamma }_{c}}</math> |
| + | |- | ||
| + | |<math>{{\alpha }_{cc,pl}}</math> || = || <math>0,7~</math> | ||
| + | |- | ||
| + | |<math>{{\gamma }_{c}}</math> || = || <math>1,5~</math> | ||
| + | |- | ||
| + | |<math>{{e}_{0}}</math> || - || der Ausmitte nach Theorie I. Ordnung | ||
| + | |- | ||
| + | |<math>{{e}_{i}}</math> || - || der ungewollten Ausmitte, es darf angenommen werden: <math>{{e}_{i}}=\frac{{{l}_{0}}}{400}</math> | ||
| + | |} | ||
Der Faktor <math>\varphi </math> berücksichtigt hierbei auf vereinfachende Art und Weise die Auswirkungen nach Theorie II. Ordnung. | Der Faktor <math>\varphi </math> berücksichtigt hierbei auf vereinfachende Art und Weise die Auswirkungen nach Theorie II. Ordnung. | ||
| Zeile 103: | Zeile 137: | ||
== Symmetrisch bewehrte Bauteile durch zweiachsige Biegung und Längskraft beansprucht == | == Symmetrisch bewehrte Bauteile durch zweiachsige Biegung und Längskraft beansprucht == | ||
| + | |||
| + | Die Bemessung erfolgt bei zu vernachlässigender Einwirkung nach Theorie II. Ordnung mit einem ähnlichen Interaktionsdiagramm wie für einachsige Biegung. Die bezogenen Schnittgrößen sind wie bekannt<br /> | ||
| + | |||
| + | |||
| + | <math>\begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}\\{{\mu }_{1}}=\max \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}\\{{\mu }_{2}}=\min \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}\\{{\mu }_{Ed,y}}=\frac{\left| {{M}_{Ed,y}} \right|}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}\\{{\mu }_{Ed,z}}=\frac{\left| {{M}_{Ed,z}} \right|}{b{}^\text{2}\cdot h\cdot {{f}_{cd}}}\end{array}</math> | ||
| + | |||
| + | Weitere Eingangsgrößen sind das Verhältnis von <math>\frac{{{d}_{1}}}{h}</math> und <math>\frac{{{b}_{1}}}{b}</math>, wobei <math>{{b}_{1}}~</math> das Pendant zu <math>{{h}_{1}}~</math> in die andere Querschnittsrichtung darstellt. Nach Ermittlung des mechanischen Bewehrungsgrades gilt es diesen gleichmäßig auf die für das Interaktionsdiagramm erstellte Bewehrungsanordnung zu verteilen. | ||
| + | |||
| + | <br /> | ||
| + | ==Quellen== | ||
| + | |||
| + | <references /> | ||
| + | <br /> | ||
| + | |||
| + | {{Seiteninfo | ||
| + | |Quality-flag = [[File:quality-flag-white.gif|right|70px]] | ||
| + | |Status = Seite in Bearbeitung, es gibt Hinweise zur Verbesserung | ||
| + | }} | ||
| + | |||
| + | |||
| + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
Aktuelle Version vom 27. Oktober 2019, 19:25 Uhr
Klassifizierung
Druckglieder sind stabförmige Bauteile mit überwiegend längskraftbeanspruchtem Querschnitt.
Symmetrisch bewehrte Bauteile durch einachsige Biegung und Längskraft beansprucht
Für die Bemessung von Druckgliedern werden bevorzugt Interaktionsdiagramme als Bemessungshilfsmittel herangezogen. Diese Interaktionsdiagramme gelten für symmetrisch bewehrte Querschnitte unter Biegung und Längskraft, wobei die Bewehrung aus der Beziehung zwischen Moment und Normalkraft ermittelt wird.
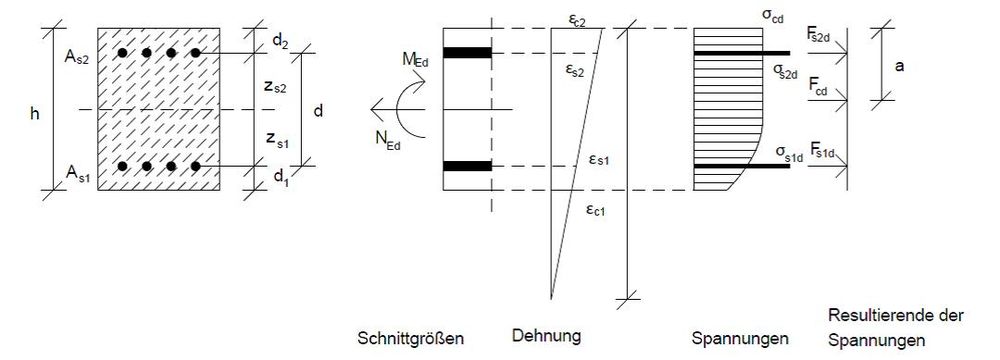
Druckglieder werden bei meist wechselseitig wirkenden Momenten üblicherweise symmetrisch bewehrt. Das Interaktionsdiagramm beruht auf den Identitätsbeziehungen: die einwirkenden Schnittgrößen entsprechen den Widerständen. Beim überdrückten Querschnitt (nur Druckspannungen und eine außerhalb des Querschnitts liegende Dehnungs-Nulllinie) eines horizontal gelagerten Balkens ergäbe dies
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma H=0:{{N}_{Ed}}=-\left| {{F}_{cd}} \right|-\left| {{F}_{s1d}} \right|-\left| {{F}_{s2d}} \right|}
(der einwirkenden Normalkraft wirkt die Betondruckkraft und die Stahldruckkraft der beiden Bewehrungslagen oben und unten entgegen)
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma M=0:{{M}_{Ed}}=\left| {{F}_{cd}} \right|\cdot \frac{h}{2-a}-\left| {{F}_{s1d}} \right|\cdot \frac{h}{2-{{d}_{1}}}+\left| {{F}_{s2d}} \right|\cdot \frac{h}{2-{{d}_{2}}}}
(dem einwirkenden Moment wirken die Betondruckkraft und die Stahlkräfte jeweils multipliziert mit ihren Hebelarmen entgegen).
Mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{F}_{cd}}={{\alpha }_{v}}\cdot h\cdot b\cdot {{f}_{cd}}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{v}}=1-\frac{16}{189}\cdot (\left| {{\varepsilon }_{c2}} \right|-2){}^\text{2}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{F}_{s1d}}={{A}_{s1}}\cdot \left| {{\sigma }_{s1d}} \right|} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{F}_{s2d}}={{A}_{s2}}\cdot \left| {{\sigma }_{s2d}} \right|}
ergibt sich
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed}}=-{{\alpha }_{v}}\cdot h\cdot b\cdot {{f}_{cd}}-{{A}_{s1}}\cdot \left| {{\sigma }_{s1d}} \right|-{{A}_{s2\cdot }}\left| {{\sigma }_{s2d}} \right|}
Bezogen auf die Betonfestigkeit und die Abmessungen erhält man
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu }_{Ed}}=-{{\alpha }_{v}}-{{\rho }_{1\cdot }}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{cd}}}-{{\rho }_{2}}\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{cd}}}}
mit der bezogenen Normalkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}}
und den Längsbewehrungsgraden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\rho }_{i}}=\frac{{{A}_{si}}}{b\cdot h}}
Der mechanische Bewehrungsgrad als Verhältnis von der Bewehrung aufnehmbaren Normalkraft zu der von dem Beton aufnehmbaren Normalkraft beschreibt sich zu
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{i}}={{\rho }_{i}}\cdot \frac{{{f}_{yd}}}{{{f}_{cd}}}}
Eingesetzt in die Gleichung für die bezogene Normalkraft ergibt sich
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu }_{Ed}}=-{{\alpha }_{v}}-{{\omega }_{1\cdot }}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}-{{\omega }_{2}}\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}}
So gilt außerdem mit dem auf Abmessung und Betonfestigkeit bezogenen Moment Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}} und der Gleichung oben aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Sigma M=0}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{Ed}}={{\alpha }_{v}}\cdot \left( \frac{1}{2}-{{k}_{a}} \right)-{{\omega }_{1}}\cdot \frac{\left| {{\sigma }_{s1d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{1}}}{h} \right)+\omega 2\cdot \frac{\left| {{\sigma }_{s2d}} \right|}{{{f}_{yd}}}\cdot \left( \frac{1}{2}-\frac{{{d}_{2}}}{h} \right)}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{k}_{a}}=\frac{6}{7}\cdot \frac{441-64\cdot {{\left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}^{2}}}{756-64\cdot \left( \left| {{\varepsilon }_{c2}} \right|-2 \right)}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{c2}}~} - der Betonstauchung am oberen Bauteilrand.
Vereinfachend sind für die Bemessung mit dem Interaktionsdiagramm die Eingangsgrößen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{Ed}}~}
und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu }_{Ed}}~}
notwendig. Außerdem gilt es, die richtige Tafel in Abhängigkeit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{d}_{i}}}{h}}
zu wählen oder gegebenenfalls zu interpolieren. Der damit ermittelte mechanische Bewehrungsgrad ist gleichmäßig auf die Bewehrungslagen zu verteilen.
Es ist darauf zu achten, dass die Normalkraft situationsabhängig sowohl günstig als auch ungünstig einwirken kann. Die zugehörigen Bemessungskombinationen sind demnach beide zu verwenden, um für beide Fälle die Bewehrungsmenge zu ermitteln und dann selbstverständlich die größere anzuordnen.
Bei gedrungenen Stützen besteht bei mittiger Druckbelastung keine Knickgefahr und es genügt ein vereinfachter Nachweis ohne Berücksichtigung der Einwirkungen nach Theorie II. Ordnung.
Die Bemessung schlanker Stützen erfordert eine weiterführende Betrachtung in Hinblick auf den Schnittgrößenzuwachs.
Mittig gedrückte Stützen ohne Momentenbeanspruchung sind stets mit einer Mindestausmitte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}=\max \{h/30;20mm\}~}
anzusetzen. Demnach ist von einer Momentenbeanspruchung auszugehen. Bei schlanken Stützen, die ohnehin nach Theorie II. Ordnung zu bemessen sind, gilt diese Bestimmung nicht.
Unbewehrte Druckglieder
Als unbewehrt gelten Stützen, wenn sie einen Bewehrungsgrad kleiner der Mindestbewehrung aufweisen. Es gilt eine maximal zulässige Betongüte von C35/45.
Ab einer Schlankheit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda \ge 8,5}
sind unbewehrte Druckbauteile stets als schlank anzusehen (bei zweiseitig gehaltenen Druckglieder auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{col}}/h<2,5}
), eine Bemessung nach Theorie II. Ordnung ist also üblicherweise erforderlich.
Es gelten folgende Bedingungen für die Ausführung unbewehrter Stützen oder Wände:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda \le 85}
und
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{w}}/{{h}_{w}}\le 25}
für Pendelstützen und zweiseitig gehaltene Wände.
Die Knicklänge des Druckglieds berechnet sich wie gehabt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}=\beta \cdot {{l}_{w}}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{w}}} - der Länge des Druckglieds β – dem Knickbeiwert.
Als Duktilitätskriterium gilt eine Höchstausmitte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{d}}<0,4h}
, ermittelt aus der maßgebenden Einwirkungskombination und den berücksichtigten Zusatzausmitten der Imperfektion und der Theorie II. Ordnung. Dadurch wird nie ein Versagen ohne Vorankündigen eintreten.
Der Nachweis wird geführt mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Rd,\lambda }}=b\cdot h\cdot {{f}_{cd,pl}}\cdot \Phi }
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Phi} = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,14\cdot (1-\frac{2{{e}_{tot}}}{h})-0,02\cdot \frac{{{l}_{0}}}{h}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0\le \Phi \le 1-\frac{2{{e}_{tot}}}{h}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}} = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}+{{e}_{i}}~} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{cd,pl}}} = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc,pl}}\cdot {{f}_{ck}}/{{\gamma }_{c}}} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc,pl}}} = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,7~} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{c}}} = Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1,5~} Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}} - der Ausmitte nach Theorie I. Ordnung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}} - der ungewollten Ausmitte, es darf angenommen werden: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}=\frac{{{l}_{0}}}{400}}
Der Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi } berücksichtigt hierbei auf vereinfachende Art und Weise die Auswirkungen nach Theorie II. Ordnung.
Symmetrisch bewehrte Bauteile durch zweiachsige Biegung und Längskraft beansprucht
Die Bemessung erfolgt bei zu vernachlässigender Einwirkung nach Theorie II. Ordnung mit einem ähnlichen Interaktionsdiagramm wie für einachsige Biegung. Die bezogenen Schnittgrößen sind wie bekannt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}\\{{\mu }_{1}}=\max \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}\\{{\mu }_{2}}=\min \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}\\{{\mu }_{Ed,y}}=\frac{\left| {{M}_{Ed,y}} \right|}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}\\{{\mu }_{Ed,z}}=\frac{\left| {{M}_{Ed,z}} \right|}{b{}^\text{2}\cdot h\cdot {{f}_{cd}}}\end{array}}
Weitere Eingangsgrößen sind das Verhältnis von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{d}_{1}}}{h}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{b}_{1}}}{b}} , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{b}_{1}}~} das Pendant zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{h}_{1}}~} in die andere Querschnittsrichtung darstellt. Nach Ermittlung des mechanischen Bewehrungsgrades gilt es diesen gleichmäßig auf die für das Interaktionsdiagramm erstellte Bewehrungsanordnung zu verteilen.
Quellen
Seiteninfo
|