Mindestbewehrung deckengleicher Unterzug (Bsp.): Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Tlange (Diskussion | Beiträge) K (→Berechnung) |
|||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | |||
| + | <br /> | ||
| + | |||
== Aufgabe == | == Aufgabe == | ||
Ermittlung der Mindestbewehrung eines deckengleichen Unterzuges am Zwischenauflager anhand folgender Ausgangssituation:<br /> | Ermittlung der Mindestbewehrung eines deckengleichen Unterzuges am Zwischenauflager anhand folgender Ausgangssituation:<br /> | ||
| Zeile 44: | Zeile 47: | ||
:<math>A_\mathrm{s,min} = \cfrac{1820kN}{15,03cm*50kN/cm^2} = \underline{\underline{2,42cm^2}}</math><br /><br /> | :<math>A_\mathrm{s,min} = \cfrac{1820kN}{15,03cm*50kN/cm^2} = \underline{\underline{2,42cm^2}}</math><br /><br /> | ||
:<math>A_\mathrm{gew} = \underline{\underline{3,14cm^2}}</math><br /><br /> | :<math>A_\mathrm{gew} = \underline{\underline{3,14cm^2}}</math><br /><br /> | ||
| + | |||
| + | ===== Ausdruck in mb-AEC Baustatik ===== | ||
[[File:Mindestbewehrung (Bsp.) 1.JPG|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | [[File:Mindestbewehrung (Bsp.) 1.JPG|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | ||
==== Querkraftbewehrung ==== | ==== Querkraftbewehrung ==== | ||
| − | * Rechnerisch erforderlich?<br /> | + | * Rechnerisch erforderlich?<br /><br /> |
:<math>V_\mathrm{Ed} \le V_\mathrm{Rd,c}</math><br /><br /> | :<math>V_\mathrm{Ed} \le V_\mathrm{Rd,c}</math><br /><br /> | ||
| Zeile 56: | Zeile 61: | ||
:::<math>\rho_\mathrm{l} = \cfrac{A_\mathrm{sl}}{b_\mathrm{w}*d} = \cfrac{3,14cm^2}{44,00cm*15,70cm} = \underline{0,00455} < 0,02</math><br /><br /> | :::<math>\rho_\mathrm{l} = \cfrac{A_\mathrm{sl}}{b_\mathrm{w}*d} = \cfrac{3,14cm^2}{44,00cm*15,70cm} = \underline{0,00455} < 0,02</math><br /><br /> | ||
::<math>V_\mathrm{Rd,c} = [\cfrac{0,15}{1,5}*2,00*(100*0,00455*25n/mm^2)^{1/3}+0] * 440mm*157mm = 31061N= \underline{31,06kN}</math><br /><br /> | ::<math>V_\mathrm{Rd,c} = [\cfrac{0,15}{1,5}*2,00*(100*0,00455*25n/mm^2)^{1/3}+0] * 440mm*157mm = 31061N= \underline{31,06kN}</math><br /><br /> | ||
| − | ::<math>V_\mathrm{Rd,c} | + | ::<math>V_\mathrm{Rd,c} \ge [v_\mathrm{min}+0,12*\sigma_\mathrm{cp}] * b_\mathrm{w}*d~</math><br /><br /> |
:::<math>v_\mathrm{min} = \cfrac{0,0525}{\gamma_\mathrm{c}}*k^{3/2} *f_\mathrm{ck}^{1/2} = \cfrac{0,0525}{1,5}*2,00^{3/2} *(25kN/cm^2)^{1/2} = \underline{0,495} < 0,02</math><br /><br /> | :::<math>v_\mathrm{min} = \cfrac{0,0525}{\gamma_\mathrm{c}}*k^{3/2} *f_\mathrm{ck}^{1/2} = \cfrac{0,0525}{1,5}*2,00^{3/2} *(25kN/cm^2)^{1/2} = \underline{0,495} < 0,02</math><br /><br /> | ||
| − | ::<math>V_\mathrm{Rd,c} | + | ::<math>V_\mathrm{Rd,c} \ge [0,495+0] * 440mm*157mm = 34193N = \underline{34,19kN}~</math><br /><br /> |
:<math>V_\mathrm{Ed} \le V_\mathrm{Rd,c}</math><br /><br /> | :<math>V_\mathrm{Ed} \le V_\mathrm{Rd,c}</math><br /><br /> | ||
| − | :<math>29,72kN \le 34,19kN</math><br /><br /> | + | :<math>\underline{\underline{29,72kN \le 34,19kN}}</math><br /><br /> |
| + | |||
| + | *Mindestquerkraftbewehrung ist nicht erforderlich!<br /><br /> | ||
| − | + | ===== Ausdruck in mb-AEC Baustatik ===== | |
[[File:Mindestbewehrung (Bsp.) 2.JPG|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | [[File:Mindestbewehrung (Bsp.) 2.JPG|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | ||
| Zeile 69: | Zeile 76: | ||
<references /> | <references /> | ||
| − | == | + | {{Seiteninfo(mb) |
| − | + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | |
| − | + | |Status = Seite fertig, ungeprüft| | |
| − | + | |Modul-Version = 2014.011 | |
| − | + | }} | |
| − | [[Kategorie:Beispiele]] | + | [[Kategorie:Beispiele-Stahlbetonbau]] |
Aktuelle Version vom 11. November 2019, 17:13 Uhr
Aufgabe
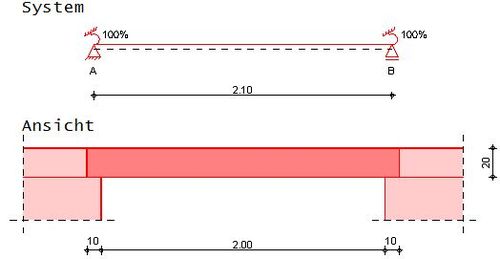
Ermittlung der Mindestbewehrung eines deckengleichen Unterzuges am Zwischenauflager anhand folgender Ausgangssituation:
Maße
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Deckendicke~h = 0,20m}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Wanddicke~t = 0,24m}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Lichte~Stuetzweite~l_\mathrm{n} = 2,00m}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Plattenstuetzweite~l_\mathrm{P,o} = 6,00m}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Plattenstuetzweite~l_\mathrm{P,u} = 4,00m}
Statische Nutzhöhe
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_\mathrm{o} = 15,70cm~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_\mathrm{1,o} = 4,30cm~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_\mathrm{u} = 16,70cm~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_\mathrm{1,u} = 3,30cm~}
Mitwirkende Plattenbreiten (Zwischenauflager)
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{M,F} = 105,00cm~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{M,S} = 52,50cm~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{M,Q} = 44,00cm~}
Baustoffe
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Beton~C25/30~(XC1)~mit~f_\mathrm{ck} =25 N/mm^2}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Betonstahl~Bst~500~S~(A)~mit~f_\mathrm{yk} =500 N/mm^2}
Einwirkungen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} = 29,72kN~}
Sicherheitsbeiwerte
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}\gamma_\mathrm{C} =1,50\end{align}}
Berechnung
Längsbewehrung
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_\mathrm{s,min} = \cfrac{M_\mathrm{cr}}{z_\mathrm{II}*f_\mathrm{yk}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{cr} = f_\mathrm{ctm} * \cfrac{I_\mathrm{I}}{z_\mathrm{I}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{ctm} = \underline{0,26kN/cm^2}~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{I} = \cfrac{b*h^3}{12} = \cfrac{105cm*(20cm)^3}{12} = \underline{70000cm^4}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z_\mathrm{I} = \cfrac{h}{2} = \cfrac{20cm}{2} = \underline{10cm}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{ctm} = \underline{0,26kN/cm^2}~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{cr} = 0,26kN/cm^2 * \cfrac{70000cm^4}{10cm} = \underline{1820kN}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z_\mathrm{II} = 0,9*d = 0,9*16,70cm = \underline{15,03cm}~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{cr} = f_\mathrm{ctm} * \cfrac{I_\mathrm{I}}{z_\mathrm{I}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_\mathrm{s,min} = \cfrac{1820kN}{15,03cm*50kN/cm^2} = \underline{\underline{2,42cm^2}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_\mathrm{gew} = \underline{\underline{3,14cm^2}}}
Ausdruck in mb-AEC Baustatik
Querkraftbewehrung
- Rechnerisch erforderlich?
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} \le V_\mathrm{Rd,c}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,c} = [\cfrac{0,15}{\gamma_\mathrm{c}}*k*(100*\rho_\mathrm{l}*f_\mathrm{ck})^{1/3}+0,12*\sigma_\mathrm{cp}] * b_\mathrm{w}*d}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = 1+\sqrt{\cfrac{200}{d}} = 1+\sqrt{\cfrac{200}{157mm}} = \underline{2,13} >2,0}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_\mathrm{l} = \cfrac{A_\mathrm{sl}}{b_\mathrm{w}*d} = \cfrac{3,14cm^2}{44,00cm*15,70cm} = \underline{0,00455} < 0,02}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = 1+\sqrt{\cfrac{200}{d}} = 1+\sqrt{\cfrac{200}{157mm}} = \underline{2,13} >2,0}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,c} = [\cfrac{0,15}{1,5}*2,00*(100*0,00455*25n/mm^2)^{1/3}+0] * 440mm*157mm = 31061N= \underline{31,06kN}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,c} \ge [v_\mathrm{min}+0,12*\sigma_\mathrm{cp}] * b_\mathrm{w}*d~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_\mathrm{min} = \cfrac{0,0525}{\gamma_\mathrm{c}}*k^{3/2} *f_\mathrm{ck}^{1/2} = \cfrac{0,0525}{1,5}*2,00^{3/2} *(25kN/cm^2)^{1/2} = \underline{0,495} < 0,02}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_\mathrm{min} = \cfrac{0,0525}{\gamma_\mathrm{c}}*k^{3/2} *f_\mathrm{ck}^{1/2} = \cfrac{0,0525}{1,5}*2,00^{3/2} *(25kN/cm^2)^{1/2} = \underline{0,495} < 0,02}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,c} \ge [0,495+0] * 440mm*157mm = 34193N = \underline{34,19kN}~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd,c} = [\cfrac{0,15}{\gamma_\mathrm{c}}*k*(100*\rho_\mathrm{l}*f_\mathrm{ck})^{1/3}+0,12*\sigma_\mathrm{cp}] * b_\mathrm{w}*d}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} \le V_\mathrm{Rd,c}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{\underline{29,72kN \le 34,19kN}}}
- Mindestquerkraftbewehrung ist nicht erforderlich!
Ausdruck in mb-AEC Baustatik
Quellen
Seiteninfo
|