|
|
| (7 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| − | Diese Seite ist noch in Bearbeitung.
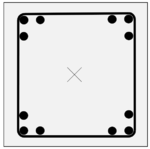
| + | [[Datei:Nennsteifigkeit Einführung.png|right|thumb|150px|Stützenquerschnitt]] |
| | + | Dieses Berechnungsbeispiel verdeutlicht die Vorgehensweise bei der Bemessung einer Stahlbetonstütze nach dem Verfahren mit Nennsteifigkeit. |
| | | | |
| | == Aufgabenstellung == | | == Aufgabenstellung == |
| Zeile 15: |
Zeile 16: |
| | * Nutzlast (Stützenkopf) <math>N_{Qk} = - 750,0 kN</math> (Nutzlastkategorie C) | | * Nutzlast (Stützenkopf) <math>N_{Qk} = - 750,0 kN</math> (Nutzlastkategorie C) |
| | * Bewehrungsvorschlag: Øs,L =20 mm, Øs,Bü =20 mm | | * Bewehrungsvorschlag: Øs,L =20 mm, Øs,Bü =20 mm |
| − |
| |
| | | | |
| | Es ist die vollständige Bemessung nach dem Verfahren mit Nennsteifigkeit durchzuführen und entsprechende Bewehrung auszuwählen! | | Es ist die vollständige Bemessung nach dem Verfahren mit Nennsteifigkeit durchzuführen und entsprechende Bewehrung auszuwählen! |
| Zeile 142: |
Zeile 142: |
| | | | |
| | ===== Beiwert für den Momentenverlauf ===== | | ===== Beiwert für den Momentenverlauf ===== |
| − | | + | [[Datei:Verfahren mit Nennsteifigkeit (Bsp.) 3.png|rechts|mini|100px|Momentenverlauf infolge Imperfektion]] |
| | Das Moment stammt aus der Lastausmitte <math>e_i</math> für Imperfektionen. Hierbei handelt es sich um eine ungewollte Schiefstellung der Stütze, deshalb ist der Momentenverlauf dreieckig, damit gilt <math>c_0 = 12</math>. | | Das Moment stammt aus der Lastausmitte <math>e_i</math> für Imperfektionen. Hierbei handelt es sich um eine ungewollte Schiefstellung der Stütze, deshalb ist der Momentenverlauf dreieckig, damit gilt <math>c_0 = 12</math>. |
| − |
| |
| − | Platzhalter für Bild Schiefstellung
| |
| | | | |
| | <math>\beta = \frac{\pi^2}{c_0} = \frac{\pi^2}{12} = 0,822 | | <math>\beta = \frac{\pi^2}{c_0} = \frac{\pi^2}{12} = 0,822 |
| Zeile 153: |
Zeile 151: |
| | ===== Vorläufiges Moment nach Theorie II. Ordnung ===== | | ===== Vorläufiges Moment nach Theorie II. Ordnung ===== |
| | | | |
| − | <math>M_{Ed} = M{0Ed} \cdot (1 + \frac{\beta}{N_B/N_{Ed} - 1}) = 3.431 kNcm \cdot (1 + \frac{0,822}{1.154,9 kN / 2.812,5 kN - 1}) = 3.431 kNcm = 3.431 kNcm \ cdot (-0,39) | + | <math>M_{Ed} = M{0Ed} \cdot (1 + \frac{\beta}{N_B/N_{Ed} - 1})</math> |
| | + | |
| | + | <math>= 3.431 kNcm \cdot (1 + \frac{0,822}{1.154,9 kN / 2.812,5 kN - 1}) = 3.431 kNcm = 3.431 kNcm \cdot { \color{red}(-0,39)} |
| | </math> | | </math> |
| | | | |
| | Der Beiwert zur Erhöhung des Moments nach Theorie I. Ordnung ist negativ geworden, weil die Knicklast <math>N_B</math> kleiner ist als die einwirkende Normalkraft <math>N_{Ed}</math>. Damit liefert die Formel kein brauchbares Ergebnis. Die Vorbemessung muss deshalb mit alternativem Ansatz durchgeführt werden. | | Der Beiwert zur Erhöhung des Moments nach Theorie I. Ordnung ist negativ geworden, weil die Knicklast <math>N_B</math> kleiner ist als die einwirkende Normalkraft <math>N_{Ed}</math>. Damit liefert die Formel kein brauchbares Ergebnis. Die Vorbemessung muss deshalb mit alternativem Ansatz durchgeführt werden. |
| | + | |
| | + | ==== Alternativer Ansatz zur (groben) Vorbemessung ==== |
| | | | |
| | <math>M_{Ed} = |N_{Ed}| \cdot \frac{h}{20} = |- 2.812,5 kN| \cdot \frac{35 cm}{20} = 4.922 kNcm = 49,22 kNm | | <math>M_{Ed} = |N_{Ed}| \cdot \frac{h}{20} = |- 2.812,5 kN| \cdot \frac{35 cm}{20} = 4.922 kNcm = 49,22 kNm |
| Zeile 182: |
Zeile 184: |
| | </math> | | </math> |
| | | | |
| − | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle) | + | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (z.B. im Schneider<ref>Albert, Andrej (Hg.): Schneider Bautabellen für Ingenieure, Köln 2018 (23. Auflage).</ref>) |
| | | | |
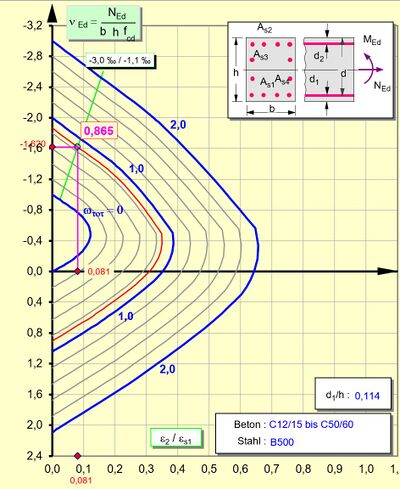
| | + | [[Datei:Verfahren mit Nennsteifigkeit Interaktionsdiagramm 1.JPG|randlos|ohne|400px|Interaktionsdiagramm]] |
| | <math>{\omega}_{tot} = 0,865 | | <math>{\omega}_{tot} = 0,865 |
| | </math> | | </math> |
| Zeile 191: |
Zeile 194: |
| | | | |
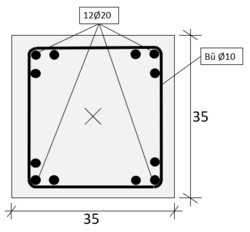
| | Gewählt: <math>12 \O 20 mm</math> mit <math>A_{s,vorh} = 37,68 cm^2</math> | | Gewählt: <math>12 \O 20 mm</math> mit <math>A_{s,vorh} = 37,68 cm^2</math> |
| | + | |
| | + | '''Skizze:''' |
| | + | [[File:Verfahren mit Nennsteifigkeit (Bsp.) 2.png|randlos|ohne|250px|Gewählte Bewehrung]]<br /> |
| | + | Auf Grundlage dieser Vorbemessung kann nun die Nennsteifigkeit des Querschnitts bestimmt werden. |
| | | | |
| | | | |
| Zeile 210: |
Zeile 217: |
| | ==== Flächenträgheitsmoment der Bewehrung ==== | | ==== Flächenträgheitsmoment der Bewehrung ==== |
| | | | |
| − | Platzhalter für Skizze
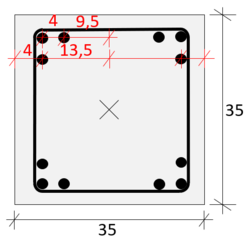
| + | [[File:Verfahren mit Nennsteifigkeit (Bsp.) 4.png|randlos|ohne|250px|Gewählte Bewehrung mit Abstand zum Mittelpunkt Querschnitt]] |
| | | | |
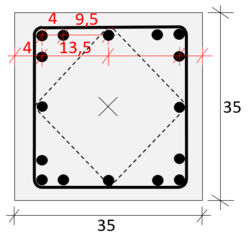
| | Insgesamt <math>12 \O 20 mm</math> mit je <math>A_s = 3,14 cm^2</math>. | | Insgesamt <math>12 \O 20 mm</math> mit je <math>A_s = 3,14 cm^2</math>. |
| | + | |
| | Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. | | Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. |
| | + | |
| | 8 Stäbe mit Abstand <math>s_1 = 13,5 cm</math> und 4 Stäbe mit Abstand <math>s_2 = 9,5 cm</math>. | | 8 Stäbe mit Abstand <math>s_1 = 13,5 cm</math> und 4 Stäbe mit Abstand <math>s_2 = 9,5 cm</math>. |
| | | | |
| − | <math>I_s = 12 \cdot \frac{\pi \cdot d^4}{64} + 8 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2 = 12 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 8 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2 = 9 cm^4 + 4.578 cm^4 + 1.134 cm^4 = 5.721 cm^4 | + | <math>I_s = 12 \cdot \frac{\pi \cdot d^4}{64} + 8 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2</math> |
| | + | |
| | + | <math>= 12 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 8 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2 </math> |
| | + | |
| | + | <math>= 9 cm^4 + 4.578 cm^4 + 1.134 cm^4 = 5.721 cm^4 |
| | </math> | | </math> |
| | | | |
| Zeile 248: |
Zeile 261: |
| | </math> | | </math> |
| | | | |
| − | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle) | + | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung |
| | | | |
| | <math>{\omega}_{tot} = 1,22 | | <math>{\omega}_{tot} = 1,22 |
| Zeile 265: |
Zeile 278: |
| | ==== Flächenträgheitsmoment der Bewehrung ==== | | ==== Flächenträgheitsmoment der Bewehrung ==== |
| | | | |
| − | Platzhalter für Skizze
| + | [[File:Verfahren mit Nennsteifigkeit (Bsp.) 5.png|randlos|ohne|250px|Gewählte Bewehrung mit Abstand zum Mittelpunkt Querschnitt]] |
| | + | |
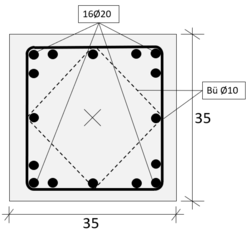
| | + | Insgesamt <math>16 \O 20 mm</math> mit je <math>A_s = 3,14 cm^2</math>. Die vier zusätzlichen Stäbe werden in der Mitte der Seiten angebracht. Zusätzlich werden diagonale Bügel eingeplant. |
| | | | |
| − | Insgesamt <math>16 \O 20 mm</math> mit je <math>A_s = 3,14 cm^2</math>.
| |
| | Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. | | Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. |
| | + | |
| | 10 Stäbe mit Abstand <math>s_1 = 13,5 cm</math>, 4 Stäbe mit Abstand <math>s_2 = 9,5 cm</math> und 2 Stäbe mit Abstand s_3 = 0 cm</math>. | | 10 Stäbe mit Abstand <math>s_1 = 13,5 cm</math>, 4 Stäbe mit Abstand <math>s_2 = 9,5 cm</math> und 2 Stäbe mit Abstand s_3 = 0 cm</math>. |
| | | | |
| − | <math>I_s = 16 \cdot \frac{\pi \cdot d^4}{64} + 10 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2 = 16 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 10 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2 = 13 cm^4 + 5.723 cm^4 + 1.134 cm^4 = 6.870 cm^4 | + | <math>I_s = 16 \cdot \frac{\pi \cdot d^4}{64} + 10 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2</math> |
| | + | |
| | + | <math>= 16 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 10 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2</math> |
| | + | |
| | + | <math> = 13 cm^4 + 5.723 cm^4 + 1.134 cm^4 = 6.870 cm^4 |
| | </math> | | </math> |
| | | | |
| Zeile 303: |
Zeile 322: |
| | </math> | | </math> |
| | | | |
| − | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle) | + | → Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung |
| | | | |
| | <math>{\omega}_{tot} = 1,045 | | <math>{\omega}_{tot} = 1,045 |
| Zeile 314: |
Zeile 333: |
| | </math> | | </math> |
| | | | |
| − | Platzhalter Bewehrungsskizze
| + | [[File:Verfahren mit Nennsteifigkeit (Bsp.) 6.png|randlos|ohne|250px|Finale Bewehrungsskizze]] |
| | + | |
| | + | |
| | + | ==Quellen== |
| | + | |
| | + | <references /> |
| | + | |
| | + | [[Kategorie:Beispiele-Stahlbetonbau]] |
Dieses Berechnungsbeispiel verdeutlicht die Vorgehensweise bei der Bemessung einer Stahlbetonstütze nach dem Verfahren mit Nennsteifigkeit.
Aufgabenstellung
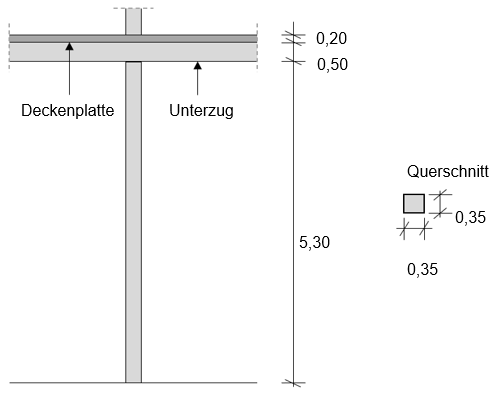
Gegeben ist die dargestellte Hochbau-Innenstütze. Das Gesamt-Bauwerk ist in Richtung der Zeichenebene und senkrecht dazu ausgesteift. Die Stütze wird planmäßig ausschließlich durch Normalkräfte belastet und kann in beide Richtungen ausweichen.
Weiterhin sind folgende Informationen gegeben:
- Beton C25/30 (Innenbauteil – XC 1)
- Stahl B 500 A
- Ständige Last (Stützenkopf)

- Nutzlast (Stützenkopf)
 (Nutzlastkategorie C)
(Nutzlastkategorie C)
- Bewehrungsvorschlag: Øs,L =20 mm, Øs,Bü =20 mm
Es ist die vollständige Bemessung nach dem Verfahren mit Nennsteifigkeit durchzuführen und entsprechende Bewehrung auszuwählen!
Handrechnung
Schnittgrößen nach Theorie I. Ordnung


Knicklänge

 für das gegebene statische System (Pendelstütze)
für das gegebene statische System (Pendelstütze)

Schlankheit und Überprüfung der Notwendigkeit des Nachweises nach Theorie II. Ordnung





Es ist ein Nachweis nach Theorie II. Ordnung nötig.
Nennsteifigkeit
E-Moduln


Flächenträgheitsmoment des Betons

Planmäßige Lastausmitte und Lastausmitte aus Imperfektionen




Vorbemessung
Wirksame Bauteildicke

Endkriechzahl
Erstbelastung des Betons:  Tage
Tage
Bauteil in Innenräumen, trockene Umgebungsbedingungen
 nach Schneider 5.33
nach Schneider 5.33
Moment mit Imperfektionen in quasi-ständiger und GZT-Kombination


Effektive Kriechzahl

Steifigkeitsbeiwerte nach einfacher Formel


Vorläufige Nennsteifigkeit

Knicklast

Beiwert für den Momentenverlauf
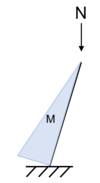
Momentenverlauf infolge Imperfektion
Das Moment stammt aus der Lastausmitte  für Imperfektionen. Hierbei handelt es sich um eine ungewollte Schiefstellung der Stütze, deshalb ist der Momentenverlauf dreieckig, damit gilt
für Imperfektionen. Hierbei handelt es sich um eine ungewollte Schiefstellung der Stütze, deshalb ist der Momentenverlauf dreieckig, damit gilt  .
.

Vorläufiges Moment nach Theorie II. Ordnung


Der Beiwert zur Erhöhung des Moments nach Theorie I. Ordnung ist negativ geworden, weil die Knicklast  kleiner ist als die einwirkende Normalkraft
kleiner ist als die einwirkende Normalkraft  . Damit liefert die Formel kein brauchbares Ergebnis. Die Vorbemessung muss deshalb mit alternativem Ansatz durchgeführt werden.
. Damit liefert die Formel kein brauchbares Ergebnis. Die Vorbemessung muss deshalb mit alternativem Ansatz durchgeführt werden.
Alternativer Ansatz zur (groben) Vorbemessung




Vorbemessung mit Bewehrungswahl



→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (z.B. im Schneider[1])


Gewählt:  mit
mit 
Skizze:
Auf Grundlage dieser Vorbemessung kann nun die Nennsteifigkeit des Querschnitts bestimmt werden.
Genauere Steifigkeitsbeiwerte




Flächenträgheitsmoment der Bewehrung
Insgesamt  mit je
mit je  .
.
Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts.
8 Stäbe mit Abstand  und 4 Stäbe mit Abstand
und 4 Stäbe mit Abstand  .
.



Bemessung
Nennsteifigkeit

Knicklast

Bemessungsmoment nach Theorie II. Ordnung

Bewehrungswahl


→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung


Damit ist  . Der Nachweis ist nicht erfüllt, die Bewehrung muss entweder von der Anzahl oder dem Durchmesser her erhöht werden.
. Der Nachweis ist nicht erfüllt, die Bewehrung muss entweder von der Anzahl oder dem Durchmesser her erhöht werden.
Iteration: Mehr Bewehrungsstäbe
Erhöhung von  auf
auf  . Neues
. Neues  .
.
Flächenträgheitsmoment der Bewehrung
Insgesamt  mit je
mit je  . Die vier zusätzlichen Stäbe werden in der Mitte der Seiten angebracht. Zusätzlich werden diagonale Bügel eingeplant.
. Die vier zusätzlichen Stäbe werden in der Mitte der Seiten angebracht. Zusätzlich werden diagonale Bügel eingeplant.
Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts.
10 Stäbe mit Abstand  , 4 Stäbe mit Abstand
, 4 Stäbe mit Abstand  und 2 Stäbe mit Abstand s_3 = 0 cm</math>.
und 2 Stäbe mit Abstand s_3 = 0 cm</math>.



Bemessung
Nennsteifigkeit

Knicklast

Bemessungsmoment nach Theorie II. Ordnung

Bewehrungswahl


→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung



Quellen
- ↑ Albert, Andrej (Hg.): Schneider Bautabellen für Ingenieure, Köln 2018 (23. Auflage).