Mitwirkende Plattenbreite - Vergleichsrechnung: Unterschied zwischen den Versionen

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen
(Die Seite wurde neu angelegt: „<br /> Geschichtliche Entwicklung der Berechnung der mitwirkenden Plattenbreite und Vergleich zwischen den Berechnungsmethoden des letzten Jahrhunderts, dem Eu…“)
 
 
(3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<br />
+
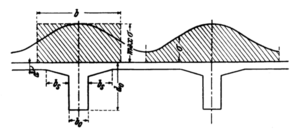
[[Datei:Mitwirkende Plattenbreite - Vergleichsrechnung 0.png|right|thumb|300px|Historische Abbildung zur Berechnung der mitwirkenden Plattenbreite aus <ref> Pucher, A: Lehrbuch des Stahlbetonbaues - Grundlagen und Anwendungen im Hoch- und Brückenbau</ref> ]]
−
Geschichtliche Entwicklung der Berechnung der mitwirkenden Plattenbreite und Vergleich zwischen den Berechnungsmethoden des letzten Jahrhunderts, dem Eurocode, der Berechnung in anderen Ländern und einer FE-Berechnung.
+
Diese Seite zeigt die Zusammenfassung der geschichtlichen Entwicklung der mitwirkenden Plattenbreite sowie den  Vergleich zwischen den Berechnungsmethoden des letzten Jahrhunderts und dem dem Eurocode. Zusätzlich werden Berechnungsvarianten aus Normen außerhalb des Eurocodes und eine FE-Berechnung vorgestellt und verglichen.
−
<br />
 
 
<br />
 
<br />
  
  
 
==Geschichtliche Entwicklung bis zum Eurocode==
 
==Geschichtliche Entwicklung bis zum Eurocode==
−
Die folgende Auflistung dient einem Überblick über die geschichtlichen Entwicklung zur Berechnung der mitwirkenden Plattenbreite. Die Formeln entsprechen keiner aktuell geltenden Norm und werden in der Vergleichsrechnung mit dargestellt. Es handelt sich jeweils um Annäherungsformeln, die einerseits das Problem möglichst genau darstellen sollen, andererseits aber für den täglichen Gebrauch entwickelt wurden. Der Kompromiss, dass die Ergebnisse nicht immer die wirtschaftlichste Lösung darstellen, wurde und wird auch heute im normalen Hochbau hingenommen.
+
Die folgende Auflistung gibt einen kurzen Überblick über die geschichtlichen Entwicklung zur Berechnung der mitwirkenden Plattenbreite. Für eine Übersicht zur Problematik un zu den Berechnungsgrundlagen - siehe [[Mitwirkende Plattenbreite]].
  
−
<!-->
 
−
===Beginn des zwanzigsten Jahrhunderts===
 
−
Das zunächst „''Eisenbetonbau''“ genannte Fachgebiet deutscher Ingenieure begann zu Anfang des zwanzigsten Jahrhunderts den Vorteil von Plattenbalken zu erforschen. 1906 entwickelte zunächst ''Emil Mörsch'' anwendbare Leitsätze mit dem Ziel, wirtschaftliche und vertrauenswürdige Eisenbetonbauten fertigen zu können. Die wirksame Plattenbreite begrenzt er auf ein Drittel der Spannweite. <ref>c
 
−
:<math>b_{eff} = 1/3 \cdot l_{eff}</math> <br />
 
−
Mit der Einführung der ''"Deutschen Industrie Norm"'' (DIN) im Jahr 1918 entstand eine erste Normung für die mitwirkende Plattenbreite, die nach Frank im Jahr 1914 kleiner als ein Drittel beziehungsweise ein Viertel der Spannweite, auf jeden Fall jedoch kleiner als der Abstand zweier Unterzüge sein sollte. <ref>Frank, W.: Eisenbetonbau: Kurzgefasstes Lehrbuch unter besonderer Berücksichtigung der Bedürfnisse der Praxis. 2. vollständig umgearbeitete Auflage. Stuttgart : Verlag von Konrad Wittwer, 1914</ref>
 
−
:<math>b_{eff} = min 1/3 \cdot l_{eff}</math> <br />
 
−
<-->
 
  
 
====1906====
 
====1906====
Zeile 20: Zeile 12:
 
<br />
 
<br />
 
:<math>b_{eff} = \cfrac{1}{3} \cdot l_{eff}</math>  
 
:<math>b_{eff} = \cfrac{1}{3} \cdot l_{eff}</math>  
 +
wobei:
 +
:{|
 +
|-
 +
| b<sub>eff</sub>... || Mitwirkende Plattenbreite
 +
|-
 +
| l<sub>eff</sub>... || Effektive Stützweite
 +
|}<br />
  
 
====1918====
 
====1918====
−
Erste Normung innerhalb der 1918 veröffentlichten "Deutschen Industrie Norm" nach ''Frank.'' <ref>Frank, W.: Eisenbetonbau: Kurzgefasstes Lehrbuch unter besonderer Berücksichtigung der Bedürfnisse der Praxis. 2. vollständig umgearbeitete Auflage. Stuttgart : Verlag von Konrad Wittwer, 1914</ref>  
+
Erste Normung innerhalb der 1918 veröffentlichten "Deutschen Industrie Norm" nach ''Frank.'' In der Norm ist nicht geregelt, für welchen Fall man welche Formel wählt. Es handelt sich um grobe, unbegründete Abschätzungen. <ref>Frank, W.: Eisenbetonbau: Kurzgefasstes Lehrbuch unter besonderer Berücksichtigung der Bedürfnisse der Praxis. 2. vollständig umgearbeitete Auflage. Stuttgart : Verlag von Konrad Wittwer, 1914</ref>  
 
<br />
 
<br />
 
:<math>b_{eff} = min \left( \cfrac{1}{3} \cdot l_{eff} bzw. \cfrac{1}{4} \cdot l_{eff}; b \right) </math>  
 
:<math>b_{eff} = min \left( \cfrac{1}{3} \cdot l_{eff} bzw. \cfrac{1}{4} \cdot l_{eff}; b \right) </math>  
 +
wobei:
 +
:{|
 +
|-
 +
| b<sub>eff</sub>... || Mitwirkende Plattenbreite
 +
|-
 +
| l<sub>eff</sub>... || Effektive Stützweite
 +
|-
 +
| b... || Tatsächlich vorhandene Plattenbreite
 +
|}<br />
  
 
====1943====
 
====1943====
 
''Timoshenko's'' Elastizitätstheorie führt zur "strengen Theorie des Plattenbalkens", die mittels AIRYscher Spannungsfunktion berechnet werden kann. Die Berechnung ist jedoch sehr umständlich, daher gelten fortan die deutschen Bestimmungen nach ''Schleicher'' <ref>Schleicher, Ferdinand: Taschenbuch für Bauingenieure. Berlin, Heidelberg : Springer Berlin Heidelberg, 1955. – ISBN 978–3–642–88349–1</ref>  
 
''Timoshenko's'' Elastizitätstheorie führt zur "strengen Theorie des Plattenbalkens", die mittels AIRYscher Spannungsfunktion berechnet werden kann. Die Berechnung ist jedoch sehr umständlich, daher gelten fortan die deutschen Bestimmungen nach ''Schleicher'' <ref>Schleicher, Ferdinand: Taschenbuch für Bauingenieure. Berlin, Heidelberg : Springer Berlin Heidelberg, 1955. – ISBN 978–3–642–88349–1</ref>  
−
<br />
 
−
:<math>b_{eff} = min \left( b_w + 2 \cdot b_s + 12 \cdot h_f; b_w + 18 \cdot h_f; \cfrac{l_{eff}}{2}; b \right) </math>
 
  
 +
:<math>b_{eff}={min}
 +
\begin{cases}
 +
b_w + 2 \cdot b_s + 12 \cdot h_f \\
 +
b_w + 18 \cdot h_f \\
 +
l_{eff}/2 \\
 +
b
 +
\end{cases}</math><br />
 +
wobei:
 +
:{|
 +
|-
 +
| b<sub>eff</sub>... || Mitwirkende Plattenbreite
 +
|-
 +
| l<sub>eff</sub>... || Effektive Stützweite
 +
|-
 +
| b<sub>w</sub>... || Stegbreite
 +
|-
 +
| b<sub>s</sub>... || Breite der Vouten
 +
|-
 +
| h<sub>f</sub>... || Plattendicke
 +
|-
 +
| b... || Tatsächlich vorhandene Plattenbreite
 +
|}<br />
 
====1960====
 
====1960====
−
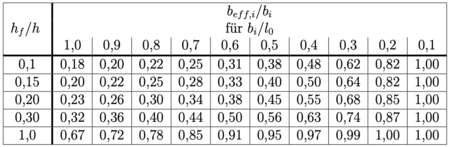
''Brendel'' fasst im Jahr das Wissen um die mitwirkende Plattenbreite kompakt zusammen. Der Fachartikel "Die mitwirkende Plattenbreite nach Theorie und Versuch" ist noch heute von großer Bedeutung. Lässt man FE-Methoden außen vor, sind die Betrachtungen aus 1960 in Kombination mit den sich darauf beziehenden Untersuchungen von ''Leonhardt'' die genausten Näherungen. So lässt sich die bezogenen mitwirkende Plattenbreite (<math>b_{eff}/b_i</math>) über die Verhältnisse <math>h_f/h</math> und <math>b_i/l_0</math> bestimmen.  
+
''Brendel'' fasst im Jahr 1960 das Wissen um die mitwirkende Plattenbreite kompakt zusammen. Der Fachartikel "Die mitwirkende Plattenbreite nach Theorie und Versuch" ist noch heute von großer Bedeutung. Lässt man FE-Methoden außen vor, sind die Betrachtungen aus 1960 in Kombination mit den sich darauf beziehenden Untersuchungen von ''Leonhardt'' die umfassendsten Näherungen. So lässt sich die bezogenen mitwirkende Plattenbreite (<math>b_{eff}/b_i</math>) über die Verhältnisse <math>h_f/h</math> und <math>b_i/l_0</math> bestimmen.  
 
:<math>b_{eff} = b_w + b_1 + b_2 </math>  <br />
 
:<math>b_{eff} = b_w + b_1 + b_2 </math>  <br />
−
Hieraus ergibt sich dann mithilfe der Tabelle der bezogenen mitwirkenden Plattenbreite, die richtige mitwirkende Plattenbreite. Über die Berücksichtigung der Plattendicke wird hier auch die Biegesteifigkeit der Platte einbezogen. Zudem wird die Art des Systems einberechnet. Auch einschnürungserzeugende Einzellasten werden erstmals über einen Abminderungsfaktor η berücksichtigt. <ref>Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In:
+
wobei:
−
Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900</ref> <ref>Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6</ref>
+
:{|
 +
|-
 +
| b<sub>eff</sub>... || Mitwirkende Plattenbreite
 +
|-
 +
| b<sub>w</sub>... || Stegbreite
 +
|-
 +
| b<sub>i</sub>... || Tatsächlich vorhandene einseitige Plattenbreite
 +
|-
 +
| b... || Tatsächlich vorhandene Plattenbreite
 +
|}<br />
 +
[[Datei:Mitwirkende Plattenbreite - Vergleichsrechnung 1.png|right|thumb|450px|Bestimmung der bezogenen mitwirkenden Plattenbreite <ref Name = "Leonhardt"> Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6 </ref> <br />]]
 +
 
 +
Hieraus ergibt sich dann mithilfe der Tabelle der bezogenen mitwirkenden Plattenbreite, die angenäherte mitwirkende Plattenbreite. Über die Berücksichtigung der Plattendicke wird hier auch die Biegesteifigkeit der Platte einbezogen. Zudem wird mittels l<sub>0</sub> die Art des Systems in Form der Momentennulldurchgänge einberechnet. <br />
 +
Auch einschnürungserzeugende Einzellasten werden erstmals über einen Abminderungsfaktor η berücksichtigt. Aus der Tabelle ist abzulesen, dass die Einschnürung vor allem bei kleinen Stützweiten einen Einfluss hat und abgemindert werden muss. <ref>Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In:
 +
Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900</ref> <ref>Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6</ref> Je größer die Stützweite im Verhältnis zur Plattenbreite ist, desto kleiner ist der zu berücksichtigende Einfluss der Einschnürung. Dieses Tragverhalten wird später auch von ''Schleeh'' anhand von Vergleichsberechnungen genauer erklärt und belegt. <ref>Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900</ref>
 +
{|class="wikitable"
 +
|+ Abminderungsfaktor &eta; für konzentrierte Einzellasten
 +
|-
 +
| b<sub>i</sub> / l<sub>0</sub/> || 2,0 || 1,0 || 0,8 || 0,6 || 0,4 || 0,2 || 0,1
 +
|-
 +
| &eta; || 0,6 || 0,61 || 0,62 || 0,63 || 0,65 || 0,7 || 0,9
 +
|}
  
 
==== 1978 ====
 
==== 1978 ====
−
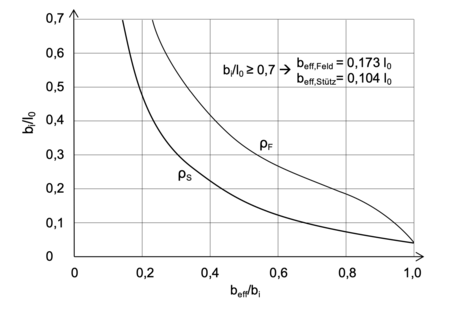
In der DIN 1075 für Betonbrücken aus dem Jahr 1978 ist die Elastizitätstheorie Grundlage der Berechnung. Der Plattenbalken wird demnach getrennt betrachtet, sodass an den Verbindungsstellen zwischen Platte und Balken nur Schubkräfte übertragen werden können. Diese Längsdruckspannungen nehmen dann nach Scheibentheorie mit Abstand zum Balken ab. Die DIN 1075 unterscheidet dabei zwei Fälle:
+
 
 +
[[Datei:Mitwirkende Plattenbreite - Vergleichsrechnung 2.png|right|thumb|450px|Bestimmung der bezogenen mitwirkenden Breite im Stützbereich(S) und Feldbereich(F) nach DIN 1075 (angelehnt an ''Grasser'')]]
 +
 
 +
In der DIN 1075 für Betonbrücken aus dem Jahr 1978 ist die Elastizitätstheorie Grundlage der Berechnung. Der Plattenbalken wird demnach in Platte und Balken unterteilt. Dabei wird die Annahme getroffen, dass an den Verbindungsstellen zwischen Platte und Balkenwerden nur Schubkräfte übertragen werden können. <ref>Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900</ref> Diese Längsdruckspannungen nehmen dann nach Scheibentheorie mit Abstand zum Balken ab. Die DIN 1075 unterscheidet dabei zwei Fälle:
  
 
: 1. <math> \cfrac{b}{l_0} < 0,3 </math> -> Die Platte darf über die gesamte Breite als mittragend angesetzt werden. <br />
 
: 1. <math> \cfrac{b}{l_0} < 0,3 </math> -> Die Platte darf über die gesamte Breite als mittragend angesetzt werden. <br />
−
: 1. <math> \cfrac{b}{l_0} \ge 0,3 </math> -> Ermittlung der mittragenden Plattenbreite mittels folgender Formel: <br />
+
: 2. <math> \cfrac{b}{l_0} \ge 0,3 </math> -> Ermittlung der mittragenden Plattenbreite mittels folgender Formel: <br />
  
−
::<math> b_{eff} = \rho _{F} \cdot b </math>
+
::<math> b_{eff} = \rho _{F} \cdot b </math>wobei:
 +
:{|
 +
|-
 +
| <math>\rho _{F}</math>... || Beiwert für den Feldbereich (siehe Diagramm)
 +
|-
 +
| b... || Tatsächlich vorhandene Plattenbreite
 +
|}<br />
  
−
====1980 - ====
+
====1980 - heute ====
−
Ab 1980 machen vor allem die computergestützten Berechnungsmethoden mittels finiten Elementen große Fortschritte. Auch hier handelt es sich bei der Berechnung um Annäherungen und bis heute gilt der Plattenbalken als eines der schwierigsten Probleme im Stahlbetonbau. Die FE-Berechnungen sind dabei sehr genau, allerdings auch aufwendig und kommt vor allem bei Sonderbauten zum Einsatz.
+
Ab 1980 machen vor allem die computergestützten Berechnungsmethoden mittels finiten Elementen große Fortschritte. Auch hier handelt es sich bei den bisher vorliegenden Berechnungen um Annäherungen, da verschiedene Einflussfaktoren, wie der Einfluss der Bewehrung und Rissbildung, dabei nicht berücksichtigt werden. Die FE-Berechnungen sind dabei sehr genau und kommen vor allem bei Sonderbauten zum Einsatz. <ref>Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45</ref> <ref>Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)</ref>
  
  
 
==Berechnung außerhalb des Eurocodes==
 
==Berechnung außerhalb des Eurocodes==
−
Die Normen zur Berechnung der mitwirkenden Plattenbreite variieren in den verschiedenen Ländern der Welt. Viele orientieren sich dabei am Eurocode, einige am ACI, andere Länder nutzen veraltete Näherungsmethoden. Folgend sollen einige aktuelle Formeln aus Normen aller Welt vorgestellt werden.
+
Die Regeln zur Berechnung der mitwirkenden Plattenbreite variieren in den Normen der verschiedenen Ländern der Welt. Viele orientieren sich dabei am Eurocode, einige am ACI, andere Länder nutzen veraltete Näherungsmethoden. Folgend sollen einige aktuelle Formeln aus Normen aller Welt vorgestellt werden.
  
 
===USA – ACI 318-19 <ref>ACI 318-19: Building Code Requirements for Structural Concrete. American Concrete Institute</ref>===
 
===USA – ACI 318-19 <ref>ACI 318-19: Building Code Requirements for Structural Concrete. American Concrete Institute</ref>===
Zeile 74: Zeile 132:
 
==Vergleichsrechnungen==
 
==Vergleichsrechnungen==
 
===Methodik===
 
===Methodik===
−
Zur besseren Beurteilung der verschiedenen Berechnungsvarianten, wird eine Vergleichsrechnung zwischen den geschichtlichen Methoden und den aktuellen Normen aller Welt durchgeführt. Dabei soll dargestellt werden, ob sich die verschiedenen Annäherungsformeln mit denen aus dem Eurocode und der FE-Berechnung decken und welche Abweichungen es gibt. Es werden jeweils das Innenfeld eines Durchlaufträgers von mehreren Plattenbalken des normalen Hochbaus betrachtet, die mit einer konstanten Streckenlast belastet werden. Übliche Vorgehensweise beim Vergleich der Ergebnisse ist die Nutzung der bezogenen mitwirkenden Plattenbreite <math>\cfrac{b_{eff}}{b}</math> (y-Achse) und dem Verhältnis zwischen der maximalen Plattenbreite zur Stützweite <math>\cfrac{b}{l_{eff}}</math> (x-Achse). Da nicht jede Norm <math>l_0</math> als Anhaltspunkt für die Berechnung enthält, werden die Momentennulldurchgänge in den jeweiligen Berechnungen separat berechnet. </br>
+
Zur besseren Beurteilung der verschiedenen Berechnungsvarianten wird eine Vergleichsrechnung zwischen den historischen Methoden und den aktuellen Normen aller Welt durchgeführt. Dabei soll dargestellt werden, inwieweit sich die verschiedenen Annäherungsformeln mit denen aus dem Eurocode und der FE-Berechnung decken und welche Abweichungen es gibt. Es wird jeweils das Innenfeld eines Durchlaufträgers von Plattenbalken mit unterschiedlichen Abmessungen des normalen Hochbaus betrachtet, der mit einer konstanten Streckenlast belastet wird. Beim Vergleich der Ergebnisse wird die bezogene mitwirkende Plattenbreite <math>\cfrac{b_{eff}}{b}</math> (y-Achse) dem Verhältnis zwischen der maximalen Plattenbreite zur Stützweite <math>\cfrac{b}{l_{eff}}</math> (x-Achse) gegenübergestellt. Da nicht jede Norm <math>l_0</math> als Anhaltspunkt für die Berechnung enthält, werden die Momentennulldurchgänge für die jeweiligen Fälle separat berechnet. </br>
−
Die Querschnitt ergeben sich aus den dimensionslosen Parametern <math>\cfrac{l_{eff}}{h}</math>, <math>\cfrac{b_w}{h}</math> und <math>\cfrac{h_f}{h}</math>. Auf diese Weise können möglichst viele Parameter innerhalb einer Berechnung berücksichtigt werden und Fehler würden deutlicher abzulesen sein. Die drei betrachteten Querschnitte haben folgende Abmessungen:  
+
Die Querschnittsabmessungen ergeben sich aus den dimensionslosen Parametern <math>\cfrac{l_{eff}}{h}</math>, <math>\cfrac{b_w}{h}</math> und <math>\cfrac{h_f}{h}</math>. Auf diese Weise können möglichst viele Parameter innerhalb einer Berechnung berücksichtigt werden und Fehler würden deutlicher abzulesen sein. Für die nach FE-Methode wurde eine Forschungsarbeit von ''Utku und Aygar'' genutzt. <ref> Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings) </ref>
 +
<br /> Die drei betrachteten Querschnitte haben folgende Abmessungen:  
  
 
{| class="wikitable"
 
{| class="wikitable"
Zeile 89: Zeile 148:
 
|}
 
|}
  
−
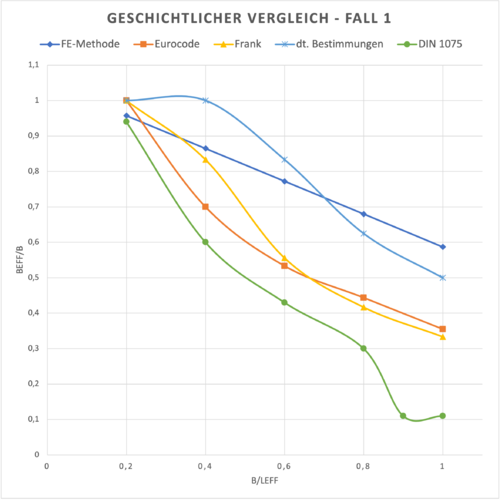
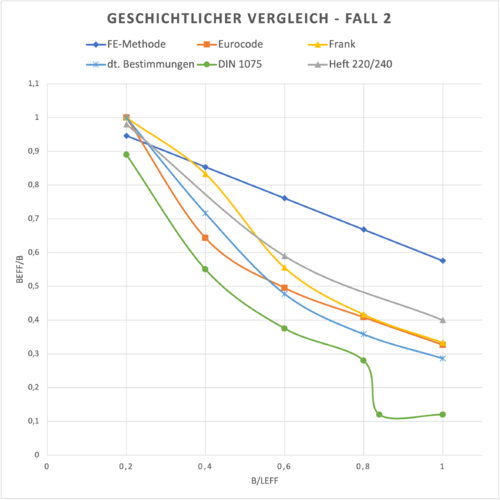
===Geschichtlicher Vergleich===
+
===Vergleich Eurocode/FE-Berechnung mit historischen Regelungen===
 +
<gallery widths=500px heights=500px>
 +
File:Mitwirkende Plattenbreite - Vergleichsrechnung 3.png|Geschichtlicher Vergleich - Fall 1: (<math>l_{eff}/h = 10</math>; <math>b_{w}/h = 0,75</math>; <math>h_{f}/h = 0,4</math>)
 +
File:Mitwirkende Plattenbreite - Vergleichsrechnung 4.png|Geschichtlicher Vergleich - Fall 2: (<math>l_{eff}/h = 15</math>; <math>b_{w}/h = 0,70</math>; <math>h_{f}/h = 0,3</math>)
 +
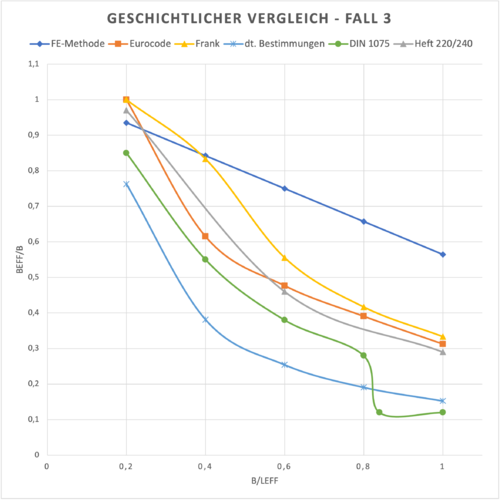
File:Mitwirkende Plattenbreite - Vergleichsrechnung 5.png|Geschichtlicher Vergleich - Fall 3: (<math>l_{eff}/h = 20</math>; <math>b_{w}/h = 0,65</math>; <math>h_{f}/h = 0,2</math>)
 +
</gallery>
 +
 
 +
===Vergleich Eurocode/FE-Berechnung mit aktuellen Normen===
 +
<gallery widths=500px heights=500px>
 +
File:Mitwirkende Plattenbreite - Vergleichsrechnung 6.png|Aktueller Vergleich - Fall 1: (<math>l_{eff}/h = 10</math>; <math>b_{w}/h = 0,75</math>; <math>h_{f}/h = 0,4</math>)
 +
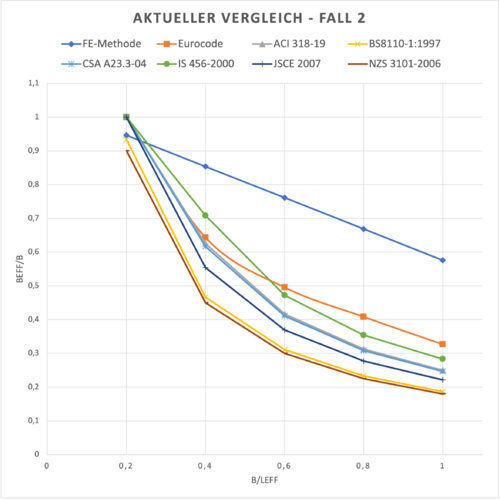
File:Mitwirkende Plattenbreite - Vergleichsrechnung 7.png|Aktueller Vergleich - Fall 2: (<math>l_{eff}/h = 15</math>; <math>b_{w}/h = 0,70</math>; <math>h_{f}/h = 0,3</math>)
 +
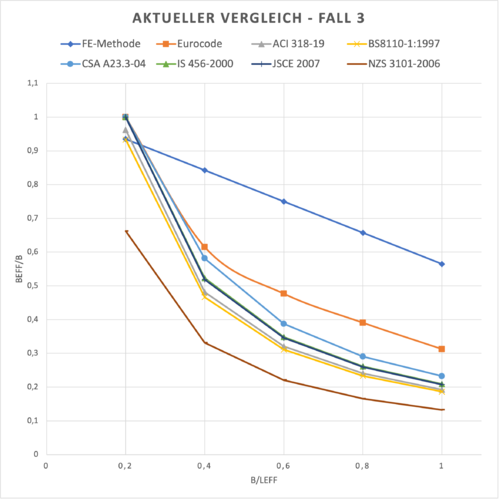
File:Mitwirkende Plattenbreite - Vergleichsrechnung 8.png|Aktueller Vergleich - Fall 3: (<math>l_{eff}/h = 20</math>; <math>b_{w}/h = 0,65</math>; <math>h_{f}/h = 0,2</math>)
 +
</gallery>
 +
 
 +
===Auswertung===
 +
Die Auswertung der Vergleichsberechnungen ergibt, dass die Regelungen nach aktuellen Normen bis auf kleine Ausnahmen gegenüber der FE-Berechnung sehr auf der sicheren Seite liegen. Die Ergebnisse der Normen unterscheiden sich selbst nur wenig voneinander, liegen jedoch auch verglichen zum Eurocode sehr auf der sicheren Seite. <br />
 +
====Zahlenbeispiel====
 +
Als Beispiel wird der Unterschied der Bewehrungsmenge für einen symmetrischen Plattenbalken (Fall 3) als Einfeldträger zwischen dem Eurocode und der NZS-Norm berechnet. Als Belastung wird 1000kNm angenommen.  <br />
 +
Querschnitt und System: <br />
 +
:<math>l_{eff} = 1000 cm</math><br />
 +
:<math>b_w = 32,5 cm</math><br />
 +
:<math> h_f = 10 cm</math><br />
 +
:<math> h = 50 cm</math><br />
 +
:<math>l_0 = 700 cm</math><br />
 +
:<math>b = 600 cm</math><br />
  
  
−
===Vergleich aktueller Normen===
+
Eurocode: </br>
 +
:<math>b_{eff} = 286 cm</math><br />
 +
:<math>\mu_{Eds}=\cfrac{M_{Eds}}{b_{eff} \cdot d^2 \cdot f_{cd}}</math> </br>
 +
:<math>\mu_{Eds}=\cfrac{100000kNcm}{286cm \cdot 44cm^2 \cdot 1,7kN/cm^2}</math> </br>
 +
:<math>\mu_{Eds}=0,106</math> </br>
 +
:<math>b_{eff}/b_w = 8,8</math> </br>
 +
:<math>h_{f}/d = 0,2</math> </br>
 +
:<math>\omega = 0,1108</math> </br>
 +
:<math>A_{s}=\cfrac{1}{f_{yd}} (\omega \cdot b_{eff} \cdot d \cdot f_{cd} )</math> </br>
 +
:<math>A_{s}=\cfrac{1}{43,5} (0,1108 \cdot 286cm \cdot 44cm \cdot 1,7kN/cm^2 )</math> </br>
 +
:<math>A_{s}=54,5cm^2</math> </br>
  
 +
NZS: </br>
 +
:<math>b_{eff} = 132,5 cm</math><br />
 +
:<math>\mu_{Eds}=\cfrac{M_{Eds}}{b_{eff} \cdot d^2 \cdot f_{cd}}</math> </br>
 +
:<math>\mu_{Eds}=\cfrac{100000kNcm}{132,5cm \cdot 44cm^2 \cdot 1,7kN/cm^2}</math> </br>
 +
:<math>\mu_{Eds}=0,23</math> </br>
 +
:<math>b_{eff}/b_w = 4</math> </br>
 +
:<math>h_{f}/d = 0,2</math> </br>
 +
:<math>\omega = 0,234</math> </br>
 +
:<math>A_{s}=\cfrac{1}{f_{yd}} (\omega \cdot b_{eff} \cdot d \cdot f_{cd} )</math> </br>
 +
:<math>A_{s}=\cfrac{1}{43,5} (0,234 \cdot 135cm \cdot 44cm \cdot 1,7kN/cm^2 )</math> </br>
 +
:<math>A_{s}=54,3cm^2</math> </br>
  
 +
Vergleich: Die Längsbewehrung in der Biegezugzone würde nach beiden Normen etwa dasselbe Ergebnis ergeben. Der große Unterschied zwischen den Ergebnissen ist, dass nach der neuseeländischen Norm zusätzlich eine Bewehrung in der Biegedruckzone nötig wird.
  
 
==Quellen==
 
==Quellen==

Aktuelle Version vom 12. Dezember 2022, 19:05 Uhr

Historische Abbildung zur Berechnung der mitwirkenden Plattenbreite aus [1]

Diese Seite zeigt die Zusammenfassung der geschichtlichen Entwicklung der mitwirkenden Plattenbreite sowie den Vergleich zwischen den Berechnungsmethoden des letzten Jahrhunderts und dem dem Eurocode. Zusätzlich werden Berechnungsvarianten aus Normen außerhalb des Eurocodes und eine FE-Berechnung vorgestellt und verglichen.


Geschichtliche Entwicklung bis zum Eurocode

Die folgende Auflistung gibt einen kurzen Überblick über die geschichtlichen Entwicklung zur Berechnung der mitwirkenden Plattenbreite. Für eine Übersicht zur Problematik un zu den Berechnungsgrundlagen - siehe Mitwirkende Plattenbreite.


1906

Erste Erwähnung im "Eisenbetonbau" als anwendbarer Leitsatz nach Mörsch [2]

wobei:

beff... Mitwirkende Plattenbreite
leff... Effektive Stützweite

1918

Erste Normung innerhalb der 1918 veröffentlichten "Deutschen Industrie Norm" nach Frank. In der Norm ist nicht geregelt, für welchen Fall man welche Formel wählt. Es handelt sich um grobe, unbegründete Abschätzungen. [3]

wobei:

beff... Mitwirkende Plattenbreite
leff... Effektive Stützweite
b... Tatsächlich vorhandene Plattenbreite

1943

Timoshenko's Elastizitätstheorie führt zur "strengen Theorie des Plattenbalkens", die mittels AIRYscher Spannungsfunktion berechnet werden kann. Die Berechnung ist jedoch sehr umständlich, daher gelten fortan die deutschen Bestimmungen nach Schleicher [4]


wobei:

beff... Mitwirkende Plattenbreite
leff... Effektive Stützweite
bw... Stegbreite
bs... Breite der Vouten
hf... Plattendicke
b... Tatsächlich vorhandene Plattenbreite

1960

Brendel fasst im Jahr 1960 das Wissen um die mitwirkende Plattenbreite kompakt zusammen. Der Fachartikel "Die mitwirkende Plattenbreite nach Theorie und Versuch" ist noch heute von großer Bedeutung. Lässt man FE-Methoden außen vor, sind die Betrachtungen aus 1960 in Kombination mit den sich darauf beziehenden Untersuchungen von Leonhardt die umfassendsten Näherungen. So lässt sich die bezogenen mitwirkende Plattenbreite () über die Verhältnisse und bestimmen.


wobei:

beff... Mitwirkende Plattenbreite
bw... Stegbreite
bi... Tatsächlich vorhandene einseitige Plattenbreite
b... Tatsächlich vorhandene Plattenbreite

Bestimmung der bezogenen mitwirkenden Plattenbreite [5]

Hieraus ergibt sich dann mithilfe der Tabelle der bezogenen mitwirkenden Plattenbreite, die angenäherte mitwirkende Plattenbreite. Über die Berücksichtigung der Plattendicke wird hier auch die Biegesteifigkeit der Platte einbezogen. Zudem wird mittels l0 die Art des Systems in Form der Momentennulldurchgänge einberechnet.
Auch einschnürungserzeugende Einzellasten werden erstmals über einen Abminderungsfaktor η berücksichtigt. Aus der Tabelle ist abzulesen, dass die Einschnürung vor allem bei kleinen Stützweiten einen Einfluss hat und abgemindert werden muss. [6] [7] Je größer die Stützweite im Verhältnis zur Plattenbreite ist, desto kleiner ist der zu berücksichtigende Einfluss der Einschnürung. Dieses Tragverhalten wird später auch von Schleeh anhand von Vergleichsberechnungen genauer erklärt und belegt. [8]

Abminderungsfaktor η für konzentrierte Einzellasten
bi / l0 2,0 1,0 0,8 0,6 0,4 0,2 0,1
η 0,6 0,61 0,62 0,63 0,65 0,7 0,9

1978

Bestimmung der bezogenen mitwirkenden Breite im Stützbereich(S) und Feldbereich(F) nach DIN 1075 (angelehnt an Grasser)

In der DIN 1075 für Betonbrücken aus dem Jahr 1978 ist die Elastizitätstheorie Grundlage der Berechnung. Der Plattenbalken wird demnach in Platte und Balken unterteilt. Dabei wird die Annahme getroffen, dass an den Verbindungsstellen zwischen Platte und Balkenwerden nur Schubkräfte übertragen werden können. [9] Diese Längsdruckspannungen nehmen dann nach Scheibentheorie mit Abstand zum Balken ab. Die DIN 1075 unterscheidet dabei zwei Fälle:

1. -> Die Platte darf über die gesamte Breite als mittragend angesetzt werden.
2. -> Ermittlung der mittragenden Plattenbreite mittels folgender Formel:
wobei:
... Beiwert für den Feldbereich (siehe Diagramm)
b... Tatsächlich vorhandene Plattenbreite

1980 - heute

Ab 1980 machen vor allem die computergestützten Berechnungsmethoden mittels finiten Elementen große Fortschritte. Auch hier handelt es sich bei den bisher vorliegenden Berechnungen um Annäherungen, da verschiedene Einflussfaktoren, wie der Einfluss der Bewehrung und Rissbildung, dabei nicht berücksichtigt werden. Die FE-Berechnungen sind dabei sehr genau und kommen vor allem bei Sonderbauten zum Einsatz. [10] [11]


Berechnung außerhalb des Eurocodes

Die Regeln zur Berechnung der mitwirkenden Plattenbreite variieren in den Normen der verschiedenen Ländern der Welt. Viele orientieren sich dabei am Eurocode, einige am ACI, andere Länder nutzen veraltete Näherungsmethoden. Folgend sollen einige aktuelle Formeln aus Normen aller Welt vorgestellt werden.

USA – ACI 318-19 [12]

Canada – CSA A23.3-04 [13]

Neuseeland – NZS 3101-2006 [14]

Großbritannien – BS 8110-1:1997 [15]

Indien – IS 456-2000 [16]

Japan – JSCE 2007 [17]


Vergleichsrechnungen

Methodik

Zur besseren Beurteilung der verschiedenen Berechnungsvarianten wird eine Vergleichsrechnung zwischen den historischen Methoden und den aktuellen Normen aller Welt durchgeführt. Dabei soll dargestellt werden, inwieweit sich die verschiedenen Annäherungsformeln mit denen aus dem Eurocode und der FE-Berechnung decken und welche Abweichungen es gibt. Es wird jeweils das Innenfeld eines Durchlaufträgers von Plattenbalken mit unterschiedlichen Abmessungen des normalen Hochbaus betrachtet, der mit einer konstanten Streckenlast belastet wird. Beim Vergleich der Ergebnisse wird die bezogene mitwirkende Plattenbreite (y-Achse) dem Verhältnis zwischen der maximalen Plattenbreite zur Stützweite (x-Achse) gegenübergestellt. Da nicht jede Norm als Anhaltspunkt für die Berechnung enthält, werden die Momentennulldurchgänge für die jeweiligen Fälle separat berechnet.
Die Querschnittsabmessungen ergeben sich aus den dimensionslosen Parametern , und . Auf diese Weise können möglichst viele Parameter innerhalb einer Berechnung berücksichtigt werden und Fehler würden deutlicher abzulesen sein. Für die nach FE-Methode wurde eine Forschungsarbeit von Utku und Aygar genutzt. [18]
Die drei betrachteten Querschnitte haben folgende Abmessungen:

Abmessungen der Querschnitte
Fall Q1 Q2 Q3
10 15 20
0,75 0,7 0,65
0,4 0,3 0,2

Vergleich Eurocode/FE-Berechnung mit historischen Regelungen

  • Geschichtlicher Vergleich - Fall 1: (; ; )

  • Geschichtlicher Vergleich - Fall 2: (; ; )

  • Geschichtlicher Vergleich - Fall 3: (; ; )

Vergleich Eurocode/FE-Berechnung mit aktuellen Normen

  • Aktueller Vergleich - Fall 1: (; ; )

  • Aktueller Vergleich - Fall 2: (; ; )

  • Aktueller Vergleich - Fall 3: (; ; )

Auswertung

Die Auswertung der Vergleichsberechnungen ergibt, dass die Regelungen nach aktuellen Normen bis auf kleine Ausnahmen gegenüber der FE-Berechnung sehr auf der sicheren Seite liegen. Die Ergebnisse der Normen unterscheiden sich selbst nur wenig voneinander, liegen jedoch auch verglichen zum Eurocode sehr auf der sicheren Seite.

Zahlenbeispiel

Als Beispiel wird der Unterschied der Bewehrungsmenge für einen symmetrischen Plattenbalken (Fall 3) als Einfeldträger zwischen dem Eurocode und der NZS-Norm berechnet. Als Belastung wird 1000kNm angenommen.
Querschnitt und System:








Eurocode:











NZS:











Vergleich: Die Längsbewehrung in der Biegezugzone würde nach beiden Normen etwa dasselbe Ergebnis ergeben. Der große Unterschied zwischen den Ergebnissen ist, dass nach der neuseeländischen Norm zusätzlich eine Bewehrung in der Biegedruckzone nötig wird.

Quellen

  1. ↑ Pucher, A: Lehrbuch des Stahlbetonbaues - Grundlagen und Anwendungen im Hoch- und Brückenbau
  2. ↑ Mörsch E.: Der Eisenbetonbau: Seine Theorie und Anwendung. Stuttgart, 1906
  3. ↑ Frank, W.: Eisenbetonbau: Kurzgefasstes Lehrbuch unter besonderer Berücksichtigung der Bedürfnisse der Praxis. 2. vollständig umgearbeitete Auflage. Stuttgart : Verlag von Konrad Wittwer, 1914
  4. ↑ Schleicher, Ferdinand: Taschenbuch für Bauingenieure. Berlin, Heidelberg : Springer Berlin Heidelberg, 1955. – ISBN 978–3–642–88349–1
  5. ↑ Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6
  6. ↑ Brendel, G.: Die mitwirkende Plattenbreite nach Theorie und Versuch. In: Beton- und Stahlbetonbau 55 (1960), Nr. 8, S. 177–185. – ISSN 00059900
  7. ↑ Leonhardt, Fritz ; Mönnig, Eduard: Vorlesungen über Massivbau. Berlin, Heidelberg : Springer Berlin Heidelberg, 1973. – ISBN 978–3–540–06488–6
  8. ↑ Schleeh, W.: Die mitwirkende Plattenbreite aus der Sicht neuer Erkenntnisse. In: Beton- und Stahlbetonbau 68 (1973), Nr. 7, S. 175–179. – ISSN 00059900
  9. ↑ Grasser, E. ; Moosecker, W.: Hilfsmittel zur näherungsweisen Bestimmung der mitwirkenden Breite von Plattenbalken im Stahlbetonbau. In: Beton- und Stahlbetonbau 77 (1982), Nr. 6, S. 164–167. – ISSN 00059900
  10. ↑ Loo, Y.-C ; Sutani ; T.D.: Effective flange width formulas for T-beams. In: Concrete International. Design and Construction 8 (1986), Nr. 2, S. 40–45
  11. ↑ Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)
  12. ↑ ACI 318-19: Building Code Requirements for Structural Concrete. American Concrete Institute
  13. ↑ CSA A23.3-04: Design of concrete structures. Mississauga, Ont. : Canadian Standard Association, 2004 (CSA standard). – ISBN 1–55397–559–6
  14. ↑ NZS 3101.1&2:2006: Concrete Structures Standard - Code of Practise for the Design of Concrete Structures. Wellington, 2006
  15. ↑ BS 8110-1:1997: Structural use of concrete. Code of practice for design and construction. 2nd ed. London : British Standards Institution, 2007 (British standard). – ISBN 9780580598937
  16. ↑ IS 456:2000 Indian Standard: Plain and Reinforced Concrete - Code of Practise. New Delhi : Bureau of Indian Standards, 2007
  17. ↑ JSCE 2007:15: Standard Specifications for Concrete Structures: "Design". To- kio : Japan Society of Civil Engineers, 2010
  18. ↑ Utku, M. ; Aygar, A.: Investigation of Effective Flange Width Formulas for T-Beams. In: Topping, B.H.V. (Hrsg.) ; Bittnar, Z. (Hrsg.): Proceedings of the Sixth International Conference on Computational Structures Technology, Civil-Comp PressStirlingshire, UK, 2002 (Civil-Comp Proceedings)


Seiteninfo
Quality-flag-white.gif
Status: Seite in Bearbeitung!
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Mitwirkende_Plattenbreite_-_Vergleichsrechnung&oldid=13220“