Brandschutznachweis Stahlbetonstütze (Bsp.): Unterschied zwischen den Versionen

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen
 
(122 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
== Methode A (Tafel) ==
+
Ein Beispiel für die Berechnung einer Stahlbeton-Innenstütze mit der [[Heißbemessung Stahlbetonbau#Methode A|Methode A]] des vereinfachten Verfahrens.
−
=== Gegeben: ===
 
−
Stahlbetonpendelstütze:<br />
 
−
- unverschieblich<br />
 
−
- beidseitig gelenkig gelagert<br />
 
−
- Nutzung als Verkaufsraum<br />
 
−
- allseitig beflammt<br />
 
−
- gefordert: R60<br />
 
  
−
=== Einwirkungen ===
+
==Aufgabenstellung==
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 1.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
+
{| style="float:right;"
−
<br />
+
| [[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.).png|350px|rechts]]||[[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.)2.png|200px|rechts]]||[[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.)3.png|250px|rechts]]
 +
|}
 +
===Gegeben===
 +
* eine Stahlbeton-Innenstütze in einem ausgesteiften Bauwerk
 +
* Kopf und Fuß der Stütze sind rotationsbehindert (eingespannt)
 +
* l = 4m
 +
* h/b = 300/300mm
 +
* N<sub>Ed</sub> = 400kN
 +
* vorhandene Bewehrung: 4Ø12 Längsbewehrung;  Ø8 Bügelbewehrung alle 14 cm; A<sub>s,vorh</sub> = 4,52 cm<sup>2</sup>
  
−
=== Querschnitts- und Systemabmessungen ===
+
===Gefordert===
 +
Für die Stahlbeton-Innenstütze wird eine Feuerwiderstandsdauer für 60 Minuten unter einer mehrseitigen Brandbeanspruchung gefordert.
  
−
<math>\begin{array}{l}b/h=30/30\\l=3m\\\frac{{{d}_{1}}}{h}=\frac{0,054}{0,3}=0,18\approx 0,2\end{array}</math>
+
==Nachweis mit der Tabelle 5.2a der [[Heißbemessung Stahlbetonbau#Methode A|Methode A]]==
  
−
auf sichere Seite gerundet
+
===Randbedingungen<ref name="EC2">DIN EN 1992-1-2:2010-12: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-2: Allgemeine Regeln – Tragwerksbemessung für den Brandfall.</ref>===
  
−
=== Schnittgrößen ===
+
*'''Ersatzlänge der Stütze im Brandfall'''
 +
::{|
 +
| || <math>{{l}_{0,fi}}  \leq 3m</math>
 +
|-
 +
| || Da der Kopf und der Fuß der Stütze rotationsbehindert gelagert sind, ergibt sich die [[Heißbemessung Stahlbetonbau#Einspannung von Pendelstützen im Brandfall| Knicklänge für den Brandfall für eine Innenstütze]] mit:
 +
|-
 +
| || <math>{{l}_{0,fi}}  = 0,5 \cdot l = 0,5 \cdot 4m = 2m</math>
 +
|-
 +
| || → Die Randbedingung ist mit 2m ≤ 3m erfüllt.
 +
|}
  
−
<math>\begin{array}{l}{{N}_{Ed}}=1,35\cdot 400+1,5\cdot 200=840kN\\{{M}_{Ed}}=66,3kNm\end{array}</math>
+
*'''Bewehrungsgehalt ρ'''
−
<br /><br />
+
::{|
−
ohne Rechnung, einschließlich Theorie II. Ordnung
+
| || <math>\rho = \frac{{{4,52 cm^2}}}{{{30 cm \cdot 30 cm}}} = 0,5 % \leq 4 %</math>
 +
|-
 +
| || → Die Randbedingung ist erfüllt.
 +
|}
  
−
=== Kaltbemessung ===
+
===Schnittgrößen<ref name="Brandschutz EU">Dietmar Hosser; Jochen Zehfuß (Hrsg.): Brandschutz in Europa - Bemessung nach Eurocodes - 3., Überarbeitete und erweiterte Auflage 2017</ref>===
−
==== Bezogene Schnittgrößen ====
+
*'''Tragfähigkeit der Stütze bei Normaltemperatur'''
 +
::{|
 +
| || <math>{{N}_{Ed,fi,t}} = {{\eta }_{fi}} \cdot {{N}_{Ed}} = 0,7 \cdot (-400 kN) = -280 kN</math>
 +
|-
 +
| || <math>{{N}_{Rd}} \approx {{N }_{ED}} = -400 kN</math>
 +
|}
  
−
<math>\begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-840}{30\cdot 30\cdot 0,85\cdot \frac{2,0}{1,5}}=-0,82\\{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{6630}{30\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,0}{1,5}}=0,22\end{array}</math>
+
*'''Lastausnutzungsfaktor μ<sub>fi</sub>'''
 +
::{|
 +
| || <math>{{\mu }_{fi}} =\frac{{{N}_{Ed,fi,t}}}{{{N}_{Rd}}} = \frac{{{-280 kN}}}{{{-400 kN}}} = 0,7</math>
 +
|}
  
−
==== Interaktionsdiagramm ====
+
===erforderliche Querschnittsabmessungen nach der Tabelle 5.2a<ref name="Brandschutz EU" />===
−
Ermittlung des mechanischen Bewehrungsgrades, <math>{{\omega }_{tot}}=0,56~</math>
+
[[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.)4.png|mini|500px|rechts]]
 +
::{|
 +
| || b<sub>min.</sub> = 250mm
 +
|-
 +
| || a<sub>erf.</sub> = 46mm
 +
|}
  
−
<math>{{A}_{s}}={{\omega }_{tot}}\cdot \frac{b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}=0,56\cdot \frac{0,3\cdot 0,3}{\frac{50}{1,15}/\left( 0,85\cdot \frac{2}{1,5} \right)}=13,09cm{}^\text{2}</math>
+
===vorhandene Querschnittsabmessungen===
 +
::{|
 +
| || b<sub>vorh.</sub> = 300mm
 +
|-
 +
| || a<sub>vorh.</sub> = 50mm
 +
|}
  
−
gewählt: 2x 6ø12, <math>{{A}_{s}}=13,57cm{}^\text{2}~</math>
+
===Ergebnis===
 +
Da die vorhandenen Querschnittsabmessungen den erforderlichen Abmessungen für die Feuerwiderstandsklasse R60 entsprechen, kann die Stahlbeton-Innenstütze der Klasse R60 zugeordnet werden.
  
−
=== Heißbemessung ===
+
===vergleichende Berechnung mit mB Baustatik===
−
==== Bedingungen ====
+
[[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.)5.png|mini|700px|zentriert]]
  
−
- Bewehrungsgrad <math>\frac{13,57}{30\cdot 30}=0,015\le 0,04</math><br />
+
Auch nach der Berechnung mit mB Baustatik kann die Stahlbeton-Innenstütze der Feuerwiderstandsklasse R60 zugeordnet werden.
−
- <math>{{l}_{0,fi}}=3\le 3</math>
 
−
<br /><br />
 
−
Bemessung nach Tafel legitimiert.
 
  
−
==== Außergewöhnliche Einwirkungskombination während des Brandfalls ====
+
==Nachweis mit der Gleichung 5.7 der [[Heißbemessung Stahlbetonbau#Methode A|Methode A]]==
  
−
<math>{{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN</math>
+
===Randbedingungen<ref name="Brandschutz EU" />===
 +
*'''Achsabstand a der Längsbewehrung''':
 +
::{|
 +
| || <math>25mm \leq a \leq 80mm </math>
 +
|-
 +
| || <math>a = 50mm </math>
 +
|-
 +
| || → Randbedingung erfüllt.
 +
|}
  
−
==== Ermittlung des Reduktionsfaktors ====
+
* '''Ersatzstablänge im Brandfall''':
 +
::{|
 +
| || <math> {{l}_{0,fi}} \leq 6m </math>
 +
|-
 +
| || <math> {{l}_{0,fi}} = 2m </math>
 +
|-
 +
| || → Randbedingung erfüllt.
 +
|}
  
−
<math>{{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62</math>
+
*'''b`'''
 +
::{|
 +
| || <math>200mm \leq b\prime \leq 450mm </math>
 +
|-
 +
| || <math>200mm \leq \frac{{{(2\cdot Ac)}}}{{{(b+h)}}} \leq 450mm</math>
 +
|-
 +
| || <math>200mm \leq \frac{{{(2\cdot300^2)}}}{{{(300+300)}}} \leq 450mm</math>
 +
|-
 +
| || <math>200mm \leq 300mm \leq 450mm </math>
 +
|-
 +
| || → Randbedingung erfüllt.
 +
|}
  
−
==== Bezogene Schnittgrößen ====
+
*'''Querschnittshöhe'''
−
(vereinfacht mit <math>0,62\cdot {{\nu }_{Ed}}</math> oder genauer mit <math>{{\alpha }_{cc}}=1,0~</math>):
+
::{|
 +
| || <math> h \leq 1,5\cdot b </math>
 +
|-
 +
| || <math>300mm \leq 1,5\cdot300mm </math>
 +
|-
 +
| || <math>300mm \leq 450mm </math>
 +
|-
 +
| || → Randbedingung erfüllt.
 +
|}
  
−
<math>\begin{array}{l}{{\nu }_{Ed,fi,t}}=\frac{{{N}_{Ed,fi}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-520}{30\cdot 30\cdot \frac{2,0}{1,5}}=-0,43\\{{\mu }_{Ed,fi,t}}=\frac{{{M}_{Ed,fi}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{0,62\cdot 6630}{30\cdot 30{}^\text{2}\cdot \frac{2,0}{1,5}}=0,11\end{array}</math>
+
===Gleichung 5.7<ref name="Brandschutz EU" />===
  
−
==== Mechanischer Bewehrungsgrad ====
+
::<math>R=120\cdot {{\left( \frac{{{R}_{\eta fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}</math>
−
bei Berücksichtigung von <math>{{\alpha }_{cc}}=1,0~</math>:
 
  
−
<math>{{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/\frac{2,0}{1,5} \right)}{30\cdot 30}=0,49</math>
+
===Ermittlung der Einflussfaktoren<ref name="Brandschutz EU" />===
 +
*'''mit:'''
 +
::{|
 +
|<math>{{\eta}_{fi}}= 0,7</math> || Ausnutzungsgrad
 +
|-
 +
| <math> n = 4</math> || Anzahl der Bewehrungsstäbe
 +
|-
 +
|<math>{{\alpha}_{cc}}= 0,85</math> || Dauerstandfestigkeit nach DIN EN 1992-1-1
 +
|-
 +
|<math>{\omega}=\frac{{{A}_{s}\cdot{f}_{yd}}}{{{A}_{c}\cdot{f}_{cd}}} = \frac{{{4,52}\cdot \frac{{{50}}}{{{1,15}}} }}{{{30^2}\cdot \frac{{{2,0}}}{{{1,5}}} }} = 0,193</math> || mechanischer Bewehrungsgrad
 +
|}
  
−
==== Ermittlung der zulässigen bezogenen Normalkraft mithilfe des Interaktionsdiagramms ====
+
*'''Einfluss des Lastniveaus'''
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 2.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
+
::<math>{R_{\eta fi}}=83\cdot \left( 1-{{\mu }_{fi}}\cdot \frac{(1+\omega )}{(0,85/{{\alpha }_{cc}})+\omega } \right)</math>  
−
<br />
+
::<math>{R_{\eta fi}}=83\cdot (1-0,7\cdot\frac{{{1+0,193}}}{{{1+0,193}}}=24,9</math>  
  
−
Vom Diagrammnullpunkt über den Schnittpunkt der bezogenen heißbemessenen Schnittgrößen wird der mechanische Bewehrungsgrad angezielt und damit
+
*'''Einfluss des Achsabstandes'''
−
<math>{{\nu }_{Ed,fi,t,zul}}=-0,79~</math> abgelesen.<br />
+
::<math>{R_{a}}=1,6\cdot (a-30)</math>  
−
Der Bemessungswiderstand der Normalkraft ergibt sich durch Wiedereinführen der Abmessungen:
+
::<math>{R_{a}}=1,6\cdot(50-30)=32</math>  
  
−
<math>{{N}_{Rd}}={{\nu }_{Ed,fi,t,zul}}\cdot b\cdot h\cdot {{f}_{cd}}=-0,79\cdot 30\cdot 30\cdot \frac{2}{1,5}=-948kN</math>
+
*'''Einfluss der Stützenlänge'''
 +
::<math>{R_{l}}=9,6\cdot (5-{{l}_{0,fi}})</math>
 +
::<math>{R_{l}}=9,6\cdot(5-2)=28,8</math>  
  
−
Das Verhältnis aus Einwirkung und Widerstand ergibt den Ausnutzungsgrad
+
*'''Einfluss der Querschnittsabmessungen'''
 +
::<math>{R_{b}}=0,09\cdot b'</math>
 +
::<math>{R_{b}}=0,09\cdot300=27</math>
  
−
<math>{{\mu }_{fi}}=\frac{{{N}_{Ed,fi,t}}}{{{N}_{Rd}}}=\frac{-520}{-948}=0,55</math>
+
*'''Einfluss der Bewehrung'''
 +
::<math>{R_{n}}=0\quad  f\ddot{u}r\quad n=4 </math>
  
−
Durch Interpolation ergeben sich in der Tafel des Eurocode 2 für Methode A mit geforderter Brandwiderstandsdauer von 60 Minuten die folgenden Mindestabmessungen und Achsabstände:<br /><br />
+
===Ergebnis der Berechnung===
  
−
212,5mm/38,5mm oder 312,5mm/33,25mm
+
::<math>R=120\cdot {{\left( \frac{{24,9}+{32}+{28,8}+{27}+{0}}{120} \right)}^{1,8}}=107,18 min</math>
−
<br /><br />
 
  
−
Stütze mit 300mm/54mm eingehalten, Nachweis erfüllt.<br /><br />
+
Die Berechnung mit der Gleichung 5.7 ergibt für die Stahlbeton-Innenstütze eine Feuerwiderstandsdauer von 107,18 Minuten.
  
−
Anmerkungen:<br />
+
===Vergleichsberechnung mit mB Baustatik===
−
In der Vergleichsrechnung mit dem Modul S402.de wird die „kalte“ Einwirkungskombination mit <math>{{\gamma }_{G,\inf }}</math> , jedoch auch mit
+
[[Datei:Brandschutznachweis Stahlbetonstütze (Bsp.)6.png|700px|gerahmt|center]]
−
<math>{{\gamma }_{Q,\sup }}</math>  berechnet. Weiterhin ist der Bemessungswert der „heißen“ Einwirkungskombination nicht nachzuvollziehen. Als Konsequenz ergibt sich ein höherer Ausnutzungsfaktor und eine entsprechend höhere Forderung zum Einhalten der Forderung R60.<br />
+
Die Berechnung der Stahlbeton-Innenstütze mit mB Baustatik ergibt eine Feuerwiderstandsdauer von 164,9 Minuten. Damit kann die Stütze sogar der Feuerwiderstandsklasse R120 zugeordnet werden.
−
Eine Nachweisführung mit Methode B kann in diesem Fall nicht erfolgen, weil die Stütze eine Schlankheit von 30 als Bedingung übersteigt.
 
  
−
=== mb-Vergleichsrechnung ===
+
==Beurteilung der Ergebnisse==
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 3.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
+
Die Stahlbeton-Innenstütze kann sowohl nach der Berechnung mit der Tabellen 5.2a, als auch nach der Berechnung mit der Gleichung 5.7, einer Feuerwiderstandsdauer von mindestens 60 Minuten zugeordnet werden.
−
<br />
 
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 4.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
 
−
<br />
 
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 5.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
 
−
<br />
 
  
−
== Methode A (Gleichung) ==
+
Die Berechnung mit der Tabelle 5.2a gestaltet sich dabei als die einfachere Variante. Nach der Prüfung der Randbedingungen und der Berechnung des Lastausnutzungsfaktors, können die erforderlichen Querschnittsabmessungen für die benötigte Feuerwiderstandsdauer aus der Tabelle 5.2a abgelesen werden.  
−
Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A).<br />
 
−
Die Vorgehensweise zu Ermittlung des Ausnutzungsgrades ist dieselbe.
 
  
−
=== Mechanischer Bewehrungsgrad ===
+
Die Berechnung nach der Gleichung 5.7 erfordert aufgrund der zusätzlichen Ermittlung der Einflussfaktoren mehr Aufwand. Allerdings ergibt sich bei dieser Methode der Vorteil, dass durch die erweiterten Randbedingungen ein größerer Anwendungsbereich ermöglicht wird, als mit der Tabelle 5.2a. Zudem ergibt das Ergebnis eine konkrete Feuerwiderstandsdauer in Minuten, wohingegen mit der Tabelle 5.2a lediglich die für eine Feuerwiderstandsdauer benötigten Querschnittsabmessungen ermittelt werden.
  
−
<math>{{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/0,85\cdot \frac{2,0}{1,5} \right)}{30\cdot 30}=0,58</math>
+
===Erläuterung der Unterschiede zwischen der Handberechnung und mB-Baustatik===
  
−
=== Ermittlung der Summanden ===
+
Bei der Handberechnung wurde zur Vereinfachung angenommen, dass die Stütze unter Normaltemperatur voll ausgelastet ist. Es gilt also N<sub>Rd</sub>=N<sub>Ed</sub>. Unter dieser Annahme wurden auch die Tabellenwerte des Tabellenverfahrens ermittelt.
  
−
<math>\begin{array}{l}{{R}_{\eta ,fi}}=83\cdot \left( 1-{{\mu }_{fi}}\cdot \frac{1+\omega }{(0,85/{{\alpha }_{cc}})+\omega } \right)=83\cdot \left( 1-0,55\cdot \frac{1+0,58}{(0,85/1)+0,58} \right)=32,56\\{{R}_{a}}=1,6\cdot (a-30)=1,6\cdot \left( 54-30 \right)=38,4\\{{R}_{l}}=9,6\cdot (5-{{l}_{0,fi}})=9,6\cdot (5-3)=19,2\\{{R}_{b}}=0,09\cdot b'=0,09\cdot \frac{2\cdot {{A}_{c}}}{b+h}=0,09\cdot \frac{2\cdot (300{}^\text{2}-1357)}{300+300}=26,59\\{{R}_{n}}=12\end{array}</math>
+
In diesem Beispiel ist es jedoch so, dass die Stütze bei Normaltemperatur nicht voll ausgelastet ist. Dies bedeutet also, dass die eigentliche Tragfähigkeit der Stütze N<sub>Rd</sub> deutlich größer ist, als in der Handberechnung bei der Berechnung des Lastausnutzungsfaktor μ<sub>fi</sub> angenommen wurde.
  
−
=== Ermittlung der Branddauer ===
+
Bei der Berechnung mit mB Baustatik wurde der Lastausnutzungsfaktor μ<sub>fi</sub> hingegen mit der vollen Tragfähigkeit der Stütze und der vollen Last N<sub>Ed</sub> = N<sub>Ed,fi</sub> berechnet. Die eigentliche Tragfähigkeit der Stütze N<sub>Rd</sub> liegt bei N<sub>Rd</sub> = 1200,96 kN. Dementsprechend ergibt sich also ein viel geringerer Lastausnutzungsfaktor, als in der Handberechnung. Dies hat zur Folge, dass die Stahlbeton-Innenstütze, nach der Berechnung mit mB Baustatik, im Brandfall deutlich länger standhalten würde. Aufgrund dessen, dass bei der Berechnung die volle Last N<sub>Ed</sub> = N<sub>Ed,fi</sub> angesetzt wird, liegt die Berechnung auf jeden Fall auf der sicheren Seite.
  
−
<math>R=120\cdot {{\left( \frac{{{R}_{\eta ,fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}=120\cdot {{\left( \frac{32,56+38,4+19,2+26,59+12}{120} \right)}^{1,8}}=136\min </math>
+
Da in der Aufgabenstellung jedoch nur eine Feuerwiderstandsdauer von 60 Minuten gefordert wurde, ist die Aufgabe dennoch auch mit der Handberechnung erfüllt. Wäre dies nicht der Fall, hätte die genaue Tragfähigkeit der Stütze bestimmt werden müssen.
−
<br /><br />
 
−
Nachweis erfüllt.
 
  
−
=== mb-Vergleichsrechnung ===
 
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 6.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
 
−
<br />
 
−
 
−
== Methode B ==
 
−
Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A). Die Länge wird hier mit <math>l=2,5m</math> vorgegeben. Das Moment nach Theorie II. Ordnung ergibt sich zu <math>{{M}_{Ed,2}}=65,25kNm~</math>.
 
−
 
−
=== Mechanischer Bewehrungsgrad ===
 
−
 
−
<math>\omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{13,57\cdot \frac{50}{1,15}}{\left( {{30}^{2}}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}}=0,59a</math>
 
−
 
−
=== Außergewöhnliche Einwirkungskombination während des Brandfalls ===
 
−
 
−
<math>{{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN</math>
 
−
 
−
=== Ermittlung des Reduktionsfaktors ===
 
−
 
−
<math>{{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62</math>
 
−
 
−
=== Ermittlung des Ausnutzungsgrades ===
 
−
 
−
<math>n=\frac{{{N}_{Ed,fi}}}{0,7\cdot \left( {{A}_{c}}\cdot {{f}_{cd}}+{{A}_{s}}\cdot {{f}_{yd}} \right)}=\frac{520}{0,7\cdot \left[ \left( 30{}^\text{2}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}+13,57\cdot \frac{50}{1,15} \right]}=0,47</math>
 
−
 
−
=== Zulässige Knicklänge ===
 
−
 
−
<math>{{\lambda }_{fi,t}}=\frac{{{l}_{0,fi}}}{i}=\frac{{{l}_{0,fi}}}{\sqrt{\frac{I}{A}}}=\frac{250}{\sqrt{\frac{{{30}^{4}}/12}{{{30}^{2}}}}}=28,87\le 30</math>
 
−
 
−
=== Zulässige Ausmitte ===
 
−
 
−
<math>e=\frac{{{M}_{0,Ed,fi}}}{{{N}_{Ed,fi}}}=\frac{0,62\cdot 65,25}{520}=0,079m>b\cdot 0,25=0,075m</math>
 
−
<br /><br />
 
−
Bedingung nicht erfüllt, ein Eingang in die Tafel ist hinfällig.
 
−
 
−
=== mb-Vergleichsrechnung ===
 
−
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 7.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br />
 
−
<br />
 
−
 
−
<br />
 
 
==Quellen==
 
==Quellen==
  

Aktuelle Version vom 25. August 2023, 15:02 Uhr

Ein Beispiel für die Berechnung einer Stahlbeton-Innenstütze mit der Methode A des vereinfachten Verfahrens.

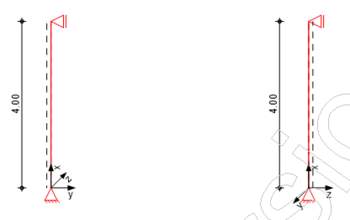
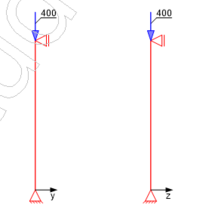
Aufgabenstellung

Brandschutznachweis Stahlbetonstütze (Bsp.).png
Brandschutznachweis Stahlbetonstütze (Bsp.)2.png
Brandschutznachweis Stahlbetonstütze (Bsp.)3.png

Gegeben

  • eine Stahlbeton-Innenstütze in einem ausgesteiften Bauwerk
  • Kopf und Fuß der Stütze sind rotationsbehindert (eingespannt)
  • l = 4m
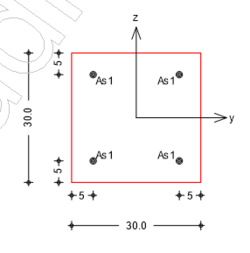
  • h/b = 300/300mm
  • NEd = 400kN
  • vorhandene Bewehrung: 4Ø12 Längsbewehrung; Ø8 Bügelbewehrung alle 14 cm; As,vorh = 4,52 cm2

Gefordert

Für die Stahlbeton-Innenstütze wird eine Feuerwiderstandsdauer für 60 Minuten unter einer mehrseitigen Brandbeanspruchung gefordert.

Nachweis mit der Tabelle 5.2a der Methode A

Randbedingungen[1]

  • Ersatzlänge der Stütze im Brandfall
Da der Kopf und der Fuß der Stütze rotationsbehindert gelagert sind, ergibt sich die Knicklänge für den Brandfall für eine Innenstütze mit:
→ Die Randbedingung ist mit 2m ≤ 3m erfüllt.
  • Bewehrungsgehalt ρ
→ Die Randbedingung ist erfüllt.

Schnittgrößen[2]

  • Tragfähigkeit der Stütze bei Normaltemperatur
  • Lastausnutzungsfaktor μfi

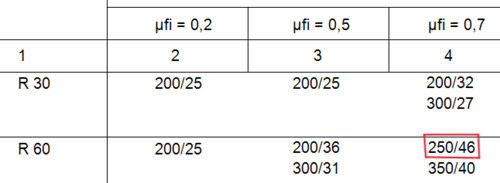
erforderliche Querschnittsabmessungen nach der Tabelle 5.2a[2]

Brandschutznachweis Stahlbetonstütze (Bsp.)4.png
bmin. = 250mm
aerf. = 46mm

vorhandene Querschnittsabmessungen

bvorh. = 300mm
avorh. = 50mm

Ergebnis

Da die vorhandenen Querschnittsabmessungen den erforderlichen Abmessungen für die Feuerwiderstandsklasse R60 entsprechen, kann die Stahlbeton-Innenstütze der Klasse R60 zugeordnet werden.

vergleichende Berechnung mit mB Baustatik

Brandschutznachweis Stahlbetonstütze (Bsp.)5.png

Auch nach der Berechnung mit mB Baustatik kann die Stahlbeton-Innenstütze der Feuerwiderstandsklasse R60 zugeordnet werden.

Nachweis mit der Gleichung 5.7 der Methode A

Randbedingungen[2]

  • Achsabstand a der Längsbewehrung:
→ Randbedingung erfüllt.
  • Ersatzstablänge im Brandfall:
→ Randbedingung erfüllt.
  • b`
→ Randbedingung erfüllt.
  • Querschnittshöhe
→ Randbedingung erfüllt.

Gleichung 5.7[2]

Ermittlung der Einflussfaktoren[2]

  • mit:
Ausnutzungsgrad
Anzahl der Bewehrungsstäbe
Dauerstandfestigkeit nach DIN EN 1992-1-1
mechanischer Bewehrungsgrad
  • Einfluss des Lastniveaus
  • Einfluss des Achsabstandes
  • Einfluss der Stützenlänge
  • Einfluss der Querschnittsabmessungen
  • Einfluss der Bewehrung

Ergebnis der Berechnung

Die Berechnung mit der Gleichung 5.7 ergibt für die Stahlbeton-Innenstütze eine Feuerwiderstandsdauer von 107,18 Minuten.

Vergleichsberechnung mit mB Baustatik

Brandschutznachweis Stahlbetonstütze (Bsp.)6.png

Die Berechnung der Stahlbeton-Innenstütze mit mB Baustatik ergibt eine Feuerwiderstandsdauer von 164,9 Minuten. Damit kann die Stütze sogar der Feuerwiderstandsklasse R120 zugeordnet werden.

Beurteilung der Ergebnisse

Die Stahlbeton-Innenstütze kann sowohl nach der Berechnung mit der Tabellen 5.2a, als auch nach der Berechnung mit der Gleichung 5.7, einer Feuerwiderstandsdauer von mindestens 60 Minuten zugeordnet werden.

Die Berechnung mit der Tabelle 5.2a gestaltet sich dabei als die einfachere Variante. Nach der Prüfung der Randbedingungen und der Berechnung des Lastausnutzungsfaktors, können die erforderlichen Querschnittsabmessungen für die benötigte Feuerwiderstandsdauer aus der Tabelle 5.2a abgelesen werden.

Die Berechnung nach der Gleichung 5.7 erfordert aufgrund der zusätzlichen Ermittlung der Einflussfaktoren mehr Aufwand. Allerdings ergibt sich bei dieser Methode der Vorteil, dass durch die erweiterten Randbedingungen ein größerer Anwendungsbereich ermöglicht wird, als mit der Tabelle 5.2a. Zudem ergibt das Ergebnis eine konkrete Feuerwiderstandsdauer in Minuten, wohingegen mit der Tabelle 5.2a lediglich die für eine Feuerwiderstandsdauer benötigten Querschnittsabmessungen ermittelt werden.

Erläuterung der Unterschiede zwischen der Handberechnung und mB-Baustatik

Bei der Handberechnung wurde zur Vereinfachung angenommen, dass die Stütze unter Normaltemperatur voll ausgelastet ist. Es gilt also NRd=NEd. Unter dieser Annahme wurden auch die Tabellenwerte des Tabellenverfahrens ermittelt.

In diesem Beispiel ist es jedoch so, dass die Stütze bei Normaltemperatur nicht voll ausgelastet ist. Dies bedeutet also, dass die eigentliche Tragfähigkeit der Stütze NRd deutlich größer ist, als in der Handberechnung bei der Berechnung des Lastausnutzungsfaktor μfi angenommen wurde.

Bei der Berechnung mit mB Baustatik wurde der Lastausnutzungsfaktor μfi hingegen mit der vollen Tragfähigkeit der Stütze und der vollen Last NEd = NEd,fi berechnet. Die eigentliche Tragfähigkeit der Stütze NRd liegt bei NRd = 1200,96 kN. Dementsprechend ergibt sich also ein viel geringerer Lastausnutzungsfaktor, als in der Handberechnung. Dies hat zur Folge, dass die Stahlbeton-Innenstütze, nach der Berechnung mit mB Baustatik, im Brandfall deutlich länger standhalten würde. Aufgrund dessen, dass bei der Berechnung die volle Last NEd = NEd,fi angesetzt wird, liegt die Berechnung auf jeden Fall auf der sicheren Seite.

Da in der Aufgabenstellung jedoch nur eine Feuerwiderstandsdauer von 60 Minuten gefordert wurde, ist die Aufgabe dennoch auch mit der Handberechnung erfüllt. Wäre dies nicht der Fall, hätte die genaue Tragfähigkeit der Stütze bestimmt werden müssen.

Quellen

  1. ↑ DIN EN 1992-1-2:2010-12: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken. Teil 1-2: Allgemeine Regeln – Tragwerksbemessung für den Brandfall.
  2. ↑ 2,0 2,1 2,2 2,3 2,4 Dietmar Hosser; Jochen Zehfuß (Hrsg.): Brandschutz in Europa - Bemessung nach Eurocodes - 3., Überarbeitete und erweiterte Auflage 2017


Seiteninfo
Quality-flag-orange.gif
Status: Seite fertig, ungeprüft
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Brandschutznachweis_Stahlbetonstütze_(Bsp.)&oldid=14418“