Zuggurtkraftdifferenz: Unterschied zwischen den Versionen
| Zeile 19: | Zeile 19: | ||
Betrachtet wird ein Stahlbetonbalken, welcher als Einfeldträger mittig durch eine Einzellast belastet wird. Aufgrund der Symmetrie genügt die Betrachtung von einer Trägerhälfte. Gekennzeichnet sind die Drehpunkte 1 und 2 für die Berechnung der Zuggurtkraft über ein Momentengleichgewicht.<ref Name = "Vorlesungsunterlagen"></ref> | Betrachtet wird ein Stahlbetonbalken, welcher als Einfeldträger mittig durch eine Einzellast belastet wird. Aufgrund der Symmetrie genügt die Betrachtung von einer Trägerhälfte. Gekennzeichnet sind die Drehpunkte 1 und 2 für die Berechnung der Zuggurtkraft über ein Momentengleichgewicht.<ref Name = "Vorlesungsunterlagen"></ref> | ||
| − | [[Datei:Zuggurtkraftdifferenz 1.png|mini|600px|none|Fachwerkmodell nach EC2-1-1]] | + | [[Datei:Zuggurtkraftdifferenz 1.png|mini|600px|none|Fachwerkmodell nach EC2-1-1]<ref Name = "Vorlesungsunterlagen"></ref>] |
Ermittelt wird die Zuggurtkraft (F<sub>s</sub>) im gekennzeichneten Betrachtungsschnitt jeweils für den Biegebalken (BB) und das Fachwerk (FW) über das Aufstellen eines Momentengleichgewichtes. | Ermittelt wird die Zuggurtkraft (F<sub>s</sub>) im gekennzeichneten Betrachtungsschnitt jeweils für den Biegebalken (BB) und das Fachwerk (FW) über das Aufstellen eines Momentengleichgewichtes. | ||
| − | [[Datei:Zuggurtkraftdifferenz 2.png|mini|600px|none|System]] | + | [[Datei:Zuggurtkraftdifferenz 2.png|mini|600px|none|System<ref Name = "Vorlesungsunterlagen"></ref>]] |
| Zeile 31: | Zeile 31: | ||
:Momentengleichgewicht um Drehpunkt 1 | :Momentengleichgewicht um Drehpunkt 1 | ||
| − | [[Datei:Zuggurtkraftdifferenz 3.png|mini|300px|right|Momentengleichgewicht um Drehpunkt 1]] | + | [[Datei:Zuggurtkraftdifferenz 3.png|mini|300px|right|Momentengleichgewicht um Drehpunkt 1<ref Name = "Vorlesungsunterlagen"></ref>]] |
::<math>0 = -F_\mathrm{s,BB}\cdot z+V_\mathrm{Ed}\cdot\cfrac{z}{2}\cdot(cot\theta+cot\alpha)</math> | ::<math>0 = -F_\mathrm{s,BB}\cdot z+V_\mathrm{Ed}\cdot\cfrac{z}{2}\cdot(cot\theta+cot\alpha)</math> | ||
| Zeile 49: | Zeile 49: | ||
:Momentengleichgewicht um Drehpunkt 2 | :Momentengleichgewicht um Drehpunkt 2 | ||
| − | [[Datei:Zuggurtkraftdifferenz 4.png|mini|300px|right|Momentengleichgewicht um Drehpunkt 2]] | + | [[Datei:Zuggurtkraftdifferenz 4.png|mini|300px|right|Momentengleichgewicht um Drehpunkt 2<ref Name = "Vorlesungsunterlagen"></ref>]] |
::<math>0 = -F_\mathrm{s,FW}\cdot z+V_\mathrm{Ed}\cdot z \cdot cot\theta</math> | ::<math>0 = -F_\mathrm{s,FW}\cdot z+V_\mathrm{Ed}\cdot z \cdot cot\theta</math> | ||
| Zeile 79: | Zeile 79: | ||
Die Zugkraft lässt sich über das am entsprechenden Betrachtungsschnitt einwirkende Biegemoment und den Hebelarm der inneren Kräfte bestimmen. Daraus lässt sich die Zugkraftlinie für das Berechnungsmodell Biegebalken Konstruieren. <ref Name = "Vorlesungsunterlagen"></ref> | Die Zugkraft lässt sich über das am entsprechenden Betrachtungsschnitt einwirkende Biegemoment und den Hebelarm der inneren Kräfte bestimmen. Daraus lässt sich die Zugkraftlinie für das Berechnungsmodell Biegebalken Konstruieren. <ref Name = "Vorlesungsunterlagen"></ref> | ||
| − | [[Datei:Zuggurtkraftdifferenz 5.png|mini|400px|none|F<sub>s</sub>-Linie aus Biegeberechnung (grüne Linie)]] | + | [[Datei:Zuggurtkraftdifferenz 5.png|mini|400px|none|F<sub>s</sub>-Linie aus Biegeberechnung (grüne Linie)<ref Name = "Vorlesungsunterlagen"></ref>]] |
===F<sub>s</sub>-Linie für Einfach Fachwerk=== | ===F<sub>s</sub>-Linie für Einfach Fachwerk=== | ||
Am Fachwerkmodell sind die Stabkräfte in den jeweiligen Bereichen der Untergurtebene jeweils konstant. Der Verlauf der Zugkraftlinie gestaltet sich somit entsprechend der Fachwerkfelder stufenförmig. | Am Fachwerkmodell sind die Stabkräfte in den jeweiligen Bereichen der Untergurtebene jeweils konstant. Der Verlauf der Zugkraftlinie gestaltet sich somit entsprechend der Fachwerkfelder stufenförmig. | ||
| − | [[Datei:Zuggurtkraftdifferenz 6.png|mini|400px|none|F<sub>s</sub>-Linie für Einfach Fachwerk (blaue Linie)]] | + | [[Datei:Zuggurtkraftdifferenz 6.png|mini|400px|none|F<sub>s</sub>-Linie für Einfach Fachwerk (blaue Linie)<ref Name = "Vorlesungsunterlagen"></ref>]] |
Projiziert man die Mittellinie eines Fachwerkfeldes abwärts auf die beiden Zugkraftlinien, lässt sich vertikal gemessen, eine Differenz feststellen. Hierbei handelt es sich um die zuvor abgeleitete Differenzkraft ΔF<sub>s</sub>. | Projiziert man die Mittellinie eines Fachwerkfeldes abwärts auf die beiden Zugkraftlinien, lässt sich vertikal gemessen, eine Differenz feststellen. Hierbei handelt es sich um die zuvor abgeleitete Differenzkraft ΔF<sub>s</sub>. | ||
| Zeile 110: | Zeile 110: | ||
Gleichermaßen lässt sich die Zugkraftlinie horizontal Parallelverschieben. Das Maß der horizontalen Verschiebung entspricht dem Versatzmaß a<sub>l</sub>. | Gleichermaßen lässt sich die Zugkraftlinie horizontal Parallelverschieben. Das Maß der horizontalen Verschiebung entspricht dem Versatzmaß a<sub>l</sub>. | ||
| − | [[Datei:Zuggurtkraftdifferenz 7.png|mini|400px|none|F<sub>s</sub>-Linie für Netzfachwerk (rote Linie)]] | + | [[Datei:Zuggurtkraftdifferenz 7.png|mini|400px|none|F<sub>s</sub>-Linie für Netzfachwerk (rote Linie)<ref Name = "Vorlesungsunterlagen"></ref>]] |
=Varianten zur Berücksichtigung der Zuggurtkraftdifferenz bei der Zugkraftdeckung= | =Varianten zur Berücksichtigung der Zuggurtkraftdifferenz bei der Zugkraftdeckung= | ||
Version vom 24. März 2024, 16:04 Uhr
Die Zuggurtkraftdifferenz ist eine von der einwirkenden Querkraft abhängige Kraftgröße. Beim Verfahren der Zugkraftdeckung ist diese zu Berücksichtigen. Die Zuggurtkraftdifferenz entsteht aufgrund der zwei unterschiedliche Berechnungsmodelle zur Ermittlung der Biegezug - und Querkraftbewehrung von Stahlbetonbauteilen.
Ursprung der Zuggurtkraftdifferenz
Beim Bemessen der Biegezug - und Querkraftbewehrung von Stahlbetonbauteilen kommen jeweils zwei unterschiedliche Berechnungsmodelle zur Anwendung. Für das Ermitteln der Biegezugbewehrung wird von der Theorie eines Biegebalkens ausgegangen, in welchem lediglich die horizontalen inneren Kräfte betrachtet werden. Hierbei werden die Berechnungen auf die Stabachse des Bauteils reduziert. Bemessen werden lediglich die maßgebenden Querschnitte (Extremstellen). Die Querkraftbemessung hingegen erfolgt auf Basis eines Fachwerkmodells, womit die gemeinsame Wirkung aus Moment und Querkraft erfasst werden kann. Die Gurtkräfte werden dabei auch in ihren realen Wirkungslinien ermittelt. Vergleicht man die Zugkraft in der Bewehrungsebene aus der Biegetheorie mit der Zuggurtkraft des Fachwerkmodells, im gleichen Betrachtungsschnitt eines Bauteils, lässt sich am Fachwerkmodell eine höhere Zugkraft feststellen. Lediglich an den Extremstellen (max MEd), also dort wo rechnerisch keine Querkräfte auftreten, stimmen die Zugkräfte beider Berechnungsmodelle überein. Vereinfacht gesagt erzeugen Querkräfte aufgrund der Fachwerktheorie zusätzliche Kräfte in der Biegezugbewehrung. Der zusätzliche Zugkraftanteil ist unter anderem von der Neigung der Druckstrebe und der Neigung der Querkraftbewehrung abhängig. Da die Berechnungen am Fachwerk realitätsnäher sind, ist die Differenzkraft beim Verfahren der Zugkraftdeckung zu berücksichtigen. Die Kräfte im Druckgurt werden infolge der Querkraft im Fachwerkmodell kleiner als nach Biegetheorie, dies wird bei der Bemessung jedoch vernachlässigt.[1]
Herleitung an einem Beispiel
In nachfolgender Beispielbetrachtung erfolgt die Ermittlung der Zuggurtkraft am Biegebalken und am Fachwerkmodell. Anhand des Gegenüberstellung beider Bestimmungsgleichungen lässt sich die Entstehung der Zuggurtkraftdifferenz verdeutlichen.
Fachwerkgeometrie und statisches System
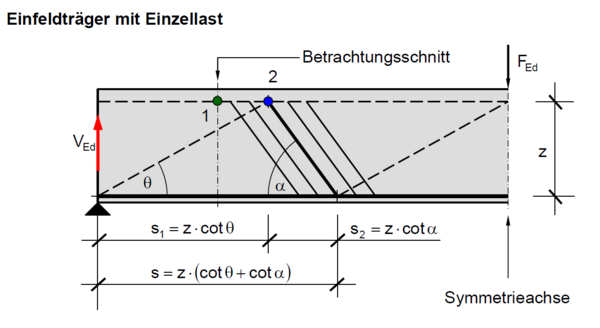
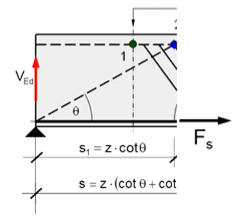
Grundlage für die Betrachtung bietet das Fachwerkmodell nach EC2-1-1, welches bei der Querkraftbemessung Anwendung findet. Die Fachwerkgeometrie ergibt sich aus dem Druckstrebenneigungswinkel θ, dem Neigungswinkel der Querkraftbewehrung α und dem Hebelarm der inneren Kräfte z. Betrachtet wird ein Stahlbetonbalken, welcher als Einfeldträger mittig durch eine Einzellast belastet wird. Aufgrund der Symmetrie genügt die Betrachtung von einer Trägerhälfte. Gekennzeichnet sind die Drehpunkte 1 und 2 für die Berechnung der Zuggurtkraft über ein Momentengleichgewicht.[1]
[[Datei:Zuggurtkraftdifferenz 1.png|mini|600px|none|Fachwerkmodell nach EC2-1-1][1]]
Ermittelt wird die Zuggurtkraft (Fs) im gekennzeichneten Betrachtungsschnitt jeweils für den Biegebalken (BB) und das Fachwerk (FW) über das Aufstellen eines Momentengleichgewichtes.
Ermittlung der Zuggurtkraft Fs
- Ermittlung von Fs am Biegebalken[1]
- Momentengleichgewicht um Drehpunkt 1
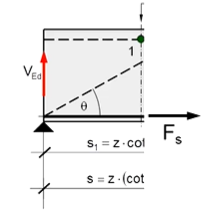
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 = -F_\mathrm{s,BB}\cdot z+V_\mathrm{Ed}\cdot\cfrac{z}{2}\cdot(cot\theta+cot\alpha)}
- ↓
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{s,BB}=\cfrac{V_\mathrm{Ed}\cdot(cot\theta+cot\alpha)}{2}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 = -F_\mathrm{s,BB}\cdot z+V_\mathrm{Ed}\cdot\cfrac{z}{2}\cdot(cot\theta+cot\alpha)}
z... Hebelarm der inneren Kräfte VEd... Bemessungswert der einwirkenden Querkraft cot θ... Druckstrebenneigungswinkel cot α... Neigungswinkel der Bügelbewehrung
- Ermittlung von Fs am Fachwerk[1]
- Momentengleichgewicht um Drehpunkt 2
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 = -F_\mathrm{s,FW}\cdot z+V_\mathrm{Ed}\cdot z \cdot cot\theta}
- ↓
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{s,FW}=V_\mathrm{Ed}\cdot cot\theta}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0 = -F_\mathrm{s,FW}\cdot z+V_\mathrm{Ed}\cdot z \cdot cot\theta}
z... Hebelarm der inneren Kräfte VEd... Bemessungswert der einwirkenden Querkraft cot θ... Druckstrebenneigungswinkel
Aufgrund der einleitend beschriebenen Unterschiede in den Berechnungsmodellen ergeben sich somit zwei unterschiedliche Bestimmungsgleichungen. Daraus lässt sich eine Gleichung zum Ermitteln der Differenzkraft ΔFs bestimmen:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_\mathrm{s}=F_\mathrm{s,FW}-F_\mathrm{s,BB}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_\mathrm{s}=V_\mathrm{Ed}\cdot cot\theta-\cfrac{V_\mathrm{Ed}\cdot(cot\theta+cot\alpha)}{2}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_\mathrm{s}=V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot\theta+cot\alpha)}
Die Größe der Differenzkraft ist sowohl abhängig von der im jeweiligen Betrachtungsschnitt einwirkenden Querkraft, als auch vom Druckstrebenneigungswinkel θ und dem Neigungswinkel der Querkraftbewehrung α. Dies gilt unabhängig des Beispiels auch für andere Tragsysteme und Belastungsarten.[1]
Veranschaulichung am Zugkraftdiagramm
Die Differenzkraft und das damit in Verbindung stehende Versatzmaß lassen sich weiterführend zur vorherigen Betrachtung über die Zugkraftlinien der Berechnungsmodelle veranschaulichen.
Nachfolgend wird das Zugkraftdiagramm zum Herleiten des Versatzmaßes Schrittweise ergänzt.
Fs-Linie aus Biegeberechnung
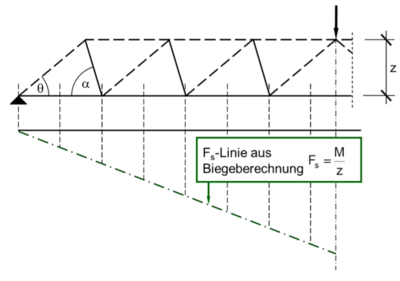
Beim Berechnungsmodell Biegebalken verläuft die Zugkraftlinie synchron zur Momentenlinie aus der Biegebemessung. Dies ist auf die Verbundwirkung zwischen Stahl und Beton zurückzuführen. Hierbei werden ständig Kräfte zwischen den beiden Werkstoffen ausgetauscht und es kommt somit zu einer gleichmäßig an den Momentenverlauf angepassten Zugkraft.
Die Zugkraft lässt sich über das am entsprechenden Betrachtungsschnitt einwirkende Biegemoment und den Hebelarm der inneren Kräfte bestimmen. Daraus lässt sich die Zugkraftlinie für das Berechnungsmodell Biegebalken Konstruieren. [1]
Fs-Linie für Einfach Fachwerk
Am Fachwerkmodell sind die Stabkräfte in den jeweiligen Bereichen der Untergurtebene jeweils konstant. Der Verlauf der Zugkraftlinie gestaltet sich somit entsprechend der Fachwerkfelder stufenförmig.
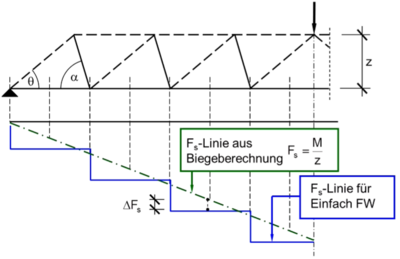
Projiziert man die Mittellinie eines Fachwerkfeldes abwärts auf die beiden Zugkraftlinien, lässt sich vertikal gemessen, eine Differenz feststellen. Hierbei handelt es sich um die zuvor abgeleitete Differenzkraft ΔFs.
- Notwendige Berücksichtigung:
- Der stufenförmige Zugkraftverlauf bildet lediglich ein virtuelles Einfach-Fachwerk ab. Real betrachtet liegen eine Vielzahl von Fachwerken aneinandergereiht und schrittweise versetzt im Bauteil. Hierbei spricht man dann von einem sogenannten Netzfachwerk. Dabei teilen sich die Kräfte gleichmäßig auf die untereinander versetzten Fachwerke auf.
- Somit sind weiterführend Betrachtungen am Netzfachwerk erforderlich.[1]
Fs-Linie für Netzfachwerk
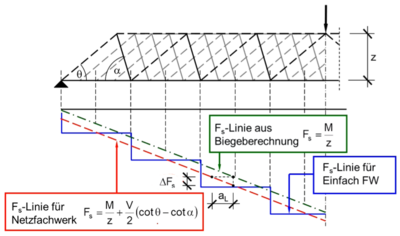
Erhöht man schrittweise die Anzahl der im Netzfachwerk befindlichen virtuellen Fachwerke, so werden die Abstufungen in der Zugkraftlinie dementsprechend immer kleiner. Mit der Annahme einer unendlich hohen Anzahl von Fachwerken wandelt sich der stufenförmige Verlauf schlussendlich zu einer kontinuierlichen Linie, welche parallel zur Zugkraftlinie aus der Biegebemessung verläuft. Die entstandene Linie entspricht dem Verlauf der tatsächlich auf die Bewehrung einwirkenden Zugkraft. Das vertikale Maß der Parallelverschiebung entspricht wie beim Einfach Fachwerk der Differenzkraft ΔFs.[1]
Die Größe der Zuggurtkraft am jeweiligen Betrachtungsschnitt ergibt sich somit zu:[1]
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_\mathrm{s} = \cfrac{M_\mathrm{Ed}}{z}+V_\mathrm{Ed}\cdot\cfrac{1}{2}\cdot(cot \theta-cot \alpha)}
VEd... Bemessungswert der einwirkenden Querkraft cot θ... Druckstrebenneigungswinkel cot α... Neigungswinkel der Bügelbewehrung z... Hebelarm der inneren Kräfte MEd... Bemessungswert des einwirkenden Momentes (Wert aus Momentengrenzlinie)
Gleichermaßen lässt sich die Zugkraftlinie horizontal Parallelverschieben. Das Maß der horizontalen Verschiebung entspricht dem Versatzmaß al.
Varianten zur Berücksichtigung der Zuggurtkraftdifferenz bei der Zugkraftdeckung
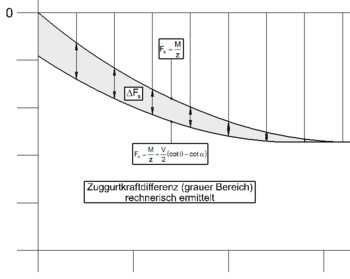
Variante 1 - Rechnerisches Ermitteln
Entsprechend des Querkraft- und Momentenverlaufes kann die Differenzkraft ΔFs rechnerisch ermittelt werden. Hierfür muss nicht nur die Momentengrenzlinie, sondern auch der vollständige Querkraftverlauf bekannt sein.
Weitere Details (siehe Zukkraftdeckung XXX)
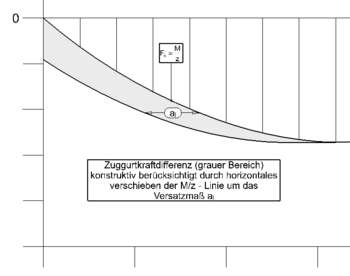
Variante 2 - Konstruktive Berücksichtigung über das Versatzmaß al
Hierbei wird die M/z – Linie horizontal um das Versatzmaß al (sieheXXX) parallelverschoben. Die Zuggurtkraftdifferenz ergibt sich somit automatisch über die Geometrie. Bei Bauteilen ohne Querkraftbewehrung ist dies generell die einzige Variante.
Weitere Details (siehe Zukkraftdeckung XXX)