Querkraftbemessung - Einwirkung: Unterschied zwischen den Versionen
| (24 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 15: | Zeile 15: | ||
==Direkte Lagerung== | ==Direkte Lagerung== | ||
| + | [[File:04_Querkraftabminderung.png|right|thumb|400px|Kraftfluss in direkt gelagerten Trägern unter Flächenlasten und auflagernahen Einzellasten (vgl. Reineck 2005)]] | ||
===Gleichstreckenlast=== | ===Gleichstreckenlast=== | ||
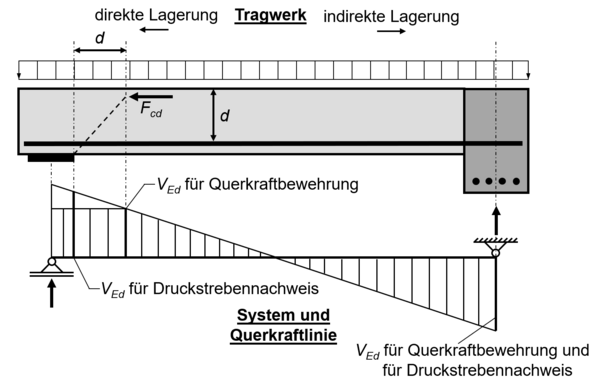
Bei der Belastung eines Feldes mit einer Gleichstreckenlast und direkter Lagerung bildet sich durch die Konzentration der Druckspannungen am Auflager ein fächerförmiges Spannungsfeld aus (siehe Abb.). Ein Teil der Flächenlast wird dadurch direkt in das Auflager geleitet und muss deshalb bei der Bemessung der Querkrafttragfähigkeit <math>V_\mathrm{Rd,c}</math> / <math>V_\mathrm{Rd,s}</math> nicht berücksichtigt werden. Die Lastanteile müssen jedoch trotzdem bei der Bemessung der Druckstrebentragfestigkeit <math>V_\mathrm{Rd,\max}</math> angesetzt werden, da das Druckfeld bis zum Auflagerrand belastet wird. <br> | Bei der Belastung eines Feldes mit einer Gleichstreckenlast und direkter Lagerung bildet sich durch die Konzentration der Druckspannungen am Auflager ein fächerförmiges Spannungsfeld aus (siehe Abb.). Ein Teil der Flächenlast wird dadurch direkt in das Auflager geleitet und muss deshalb bei der Bemessung der Querkrafttragfähigkeit <math>V_\mathrm{Rd,c}</math> / <math>V_\mathrm{Rd,s}</math> nicht berücksichtigt werden. Die Lastanteile müssen jedoch trotzdem bei der Bemessung der Druckstrebentragfestigkeit <math>V_\mathrm{Rd,\max}</math> angesetzt werden, da das Druckfeld bis zum Auflagerrand belastet wird. <br> | ||
| − | Gemäß Norm wird der maßgebende Querschnitt im Abstand | + | Gemäß Norm wird der maßgebende Querschnitt im Abstand <math>d</math> vom Auflagerrand festgelegt. Diese Annahme dient der Vereinfachung und befindet sich auf der sicheren Seite. Die tatsächliche Abgrenzung des fächerförmigen Druckfeldes liegt im Abstand <math> (z + d_\mathrm{1}) \cdot \cot \theta </math> vor der Auflagerkante. <ref name="Zilch" /> <ref name="Lohmeyer">BAAR, STEFAN und EBELING, KARSTEN: Lohmeyer Stahlbetonbau Bemessung - Konstruktion – Ausführung, Springer Vieweg Wiesbaden, 2016</ref> <ref name="EC2">FINGERLOOS, FRANK; HEEGER, JOSEF und ZILCH, KONRAD: Eurocode 2 für Deutschland - Kommentierte Fassung, Beuth Verlag GmbH, 2016</ref> |
| + | |||
===Einzellast=== | ===Einzellast=== | ||
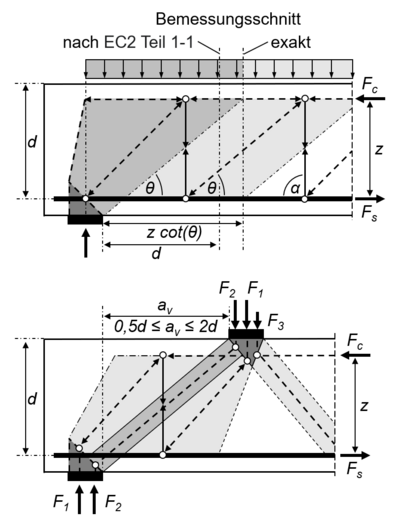
| + | Die einwirkende Querkraft aus auflagernahen Einzellasten muss nach einem alternativen Modell berechnet werden. Hierbei bildet sich ein Sprengwerk aus (siehe Abb.), das einen Anteil der Last (<math>F_\mathrm{2}</math>) direkt in das Auflager leitet. Versuche haben gezeigt, dass ein weiterer Anteil (<math>F_\mathrm{1}</math>) dennoch über die üblichen Querkrafttragmechanismen übertragen wird. Je näher sich die Einzellast am Auflagerrand befindet, desto größer ist der Anteil, der unmittelbar in das Auflager abgetragen wird. Allerdings ist die direkte Einleitung von Lastanteilen in das Auflager nur innerhalb der in der Norm (EC2 Teil 1-1) festgelegten Grenzwerte zulässig. So muss sich die Einzellast im Abstand <math>0,5d \leq a_\mathrm{v} \leq 2d</math> vom Rand des Auflagers befinden, das Bauteil von oben belastet werden und die Längsbewehrung vollständig am Auflager verankert sein, damit die einwirkende Querkraft mit dem Faktor <math> \beta </math> abgemindert werden darf. Bei <math>a_\mathrm{v} \leq 0,5d</math> ist der Wert <math>a_\mathrm{v} = 0,5d</math> anzusetzen. Für die Berechnung der Druckstrebentragfähigkeit <math>V_\mathrm{Rd,\max}</math> ist die Abminderung nicht zulässig. <ref name="Zilch" /> <ref name="EC2" /> <br> | ||
| + | |||
| + | <br> | ||
| + | :<math>\begin{align} \ \beta = \frac{a_\mathrm{v}}{2 \cdot d} \end{align}</math> | ||
| + | <br> | ||
| + | |||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | β ... || Abminderungsfaktor der einwirkenden Querkraft bei auflagernahen Einzellasten | ||
| + | |- | ||
| + | | a<sub>v</sub> ... || Abstand zwischen dem Auflagerrand und der einwirkenden Einzellast | ||
| + | |- | ||
| + | | d ... || statische Nutzhöhe | ||
| + | |} | ||
| + | <br /> | ||
==Indirekte Lagerung== | ==Indirekte Lagerung== | ||
| + | [[File:05_Querkraft_indirekt.png|right|thumb|400px|Spannungsfelder bei indirekter Lagerung]] | ||
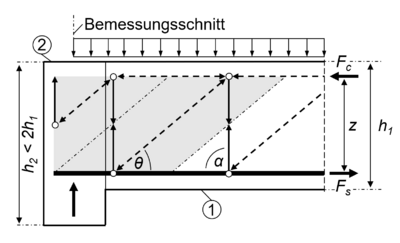
| + | Bei einer indirekten Lagerung entstehen – im Gegensatz zur direkten Lasteinleitung – keine konzentrierten Druckspannungen. Ein typisches Beispiel ist ein Bauteil (im Bild: Träger 1), das seitlich in einen Unterzug (im Bild: Träger 2) eingebunden ist. Die Druckspannungsfelder verlaufen dabei parallel – und nicht fächerförmig (vgl. „Direkte Auflagerung“) – in das Auflager, wodurch die günstig wirkenden Druckspannungen entfallen. Daraus ergibt sich, dass der Bemessungswert der Querkraft <math>V_\mathrm{Ed}</math> an der rechnerischen Auflagerlinie zu bestimmen ist. Die indirekt eingeleitete Auflagerkraft des lastbringenden Bauteils (Träger 1) muss über eine Aufhängebewehrung in die Druckzone des lastabtragenden Bauteils (Träger 2) hochgehängt und zusätzlich zur Querkraftbewehrung des Hauptträgers (Träger 2) angesetzt werden. Ein Unterzug kann jedoch auch als direkte Auflagerung gewertet werden, wenn die Höhe des stützenden Bauteils mehr als doppelt so groß ist wie die Höhe des zu stützenden Bauteils. <ref name="Zilch" /> <ref name="Baum">BAUMGART, RUDOLF: Bemessung für Querkraft, Massivbau, Hochschule Darmstadt, Skript, 2020</ref> | ||
| + | |||
| + | <br> | ||
| + | :<math>\begin{align} \ h_\mathrm{2} \geq 2 \cdot h_\mathrm{1} \end{align}</math> → direkte Lagerung | ||
| + | :<math>\begin{align} \ h_\mathrm{2} < 2 \cdot h_\mathrm{1} \end{align}</math> → indirekte Lagerung | ||
| + | <br> | ||
| + | |||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | h<sub>1</sub> ... || Höhe gestütztes Bauteil | ||
| + | |- | ||
| + | | h<sub>2</sub> ... || Höhe stützendes Bauteil | ||
| + | |} | ||
| + | <br> | ||
| + | |||
| + | =Einfluss von Vouten und geneigten Druckgurten= | ||
| + | [[File:06_geneigter Träger.png|right|thumb|400px|Kraftverlauf in einem Träger mit geneigtem Druck- und Zuggurt]] | ||
| + | [[File:07_geneigter_Träger_Faustregel.png|right|thumb|400px|Auswirkungen der Gurtneigungen auf die einwirkende Querkraft V<sub>Ed</sub>]] | ||
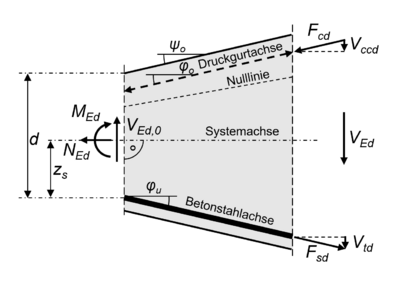
| + | Bei Trägern mit geneigten Gurten weisen sowohl die Druckspannungsresultierende <math>F_\mathrm{cd}</math> als auch die Betonstahlzugkraft <math>F_\mathrm{sd}</math> Querkraftanteile auf, die die Bemessungsquerkraft günstig oder ungünstig beeinflussen können. Die maßgebende einwirkende Querkraft sowie die Komponenten der geneigten Gurtkräfte ergeben sich aus den folgenden Formeln: <ref name="Zilch" /> <br> | ||
| + | |||
| + | <br> | ||
| + | :<math>\begin{align} \ V_\mathrm{Ed} = V_\mathrm{Ed,0} - V_\mathrm{ccd} - V_\mathrm{td} \end{align}</math> | ||
| + | <br> | ||
| + | :<math>\begin{align} \ V_\mathrm{ccd} = \frac{M_\mathrm{Eds}}{d} \cdot \tan\psi_\mathrm{o} \end{align}</math> | ||
| + | <br> | ||
| + | :<math>\begin{align} \ V_\mathrm{td} = \left( \frac{M_\mathrm{Eds}}{d} + N_\mathrm{Ed} \right) \cdot \tan\varphi_\mathrm{u} \end{align}</math> | ||
| + | <br> | ||
| + | :<math>\begin{align} \ M_\mathrm{Eds} = M_\mathrm{Ed} - N_\mathrm{Ed} \cdot z_\mathrm{s} \end{align}</math> | ||
| + | <br> | ||
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | V<sub>Ed</sub> ... || Bemessungswert der einwirkenden Querkraft | ||
| + | |- | ||
| + | | V<sub>Ed,0</sub> ... || Grundbemessungswert der einwirkenden Querkraft | ||
| + | |- | ||
| + | | V<sub>ccd</sub> ... || Querkraftkomponente aus der Druckspannungsresultierenden F<sub>cd</sub> | ||
| + | |- | ||
| + | | V<sub>td</sub> ... || Querkraftkomponente aus der Betonstahlzugkraft F<sub>sd</sub> | ||
| + | |- | ||
| + | | M<sub>Eds</sub> ... || das einwirkende Moment bezogen auf die Lage der Zugbewehrung | ||
| + | |- | ||
| + | | d ... || statische Nutzhöhe | ||
| + | |- | ||
| + | | ψ<sub>o</sub> ... || Neigung der Bauteiloberkante (≈φ<sub>o</sub>) | ||
| + | |- | ||
| + | | φ<sub>u</sub> ... || Neigung der Betonstahlachse | ||
| + | |- | ||
| + | | N<sub>Ed</sub> ... || Bemessungswert der Normalkraft | ||
| + | |- | ||
| + | | z<sub>s</sub> ... || Abstand Schwerelinie zu Biegezugbewehrung | ||
| + | |} | ||
| + | <br /> | ||
| + | Um die Formeln zu vereinfachen, kann näherungsweise davon ausgegangen werden, dass die Neigung des Druckgurts <math>\varphi_\mathrm{o}</math> identisch mit der Neigung der Bauteiloberkante ist. Zudem kann – auf der sicheren Seite liegend – anstelle des Hebelarms <math>z</math> | ||
| + | (Hebelarm der inneren Kräfte zwischen <math>F_\mathrm{cd}</math> und <math>F_\mathrm{sd}</math>) mit <math>d</math> gerechnet werden. Ist im Querschnitt eine Druckbewehrung vorhanden, kann deren Querkraftkomponente analog zu <math>V_\mathrm{ccd}</math> ermittelt werden. <ref name="Zilch" /> <ref name="Schneider"> ALBERT, ANDREJ: Schneider - Bautabellen für Ingenieure, 24. Auflage, Reguvis, 2020 </ref> | ||
| + | <br><br> | ||
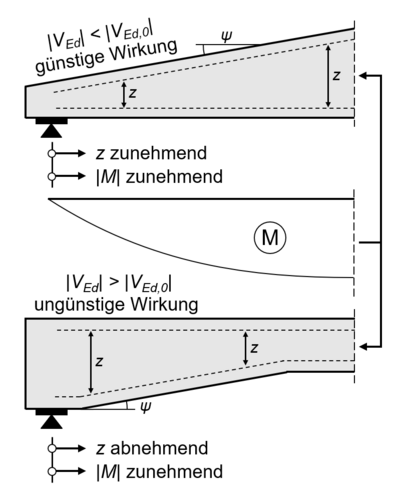
| + | Da die Querkraft direkt mit dem Verlauf der Momentenlinie über <math>V = dM / dx</math> verknüpft ist, lässt sich anhand der folgenden Faustregel schnell erkennen, ob ein geneigter Gurt den Querschnitt entlastet oder zusätzlich belastet: <br> | ||
| + | Nimmt der Betrag des Moments <math> \mid M \mid </math> und der Hebelarm der inneren Kräfte <math>z</math> gleichsinnig zu, wirken die zusätzlich entstehenden Querkraftkomponenten entlastend (günstig). Entwickeln sich <math> \mid M \mid </math> und <math>z</math> hingegen gegenläufig – das heißt, einer wird größer, der andere kleiner –, so wird das Bauteil zusätzlich belastet und der geneigte Gurt wirkt ungünstig. <ref name="Zilch" /> | ||
| + | <br /> | ||
=Quellen= | =Quellen= | ||
| Zeile 30: | Zeile 109: | ||
{{Seiteninfo | {{Seiteninfo | ||
| − | |Quality-flag = [[File:quality-flag- | + | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] |
| − | |Status = Seite | + | |Status = Seite fertig, ungeprüft| |
}} | }} | ||
[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
Aktuelle Version vom 18. Mai 2025, 17:40 Uhr
Für die Bemessung der Querkraft ist zunächst die Bestimmung der maßgeblichen Schnittgrößen entlang der Längsachse des Bauteils erforderlich. Der Querkraftverlauf weist nach den Regeln der Statik an den Auflagern und den Einleitungspunkten von Einzellasten sprunghafte Änderungen auf. An diesen Punkten treten typischerweise die Extremwerte auf. Da die Modelle zur Querkraftberechnung für B-Bereiche (lineare Spannungsverteilung, Bernoulli-Hypothese) entwickelt wurden, die maßgebenden Schnitte jedoch in D-Bereichen (nichtlineare Spannungsverteilung, unregelmäßige Bereiche) liegen, müssen bei der Nachweisführung in D-Bereichen bestimmte Besonderheiten berücksichtigt werden. Zudem kann durch die Idealisierung des Tragwerks die Ausbreitung der durch Lagerreaktionen oder Einzellasten hervorgerufenen Spannungen nicht abgebildet werden. [1]
Unterscheidung direkte und indirekte Lagerung
Zur Bestimmung der Bemessungsgrößen ist grundsätzlich zwischen zwei unterschiedlichen Arten der Auflagerung zu differenzieren:
- Direkte Lagerung
Die Auflagerkraft wird über Druckbeanspruchungen senkrecht zur Stabachse am Bauteilrand eingetragen.[1]
- Indirekte Lagerung
Die Einleitung der Auflagerkraft erfolgt über Zugkräfte bzw. verteilt über die Höhe des Trägers.[1]
Direkte Lagerung
Gleichstreckenlast
Bei der Belastung eines Feldes mit einer Gleichstreckenlast und direkter Lagerung bildet sich durch die Konzentration der Druckspannungen am Auflager ein fächerförmiges Spannungsfeld aus (siehe Abb.). Ein Teil der Flächenlast wird dadurch direkt in das Auflager geleitet und muss deshalb bei der Bemessung der Querkrafttragfähigkeit / nicht berücksichtigt werden. Die Lastanteile müssen jedoch trotzdem bei der Bemessung der Druckstrebentragfestigkeit angesetzt werden, da das Druckfeld bis zum Auflagerrand belastet wird.
Gemäß Norm wird der maßgebende Querschnitt im Abstand vom Auflagerrand festgelegt. Diese Annahme dient der Vereinfachung und befindet sich auf der sicheren Seite. Die tatsächliche Abgrenzung des fächerförmigen Druckfeldes liegt im Abstand vor der Auflagerkante. [1] [2] [3]
Einzellast
Die einwirkende Querkraft aus auflagernahen Einzellasten muss nach einem alternativen Modell berechnet werden. Hierbei bildet sich ein Sprengwerk aus (siehe Abb.), das einen Anteil der Last () direkt in das Auflager leitet. Versuche haben gezeigt, dass ein weiterer Anteil () dennoch über die üblichen Querkrafttragmechanismen übertragen wird. Je näher sich die Einzellast am Auflagerrand befindet, desto größer ist der Anteil, der unmittelbar in das Auflager abgetragen wird. Allerdings ist die direkte Einleitung von Lastanteilen in das Auflager nur innerhalb der in der Norm (EC2 Teil 1-1) festgelegten Grenzwerte zulässig. So muss sich die Einzellast im Abstand vom Rand des Auflagers befinden, das Bauteil von oben belastet werden und die Längsbewehrung vollständig am Auflager verankert sein, damit die einwirkende Querkraft mit dem Faktor abgemindert werden darf. Bei ist der Wert anzusetzen. Für die Berechnung der Druckstrebentragfähigkeit ist die Abminderung nicht zulässig. [1] [3]
wobei:
β ... Abminderungsfaktor der einwirkenden Querkraft bei auflagernahen Einzellasten av ... Abstand zwischen dem Auflagerrand und der einwirkenden Einzellast d ... statische Nutzhöhe
Indirekte Lagerung
Bei einer indirekten Lagerung entstehen – im Gegensatz zur direkten Lasteinleitung – keine konzentrierten Druckspannungen. Ein typisches Beispiel ist ein Bauteil (im Bild: Träger 1), das seitlich in einen Unterzug (im Bild: Träger 2) eingebunden ist. Die Druckspannungsfelder verlaufen dabei parallel – und nicht fächerförmig (vgl. „Direkte Auflagerung“) – in das Auflager, wodurch die günstig wirkenden Druckspannungen entfallen. Daraus ergibt sich, dass der Bemessungswert der Querkraft an der rechnerischen Auflagerlinie zu bestimmen ist. Die indirekt eingeleitete Auflagerkraft des lastbringenden Bauteils (Träger 1) muss über eine Aufhängebewehrung in die Druckzone des lastabtragenden Bauteils (Träger 2) hochgehängt und zusätzlich zur Querkraftbewehrung des Hauptträgers (Träger 2) angesetzt werden. Ein Unterzug kann jedoch auch als direkte Auflagerung gewertet werden, wenn die Höhe des stützenden Bauteils mehr als doppelt so groß ist wie die Höhe des zu stützenden Bauteils. [1] [4]
- → direkte Lagerung
- → indirekte Lagerung
wobei:
h1 ... Höhe gestütztes Bauteil h2 ... Höhe stützendes Bauteil
Einfluss von Vouten und geneigten Druckgurten
Bei Trägern mit geneigten Gurten weisen sowohl die Druckspannungsresultierende als auch die Betonstahlzugkraft Querkraftanteile auf, die die Bemessungsquerkraft günstig oder ungünstig beeinflussen können. Die maßgebende einwirkende Querkraft sowie die Komponenten der geneigten Gurtkräfte ergeben sich aus den folgenden Formeln: [1]
wobei:
VEd ... Bemessungswert der einwirkenden Querkraft VEd,0 ... Grundbemessungswert der einwirkenden Querkraft Vccd ... Querkraftkomponente aus der Druckspannungsresultierenden Fcd Vtd ... Querkraftkomponente aus der Betonstahlzugkraft Fsd MEds ... das einwirkende Moment bezogen auf die Lage der Zugbewehrung d ... statische Nutzhöhe ψo ... Neigung der Bauteiloberkante (≈φo) φu ... Neigung der Betonstahlachse NEd ... Bemessungswert der Normalkraft zs ... Abstand Schwerelinie zu Biegezugbewehrung
Um die Formeln zu vereinfachen, kann näherungsweise davon ausgegangen werden, dass die Neigung des Druckgurts identisch mit der Neigung der Bauteiloberkante ist. Zudem kann – auf der sicheren Seite liegend – anstelle des Hebelarms
(Hebelarm der inneren Kräfte zwischen und ) mit gerechnet werden. Ist im Querschnitt eine Druckbewehrung vorhanden, kann deren Querkraftkomponente analog zu ermittelt werden. [1] [5]
Da die Querkraft direkt mit dem Verlauf der Momentenlinie über verknüpft ist, lässt sich anhand der folgenden Faustregel schnell erkennen, ob ein geneigter Gurt den Querschnitt entlastet oder zusätzlich belastet:
Nimmt der Betrag des Moments und der Hebelarm der inneren Kräfte gleichsinnig zu, wirken die zusätzlich entstehenden Querkraftkomponenten entlastend (günstig). Entwickeln sich und hingegen gegenläufig – das heißt, einer wird größer, der andere kleiner –, so wird das Bauteil zusätzlich belastet und der geneigte Gurt wirkt ungünstig. [1]
Quellen
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 ZILCH, KONRAD und ZEHETMAIER, GERHARD: Bemessung im konstruktiven Betonbau, Springer-Verlag Berlin Heidelberg, 2010
- ↑ BAAR, STEFAN und EBELING, KARSTEN: Lohmeyer Stahlbetonbau Bemessung - Konstruktion – Ausführung, Springer Vieweg Wiesbaden, 2016
- ↑ 3,0 3,1 FINGERLOOS, FRANK; HEEGER, JOSEF und ZILCH, KONRAD: Eurocode 2 für Deutschland - Kommentierte Fassung, Beuth Verlag GmbH, 2016
- ↑ BAUMGART, RUDOLF: Bemessung für Querkraft, Massivbau, Hochschule Darmstadt, Skript, 2020
- ↑ ALBERT, ANDREJ: Schneider - Bautabellen für Ingenieure, 24. Auflage, Reguvis, 2020
Seiteninfo
|