Wandartiger Träger

Definition

Wandartige Träger sind ebene Flächentragwerke, die in Richtung Ihrer Mittelebene belastet werden. Sie werden überwiegend auf Biegung beansprucht, der Lastabtrag erfolgt in vertikaler Richtung. Im Gegensatz zu einem "Balken" ist das Verhältnis der Bauteilhöhe h zur Stützweite l viel größer.

Einfeldträger

• ${\cfrac {h}{l}}\leq 0,5~~~~~~~~~{(Balken)}$
  

• ${\cfrac {h}{l}}>0,5~~~~~~~~~{(Wandartiger~Traeger)}$
  

Zweifeldträger und Endfelder von Durchlaufträger

• ${\cfrac {h}{l}}>0,4~~~~~~~~~{(Wandartiger~Traeger)}$
  

Innenfelder von Durchlaufträger

• ${\cfrac {h}{l}}>0,3~~~~~~~~~{(Wandartiger~Traeger)}$
  

Theoretischer Hintergrund

Spannungsverteilung

Längsspannungen

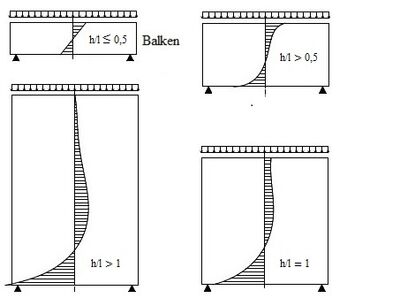
Aufgrund der im Verhältnis zur Höhe kurzen Spannweite, kann bei wandartigen Trägern nicht mehr vom Ebenbleiben des Querschnitts ausgegangen werden. Die Längsspannungen verlaufen nicht mehr linear über die Querschnittshöhe, sondern krummlinig. Je gedrungener die Scheibe, desto größer werden die Abweichungen der Längsspannungen zum geradlinigen Spannungsverlauf nach Navier.(siehe Abb.2.1.1.1)

• Abb. 2.1.1.1 Verlauf der Längsspannungen eines einfeldrigen wandartigen Trägers

Dabei ist zu erkennen, dass ab einem Verhältnis von l/h = 1 kaum noch Biegedruckspannungen im oberen Bereich vorhanden sind

Hinweis:

• Der Verlauf der Längsspannungen bleibt unbeeinflusst davon, ob die Last am oberen oder unteren Rand des wandartigen Trägers angreift. Anders hingegen ist es bei den Querspannungen.

Querspannungen

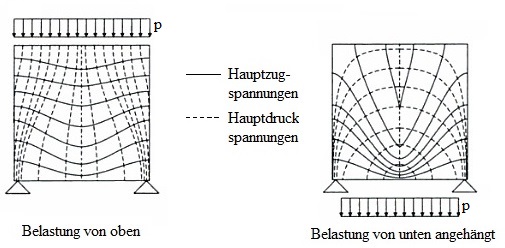
Anhand von Hauptspannungstrajektorien lässt sich der Verlauf der Querspannungen sehr gut verdeutlichen.
In den Abbildungen 2.1.2.1 und 2.1.2.2 wird der Verlauf der Querspannungen und der Hauptspannungstrajektorien dargestellt. Je nach Belastung ergeben sich unterschiedliche Verläufe. Wie in Abschnitt 2.1.1 erwähnt, bleiben die Längsspannungen ubeeinflusst davon, ob die Last am oberen oder am unteren Rand angreift.

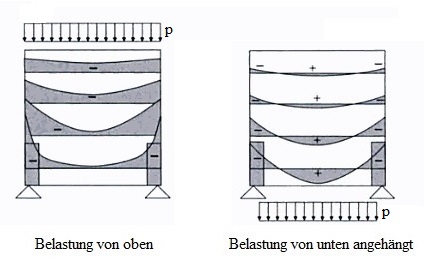
• Abb. 2.1.2.1 Verlauf der Querspannungen eines einfeldrigen wandartigen Trägers

• Abb.2.1.2.2 Verlauf der Hauptspannungstrajektorien eines einfeldrigen wandartigen Trägers
  

Anhand der Hauptspannungstrajektorien wird bei diesem Beispiel deutlich, dass die Druckspannungen sowohl bei der Belastung von oben als auch von unten im Auflagerbereich am größten sind.
Im Fall der von oben belasteten Wand verlaufen die Zugtrajektorien im gesamten Wandbereich sehr flach. Die Zugspannungen sind im Feldbereich etwa genauso groß, wie im Bereich des Auflagers. Für die Bewehrungsführung bedeutet das, dass die Bewehrung ungestaffelt von Auflager zu Auflager zuführen ist. Sie wird im unteren Bereich angeordnet und bildet ein Zugband aus.
Bei der Belastung von unten ist es im unteren Bereich der Wand ähnlich. Hinzu kommt, dass die Zugtrajektorien im oberen Bereich fast vertikal durch die Wand verlaufen. Diese Zugspannungen sind durch eine Aufhängebewehrung aufzunehmen.

Quellen

Seiteninfo Status: in Bearbeitung Modul-Version: 2015.026