Durchstanzen

Allgemeines zum Durchstanzen

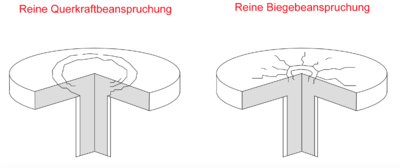
Wird eine konzentrierte Last auf eine verhältnismäßig kleine Einleitungsfläche eines Plattentragwerks (z.B. Deckenplatte oder Fundament) aufgebracht, so kommt es zu einem örtlichen Querkraftversagen .
Dies äußert sich bei relativ geringen Lasten durch auftretende Biegerisse in radialer Richtung. Wird die Last erhöht, so kommt es als Folge dessen zum Reißen des Betons in tangentialer Richtung (Querkraftrisse).
Durch die Vereinigung zu Durchstanzrissen verursachen diese einen Bruch .
Trennt sich der betroffenen Plattenbereich heraus, so entsteht der typische kegel- oder pyramidenförmige Körper. Diese Art des Versagens geschieht ohne eine ausgeprägte Vorankündigung. Es kommt zu einem fortschreitenden Kollaps der vollständigen Konstruktion .
Folglich ist diese Art von Nachweis das maßgebende Kriterium bei der Bemessung einer Deckenplatte. Da das Durchstanzversagen ein Sonderfall der Querkraftbeanspruchung darstellt, besteht ein Zusammenhang zwischen beiden Bemessungsansätzen .

Obwohl die Durchstanztragfähigkeit und das Biegetragverhalten sich gegenseitig beeinflussen (siehe Bild 1), sind ihre Berechnung separat durchzuführen. .

Bild 1: Rissbilder bei reiner Querkraft- und reiner Biegebeanspruchung

Die Durchstanztragfähigkeit wird durch Bauteileigenschaften wie

• der Betonfestigkeit,
• den Querschnittabmessungen,
• der Bewehrungsmenge in der Zugzone,
• eine durch Vorspannung entstehende Normaldruckkraft und
• die vorgesehene Durchstanzbewehrung maßgebend beeinflusst .

Bei der Nachweisführung müssen folgende Versagen verursachende Komponenten einbezogen werden :

• eine Überschreitung der Betonzugfestigkeit,
• ein Versagen der Betondruckzone,
• ein örtliches Verbundversagen der Biegezugbewehrung
• und eine unzureichende Verankerung der Durchstanzbewehrung

Der zu führende Nachweis besagt, dass die auf den kritischen Rundschnitt $d\cdot u$ bezogene einwirkende Querkraft $\nu _{Ed}$ geringer ausfällt, als der Bemessungswiderstand $\nu _{Rd}$.
Der Nachweis lautet wie folgt:

$\nu _{Ed}=\beta \cdot {\frac {V_{Ed}}{u_{i}\cdot d}}\leq \nu _{Rd}$

Es findet hierbei eine Unterscheidung in Bauteilen mit und ohne Durchstanzbewehrung statt.

Bauteile ohne Durchstanzbewehrung

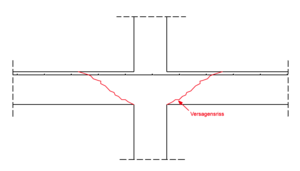
Bild 2: Versagensmechanismus bei einem Bauteil ohne Durchstanzbewehrung

Bei Plattentragwerken ohne Durchstanzbewehrung (siehe Bild 2) muss der folgende Nachweis klären, ob die Tragfähigkeit des Betons im kritischen Rundschnitt ausreichend ist und die auftretende Querkraft den Bauteilwiderstand somit nicht überschreitet .

Im Allgemeinen gilt:

$\nu _{Ed}\leq \nu _{Rd}$

Somit muss bei Bauteilen ohne Durchstanzbewehrung die Querkrafttragfähigkeit des Betons im kritischen Rundschnitt größer sein, als die vorherrschende Einwirkung:

$\nu _{Ed}\leq \nu _{Rd,c}$

Ist der Bemessungswiderstand $\nu _{Ed}$ größer als der Bemessungswert der Querkraft $\nu _{Rd}$ , so ist eine Durchstanzbewehrung vorzusehen, welche beispielsweise durch Bügel gebildet werden kann.
Ist diese Maßnahme nicht ausreichend, können tragfähigkeitserhöhende Einbauteile vorgesehen werden.


Genauere Informationen zum Nachweis für Bauteile ohne Durchstanzbewehrung : Punktförmig gestützte Platten und Fundamente ohne Durchstanzbewehrung

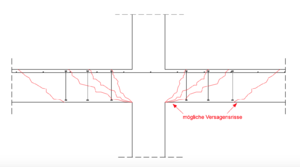
Bauteile mit Durchstanzbewehrung

Wird Durchstanzbewehrung benötigt, so muss auf mehreren Rundschnitten u_i weitere Querkraftnachweise geführt werden.

Bild 3: Versagensmechanismus bei Bauteilen mit Durchstanzbewehrung

Des Weiteren kann zur Steigerung der Tragfähigkeit zusätzlich zur Durchstanzbewehrung eine Querkraftbewehrung in Form von aufgebogenen Stäben, Bügeln, S-Haken oder Dübelleisten in Betracht gezogen werden. Werden solche verwendet, ist eine zweite Reihe an Schubbewehrung anzuordnen, auch wenn diese rechnerisch nicht erforderlich ist. Bei der Ausführung von Durchstanzbewehrung müssen mehrere Versagensmechanismen (siehe Bild 3) betrachtet werden :

Betonversagen: die maximale Schubspannung $\nu _{Rd,Ed}$ darf nicht größer ausfallen, als der Bemessungswert des maximalen Durchstanzwiderstands $\nu _{Rd,max}$.

$\nu _{Ed}\leq \nu _{Rd,max}$

Stahlversagen: die Tragfähigkeit des Querschnitts mit Durchstanzbewehrung muss in jedem Rundschnitt gewährleistet sein.

$\nu _{Ed}\leq \nu _{Rd,cs}$

Die Querkrafttragfähigkeit muss in der Umgebung außerhalb des durchstanzbewehrtem Bereichs ohne Querkraftbewehrung gegeben sein.

$\nu _{Ed}\leq \nu _{Rd,c,out}$

Bemessungswert der Einwirkung

Die als Spannung angegebene Bemessungsquerkraft bezieht sich auf die Querschnittsfläche des kritischen Rundschnitts .
Die Gleichung dafür lautet:

$\nu _{Ed}=\beta \cdot {\frac {V_{Ed}}{u_{i}\cdot d}}$

Der benötigte Korrekturfaktor β berücksichtigt hierbei eine einseitig erhöhte Belastung.

Punktförmig gestützte Platten und Fundamente mit Durchstanzbewehrung

Ist der Bemessungswert der Einwirkung $\nu _{Ed}$ größer als der Widerstand $\nu _{Rd,c}$ so ist eine Durchstanzbewehrung auszuführen. Bei dem so entstandenen räumlichen Fachwerkmodell werden die Zugstreben von der Durchstanzbewehrung gebildet . Die möglichen Versagensmechanismen müssen durch mehrere Nachweise geprüft werden. Die Maximaltragfähigkeit $\nu _{Rd,max}$ wird benötigt, um die ausreichende Bewehrungsmenge zu ermitteln. Dieser Wert bezieht sich auf den kritischen Rundschnitt u₁ und sagt aus, ob die Einwirkung $\nu _{Ed}$ durch eine Durchstanzbewehrung aufgenommen werden kann .

$\nu _{Ed,u1}=\beta \cdot {\frac {V_{Ed}}{u_{1}\cdot d}}\leq \nu _{Rd,max}=1,4\cdot \nu _{Rd,c,u1}$(NA)

Bei der Berechnung von $\nu _{Rd,c}$ darf in diesem Fall keine Betondrucknormalspannung $\sigma _{cp}$ durch eine Vorspannung berücksichtig werden .

Bild 17: Querkraftdeckung bei Bügeln als Durchstanzbewehrung

Der Nachweis der Durchstanzbewehrung erfolgt ebenfalls für den kritischen Rundschnitt u₁. Die so ermittelte Bewehrung wird auf mehrere Rundschnitte verteilt:

$\nu _{Rd,cs}=0,75\cdot \nu _{Rd,c}+1,5\cdot {\frac {d}{s_{r}}}\cdot {\frac {A_{sw}\cdot f_{ywd,ef\cdot \sin(\alpha )}}{u_{1}\cdot d}}\geq \nu _{Ed,u_{1}}$(NA)

Hieraus ergibt sich die erforderliche Durchstanzbewehrung:

$A_{swJ}=\kappa _{swJ}\cdot {\frac {(\nu _{Ed}-0,75\cdot \nu _{Rd,c})\cdot d\cdot u_{1}}{1,5\cdot {\frac {d}{s_{r}}}\cdot f_{ywd,ef}}}$

mit
$f_{fwd,ef}=250+0,25\cdot d\leq f_{ywd}$ in N/mm^2
In den ersten zwei Reihen des Rundschnitts ist der Betonstahlquerschnitt $Asw$ aufgrund einer Unterschätzung mit dem Faktor$\kappa$ zu erhöhen.

• 1.Reihe $0,3d\leq s_{r1}\leq 0,5d$:
  

$\kappa _{sw,1}=2,5$

• 2.Reihe $s_{r2}\leq 0,75d$:
  

$\kappa _{sw,2}=1,4$

• bis zur letzten Reihe $(s_{ri}\leq 0,75d)$:
  

$\kappa _{sw,i}=1,0$

Es wird der größte Wert für s_r gewählt, jedoch nicht größer als $s_{r,max}=0,75d$
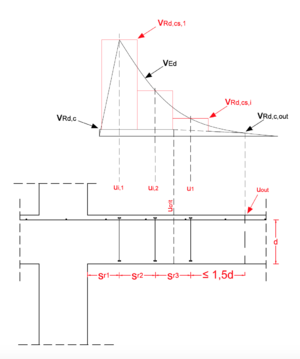
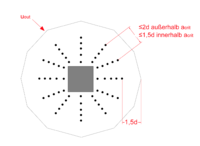
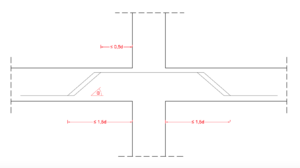
Es sind mindestens zwei Bewehrungsreihen zu verlegen, welche wie in Bild 16 anzulegen sind. Die letzte Bewehrungsreihe ist im Abstand $\leq 1,5d$vom äußeren Rundschnitt $u_{out}$ anzulegen (siehe Bild 17).

Äußerer Rundschnitt

Dieser ergibt sich wie folgt:

$u_{out}=\beta \cdot {\frac {V_{Ed}}{\nu _{Rd,c}\cdot d}}$

Somit muss nachgewiesen werden, dass im kritischen Rundschnitt u_out keine Durchstanzbewehrung mehr erforderlich ist:
$\nu _{Ed,out}=\beta \cdot {\frac {V_{Ed}}{\nu _{out}\cdot d}}\leq \nu _{Rd,c}$

Zur Bestimmung des Betontraganteils $\nu _{Rd,c}wirdderFaktor<math>C_{Rd,c}=0,15/\gamma _{c}$ angesetzt.
Dieser Wert stellt hier die Tragfähigkeit einer liniengelagerten Platte ohne Querkraftbewehrung unter Berücksichtigung des Längsbewehrungsgrads<math\rho_l</math> im äußeren Rundschnitt dar .

Besonderheiten von Fundamenten und Bodenplatten

Bei Fundamenten ist die reduzierte einwirkende Querkraft $V_{Ed,red}$ von den ersten zwei Bewehrungsreihen voll aufzunehmen, dabei ist der Betontraganteil nicht in Abzug zu bringen. Die erforderliche Bewehrung ist gleichmäßig auf die ersten beiden Reihen zu verteilen .

• 1. Reihe im Abstand $s_{0}=0,3d$ und
• 2. Reihe im Abstand $s_{0}+s_{1}=0,8d$

Die Maximaltragfähigkeit des Fundaments setzt sich folgendermaßen zusammen:

$\nu _{Rd,max}=1,4\cdot \nu _{Rd,c,u1}$

Bei Fundamenten ist u₁ gegebenenfalls durch den interativ ermittelten Wert von u im Abstand acrit zu ersetzen. Hier darf bei der Ermittlung von $\nu _{Rd,c}$ keine Betondruckspannung$\sigma _{cp}$ durch eine Vorspannung berücksichtigt werden . Wird der Maximalwert überschritten, so müssen Maßnahmen zur Steigerung des Querkraftwiderstands ergriffen werden.

Hierzu gehören:

• Erhöhung der Betongüte
• Vergrößerung der Fundamentenhöhe
• oder Erhöhung des Bewehrungsgrades

Folgende Nachweise sind zu führen :

• für Bügelbewehrung:

$\beta \cdot V_{Ed,red}\leq V_{Rd,s}=A_{sw,1+2}\cdot f_{ywd,ef}$

Umgestellt zur Ermittlung der Bewehrungsmenge:

$A_{sw,1+2}={\frac {\beta \cdot V_{Ed,red}}{f_{ywd,ef}}}$

• für Schrägbewehrung:

$\beta \cdot V_{Ed,red}\leq V_{Rd,s}=1,3\cdot A_{sw,1+2}\cdot f_{ywd,ef}\cdot \sin(\alpha )$

Weitere eventuell erforderliche Bewehrungsreihen werden mit 33 % von $A_{sw,1+2}$ versehen.

$0,33\cdot A_{sw,1+2}$

Hierbei darf innerhalb der betrachteten Bewehrungsreihe die Bodenpressung der Fundamentfläche in Abzug gebracht werden .

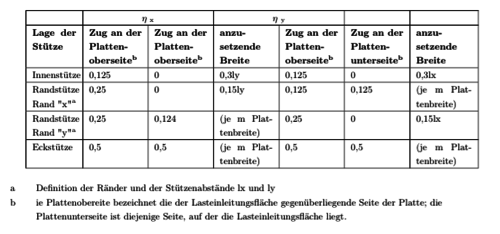
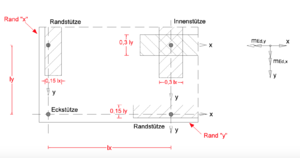
Mindestmomente für Platten-Stützen-Verbindungen

Bild 19: Momentenbeiwert und Verteilungsbreiten der Mindestmomente mEd

Bild 20: Ansatz der Mindestmomente

Die Sicherheit gegen Durchstanzen bei nicht berücksichtigten Exzentrizitäten wird durch die Berechnung der Mindestmomente $mEd,x$ und $mEd,y$ gewährleistet. Diese sollen eine Begrenzung der Schubrissweiten und die Erhaltung des räumlichen Tragmodells sicherstellen.
Bei Erhalt von größeren Werten durch die Schnittgrößenermittlung sind diese maßgebend . Es dürfen nur die Bewahrungsstäbe berücksichtigt werden, welche außerhalb des kritischen Rundschnitts verankert sind.

Die Mindestmomente ergeben sich wie folgt:

• $mEd,x=\eta _{x}\cdot V_{Ed}$
• $mEd,y=\eta _{y}\cdot V_{Ed}$

Die Anordnung der Bewehrung erfolg nach Bild 20.

Mindestbewehrung und Konstruktionsregeln

Bild 21: Schrägstäbe als Durchstanzbewehrung

Ist in einer Platte eine Durchstanzbewehrung vorzusehen, so muss die Platte eine Mindestdicke von 20 cm aufweisen . Die vorgesehene Durchstanzbewehrung ist bei Deckenplatten in der oberen, bei Fundamenten in der unteren Lage anzuordnen, da diese die Zugseiten darstellen. Bei der Ermittlung von Durchstanzbewehrung, darf die Grundbewehrung angerechnet werden. Existieren nebenliegende Durchbrüche, so dürfen diese nicht größer als 1/3 der Stützenbreite, beziehungsweise des Durchmessers der Stütze ausfallen . Der Stabdurchmesser der Durchstanzbewehrung ist an die mittlere Nutzhöhe der Platte anzupassen:

• bei Bügeln:

∅$\leq 0,05d$

• bei Schrägaufbiegung:

∅$\leq 0,08d$

Maximaler tangentialer Abstand der Bügelschenkel

• innerhalb des kritischen Rundschnitts s_t= 1,5d
• außerhalb des kritischen Rundschnitts s_t=2,0d

Als Mindestbewehrung gilt (je Bügelschenkel)(NA):

$A_{sw,min}=A_{s}\cdot \sin(\alpha )={\frac {0,08\cdot {\sqrt {f_{ck}}}\cdot s_{r}\cdot s_{t}}{f_{yk}\cdot 1,5}}$

Schrägstäbe sind in einem Winkel von $45<\alpha <60$ zur Bauteilachse auszuführen.

Dabei ist ihre Aufbiegungen im Bereich $\leq 1,5d$ um die Stütze anzulegen. Bei aufgebogenen Schrägstäben ist eine Bewehrungsreihe ausreichend, welche mit einem s_r= 0,67d angenommen werde kann . Bei der Berechnung des Bauteiltragwiderstands ist das Verhältnis d/s_r= 0,53 zu beachten. Des Weiteren kann die Bewehrung bis f_ywd,ef = f_ywd ausgereizt werden, da Schrägstäbe selbst bei dünnen Platten die Streckgrenze erreichen . Darüber hinaus müssen mindestens 50 % der Längsbewehrung in radialer oder tangentialer Richtung von der Durchstanzbewehrung umschlossen werden.
Querkraftzulagen sind als Durchstanzbewehrung unzulässig .

Quellen

Seiteninfo Status: in Bearbeitung Modul-Version: 2015.0240