Bemessung bei zweiachsiger Biegung und Längskraft (Bsp.): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| + | {{Lesernavigation 5 Links | ||
| + | |Link1 = [[Hauptseite]] | ||
| + | |Link2 = [[Stahlbetonbau]] | ||
| + | |Link3 = [[:Kategorie:Beispiele-Stahlbetonbau|Beispiele]] | ||
| + | |Link4 = [[:Kategorie:Hinweise für Leser|Hinweise für Leser]] | ||
| + | |Link5 = [[:Kategorie:Hinweise für Autoren|Hinweise für Autoren]] | ||
| + | }} | ||
| + | <br /> | ||
| + | |||
== Handrechnung == | == Handrechnung == | ||
Version vom 10. Dezember 2015, 17:47 Uhr
| Hauptseite • Stahlbetonbau • Beispiele • Hinweise für Leser • Hinweise für Autoren |
Handrechnung
Einwirkungen
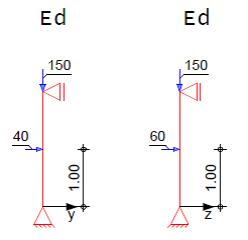
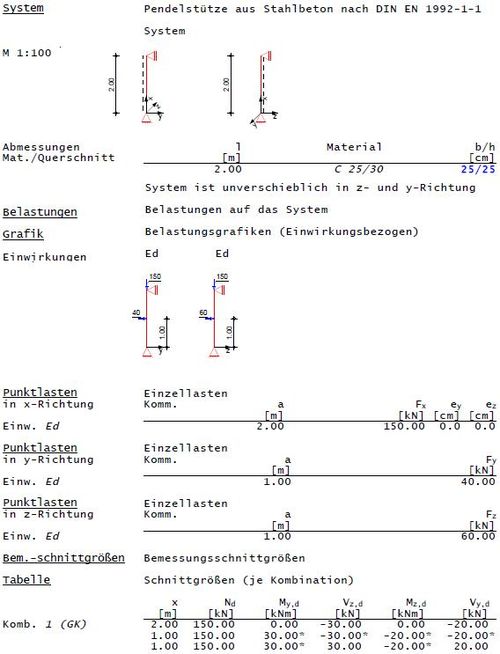
Querschnitts-, Systemabmessungen und Betongüte
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\begin{array}{l}b/h=25/25cm\\{{d}_{1}}=5,4cm\\C25/30\\l=2m\end{array}}}
Schnittgrößen (angreifende Horizontalkräfte in 1m Höhe)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{N}_{Ed}}=-150kN\\{{M}_{y,Ed}}={{H}_{z}}\cdot l\cdot \frac{1}{4}=60\cdot 2\cdot 0,25=30kNm\\{{M}_{z,Ed}}={{H}_{y}}\cdot l\cdot \frac{1}{4}=40\cdot 2\cdot 0,25=20kNm\end{array}}
Schlankheitskriterium
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{l}_{0}}=\beta \cdot {{l}_{col}}=1\cdot 2=2m\\\lambda =\frac{{{l}_{0}}}{i}=\frac{{{l}_{0}}}{\sqrt{\frac{I}{A}}}=\frac{200}{\sqrt{\frac{{{25}^{4}}/12}{{{25}^{2}}}}}=27,7\end{array}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{-150}{{{25}^{2}}\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,17}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{\lim }}=\frac{16}{\sqrt{n}}=\frac{16}{\sqrt{0,17}}=38,9}
Nachweis nach Theorie I. Ordnung legitimiert.
Bezogene Schnittgrößen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-150}{{{25}^{2}}\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,17\\{{\mu }_{y,Ed}}=\frac{{{M}_{y,Ed}}}{b\cdot h{}^\text{2}\cdot {{f}_{cd}}}=\frac{3000}{25{}^\text{3}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,14\\{{\mu }_{z,Ed}}=\frac{{{M}_{Ed}}}{b{}^\text{2}\cdot h\cdot {{f}_{cd}}}=\frac{2000}{25{}^\text{3}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,09\end{array}}
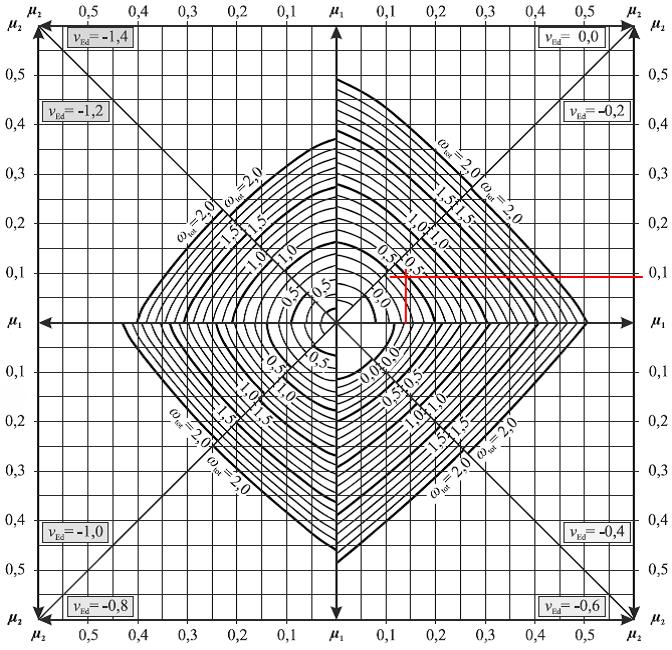
Bemessung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}\frac{{{d}_{1}}}{h}=\frac{{{b}_{1}}}{b}=\frac{0,054}{0,25}=0,22\approx 0,2\\\end{array}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\mu }_{1}}=\max \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}=\max \{0,14;0,09\}=0,14\\{{\mu }_{2}}=\min \{{{\mu }_{Ed,y}};{{\mu }_{Ed,z}}\}=\min \{0,14;0,09\}=0,09\end{array}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\omega }_{tot}}=0,5\\{{A}_{s,tot}}={{\omega }_{tot}}\cdot \frac{b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}=0,5\cdot \frac{25{}^\text{2}}{\frac{50}{1,15}/0,85\cdot \frac{2,5}{1,5}}=10,2cm{}^\text{2}\end{array}}
gewählt: 12ø12 über den Umfang verteilt, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s,vorh}}=13,57cm{}^\text{2}}
mb-Berechnung
Quellen
Seiteninfo
|