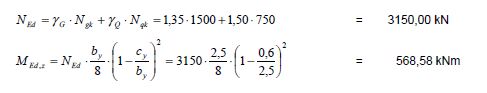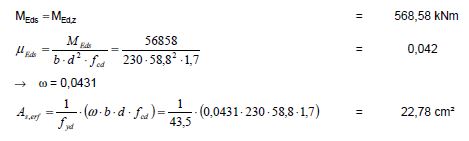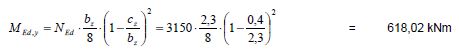Beispiel Fundamentberechnung für S510.de (Ermittlung der Längsbewehrung): Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Mwulf (Diskussion | Beiträge) |
Mwulf (Diskussion | Beiträge) |
||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
|Link1 = [[Stahlbetonbau]] | |Link1 = [[Stahlbetonbau]] | ||
|Link2 = [[:Kategorie:MB-AEC Baustatik-Module Stahlbetonbau|MB-AEC-Module Stahlbetonbau]] | |Link2 = [[:Kategorie:MB-AEC Baustatik-Module Stahlbetonbau|MB-AEC-Module Stahlbetonbau]] | ||
| − | |Link3 = [[ | + | |Link3 = [[Bemessung eines Einzelfundaments (Bsp.)]] |
}} | }} | ||
<br /> | <br /> | ||
| Zeile 55: | Zeile 55: | ||
==mb-Vergleichsrechnung== | ==mb-Vergleichsrechnung== | ||
| − | *''' | + | *'''Biegebemessung''' |
:Die Bemessungsmomente für die y- und z-Richtung (M<sub>z,d,max</sub> und M<sub>y,d,max</sub>) stimmen mit der Handrechnung überein. | :Die Bemessungsmomente für die y- und z-Richtung (M<sub>z,d,max</sub> und M<sub>y,d,max</sub>) stimmen mit der Handrechnung überein. | ||
:::M<sub>Ed,z</sub> = 568,58 kNm <math>\approx</math> 567,63 kNm = M<sub>z,d,max</sub> | :::M<sub>Ed,z</sub> = 568,58 kNm <math>\approx</math> 567,63 kNm = M<sub>z,d,max</sub> | ||
:::M<sub>Ed,y</sub> = 618,02 kNm <math>\approx</math> 616,99 kNm = M<sub>y,d,max</sub> | :::M<sub>Ed,y</sub> = 618,02 kNm <math>\approx</math> 616,99 kNm = M<sub>y,d,max</sub> | ||
[[Datei: Beispiel_Fundamentberechnung_inkl_Durchstanzen_(S510.de)_29.JPG|600px|tumb|rahmenlos|rand]] | [[Datei: Beispiel_Fundamentberechnung_inkl_Durchstanzen_(S510.de)_29.JPG|600px|tumb|rahmenlos|rand]] | ||
| + | *'''Bewehrungsauswahl''' | ||
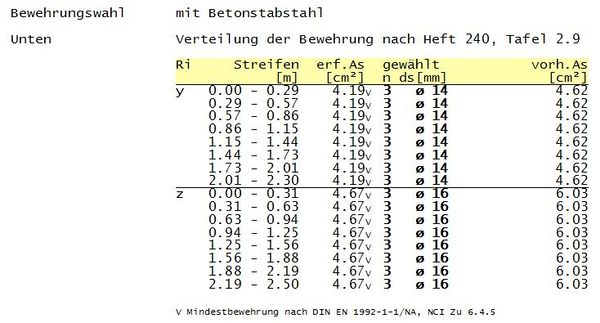
| + | ::*In der Handrechnung wurde eine Einteilung von 4 Streifen vorgenommen, mb hat mit 8 gerechnet (nach Heft 240 Tafel 2.9<ref name = "Q2">Deutscher Ausschuss für Stahlbeton - Heft 240, Tafel 2.9</ref>) | ||
| + | ::*Dadurch entstehen Abweichungen in der Bewehrungsmenge. | ||
| + | ::*Eine überschlägige Kontrolle der Handrechnung bekommt man, indem man jeweils die Bewehrungsmenge von 2 Streifen der mb-Rechnung addiert. | ||
| + | ::*Dadurch ergibt sich: | ||
| + | :::in y-Richtung | ||
| + | ::::Randbereich: 8,38 cm² | ||
| + | ::::Mittelbereich: 8,38 cm² | ||
| + | :::in z-Richtung | ||
| + | ::::Randbereich: 9,34 cm² | ||
| + | ::::Mittelbereich: 9,34 cm² | ||
| + | [[Datei: Beispiel_Fundamentberechnung_inkl_Durchstanzen_(S510.de)_30.JPG|600px|tumb|rahmenlos|rand]] | ||
| + | <div style="border: 2px solid blue; padding: 5px;">'''Hinweis:'''<br /> | ||
| + | *Bei der '''Bewehrungsanordnung''' treten Differenzen zwischen der Handrechnung und dem Vorschlag bei mb auf. | ||
| + | *Der Abstand der Bewehrungsreihen '''s<sub>w</sub>''' lässt sich eingeben, findet jedoch keine sichtliche Berücksichtigung bei der Bewehrungsanordnung bei mb. | ||
| + | *Auf die '''Mindestbewehrung zur Sicherstellung der Duktilität''' wird bei mb verzichtet, da ein duktiles Bauteilverhalten durch Umlagerung des Sohldrucks sichergestellt werden kann.<br /> | ||
| + | :Diese Umlagerungen ermöglichen i.d.R. neue Gleichgewichtszustände bei zunehmenden Verformungen, so dass ein Sprödbruch nicht zu erwarten ist.<ref name = "Q2"></ref> | ||
| + | </div><br /> | ||
| + | <br /> | ||
==Quellen== | ==Quellen== | ||
Aktuelle Version vom 17. Dezember 2015, 11:53 Uhr
| Stahlbetonbau • MB-AEC-Module Stahlbetonbau • Bemessung eines Einzelfundaments (Bsp.) |
Handrechnung
1.) Bewehrung in y-Richtung
- Ermittlung des Bemessungsmoments
- Aufgrund der monolithischen Verbindung zwischen Stütze und Fundament darf hier die Bemessung mit dem Anschnittmoment erfolgen.
- Für die Bemessung der Bewehrung in y-Richtung ist das Moment Mz maßgebend (Indizierung – Balkenmomente).
- Bodenauflast und Fundamenteigengewicht verursachen keine Biegemomente und werden daher bei der Berechnung nicht berücksichtigt.
_5.JPG)
- Querschnittsgeometrie
- Annahme: ØL = 14 mm (einlagig), die y-Bewehrung ist die untere Lage
- Da das Fundament direkt auf eine Sauberkeitsschicht betoniert wird, muss das Vorhaltemaß c um 20 mm vergrößert werden (Schneider, Kap. 5, Abschn. 5.1.2)[1]
_6.JPG)
- Biegebemessung
_7.JPG)
- Verteilung der Bewehrung nach Hahn
- 4 Bereiche mit b = 2,3/4 = 0,575 m
_8.JPG)
- Mittelbereiche
_9.JPG)
- Randbereiche
_10.JPG)
- Mindestbewehrung zur Sicherstellung der Duktilität
- Die Ermittlung der Bewehrungsmenge erfolgt für den 1m-Streifen.
- Der Hebelarm der inneren Kräfte wird vereinfachend mit z = 0,9d ermittelt.
_11.JPG)
- Bewehrungsauswahl
- Mittelbereiche: Ø 14, s = 11 cm (as,vorh = 13,99 cm²/m)
- Randbereiche: Ø 14, s = 19 cm (as,vorh = 8,10 cm²/m)
2.) Bewehrung in z-Richtung
- Ermittlung des Bemessungsmoments
_12.JPG)
- Querschnittsgeometrie
- Annahme: ØL = 14 mm (einlagig), die z-Bewehrung ist die obere Lage
_13.JPG){kind=small}
- Biegebemessung
_14.JPG)
- Verteilung der Bewehrung nach Hahn
- 4 Bereiche mit b = 2,5/4 = 0,625 m
_15.JPG)
- Mittelbereiche
_16.JPG)
- Randbereiche
_17.JPG)
- Mindestbewehrung zur Sicherstellung der Duktilität
_18.JPG)
- Bewehrungsauswahl
- Mittelbereiche: Ø 14, s = 11 cm (as,vorh = 13,99 cm²/m)
- Randbereiche: Ø 14, s = 19 cm (as,vorh = 8,10 cm²/m)
mb-Vergleichsrechnung
- Biegebemessung
- Die Bemessungsmomente für die y- und z-Richtung (Mz,d,max und My,d,max) stimmen mit der Handrechnung überein.
- MEd,z = 568,58 kNm 567,63 kNm = Mz,d,max
- MEd,y = 618,02 kNm 616,99 kNm = My,d,max
_29.JPG)
- Bewehrungsauswahl
- In der Handrechnung wurde eine Einteilung von 4 Streifen vorgenommen, mb hat mit 8 gerechnet (nach Heft 240 Tafel 2.9[2])
- Dadurch entstehen Abweichungen in der Bewehrungsmenge.
- Eine überschlägige Kontrolle der Handrechnung bekommt man, indem man jeweils die Bewehrungsmenge von 2 Streifen der mb-Rechnung addiert.
- Dadurch ergibt sich:
- in y-Richtung
- Randbereich: 8,38 cm²
- Mittelbereich: 8,38 cm²
- in z-Richtung
- Randbereich: 9,34 cm²
- Mittelbereich: 9,34 cm²
_30.JPG)
Hinweis:
- Bei der Bewehrungsanordnung treten Differenzen zwischen der Handrechnung und dem Vorschlag bei mb auf.
- Der Abstand der Bewehrungsreihen sw lässt sich eingeben, findet jedoch keine sichtliche Berücksichtigung bei der Bewehrungsanordnung bei mb.
- Auf die Mindestbewehrung zur Sicherstellung der Duktilität wird bei mb verzichtet, da ein duktiles Bauteilverhalten durch Umlagerung des Sohldrucks sichergestellt werden kann.
- Diese Umlagerungen ermöglichen i.d.R. neue Gleichgewichtszustände bei zunehmenden Verformungen, so dass ein Sprödbruch nicht zu erwarten ist.[2]
Quellen
Seiteninfo 
|