Schubkraftübertragung in Fugen: Unterschied zwischen den Versionen

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen
Zeile 74: Zeile 74:
 
<math>\nu_{Rdi} \le \nu_{Rdi,max}</math>
 
<math>\nu_{Rdi} \le \nu_{Rdi,max}</math>
  
−
<math>\nu_{Rdi,max}= 0,5\cdot \nu \cdot f_{cd}\cdot b_{i}</math>
+
<math>\nu_{Rdi,max}= 0,5\cdot \nu \cdot f_{cd}</math>
  
 
==Quellen==
 
==Quellen==

Version vom 2. Mai 2016, 11:54 Uhr

Grundlagen

An nebeneinander betonierten Ortbetonteilen oder an sogenannten Halbfertigteilen mit Ortbetonergänzung,

entstehen Verbundfugen, über die im Endzustand Schubbeanspruchungen zwischen den Teilen übertragen werden müssen.

An Trägern dieser Art müssen alle Nachweise am zusammengesetzten Querschnitt und zusätzlich der Nachweis der Schubkraftübertragung in der Fuge geführt werden.


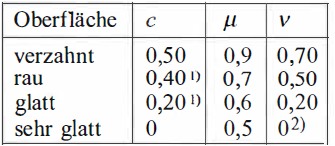
Fugen werden anhand ihrer Rauigkeit unterschieden. Es werden 4 Rauigkeitskategorien definiert: [1]


  • sehr glatt: Betonteil gegen glatte Oberfläche betoniert, unbehandelte Oberfläche, die aus sehr fließfähigem Beton Hergestellt wurde
  • glatt: abgezogene oder im Extruderverfahren hergestellte Betonoberfläche; ohne weitere Behandlung nach der Verdichtung
  • rau: mindestens 3mm Rauigkeit mit 40mm Zinkenabstand; mindestens 3mm freigelegte Gesteinskörnung
  • verzahnt: planmäßig hergestellte Geometrie; mindestens 6mm freigelegte Gesteinskörnung bei einer Mindestkörnung von d>= 16mm


Den einzelnen Rauigkeitskategorien werden Beiwerte nach folgender Tabelle zugeordnet:

Fugenbeiwerte.PNG

-Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c} - Rauigkeitsbeiwert

-Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} – Schubreibungsbeiwert

-Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu} – Abminderungsbeiwert

Nachweisführung

Der zu erfüllende Nachweis der aufnehmbaren Schubkraft lautet:[2]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Edi}\le \nu_{Rdi} \le \nu_{Rdi,max}}


Der Bemessungswert der aufzunehmenden Schubkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Edi}} ergibt sich zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Edi}= \beta \cdot \cfrac{V_{Ed}}{(z\cdot b_{i})}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =} Verhältnis von der Normalkraft in der Ortbetonergänzung zu der Gesamtnormalkraft; liegt die Fuge in der Zugzone ⇒ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =1,0} ; liegt sie in der Druckzone ⇒ Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta= \cfrac{F_{cdj}}{F_{cd}} \le 1,0 }

Anteil von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle F_{cd}} der über der Nulllinie liegt.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{i}} Breite der Fuge


Der Bemessungswert der aufnehmbaren Schubkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi}} setzt sich aus zwei Anteilen zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi}= \nu_{Rdi,c} + \nu_{Rdi,s}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi,c}} – Traglastanteil der unbewehrten Fuge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi,s}} – Traglastanteil der Fugenbewehrung


Der Traglastanteil der unbewehrten Fuge setzt sich aus dem Bemessungswert der Betonzugfestigkeit, den Spannungen infolge der äußeren Längskraft und den dazugehörigen Beiwerten zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi,c}= c\cdot f_{ctd} + \mu \cdot \sigma_{n}}

Der Lastanteil der Fugenbewehrung hängt von der Querschnittsfläche der, die Fuge kreuzenden, Bewehrung, der Stahlstreckgrenze und dem Winkel der Querkraftbewehrung ab.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi,s}= \cfrac{A_{s}}{A_{i}}\cdot f_{yd}\cdot (1,2\cdot \mu \cdot sin\alpha + cos\alpha)}

wobei:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}} - Querschnittsfläche der Bewehrung die die Fuge kreuzt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{i}} - Fläche der Fuge, über die Schub übertragen wird


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi} \le \nu_{Rdi,max}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rdi,max}= 0,5\cdot \nu \cdot f_{cd}}

Quellen

  1. ↑ Deutscher Ausschuss für Stahlbeton, Heft 600, Erläuterungen zu DIN EN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode 2), Berlin, 2012
  2. ↑ Schneider Bautabellen für Ingenieure, 20. Auflage, Köln: Werner Verlag, 2012
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Schubkraftübertragung_in_Fugen&oldid=7110“