Momentenumlagerung (Bsp.): Unterschied zwischen den Versionen
| Zeile 90: | Zeile 90: | ||
<br /> | <br /> | ||
[[File:Momentenumlagerung (Bsp.) 3.png|rahmenlos|rand|tumb|700px|Ausdruck vom Modul S340.de]]<br /> | [[File:Momentenumlagerung (Bsp.) 3.png|rahmenlos|rand|tumb|700px|Ausdruck vom Modul S340.de]]<br /> | ||
| + | <br /> | ||
==Beispiel 2 <small>Fehlerhafter Ausdruck bei Beton ≥ C 55/67</small>== | ==Beispiel 2 <small>Fehlerhafter Ausdruck bei Beton ≥ C 55/67</small>== | ||
| − | Das folgende Beispiel zeigt | + | Das folgende Beispiel zeigt einen Ausschnitt aus einer mit dem Modul S340.de durchgeführten Bemessung eines Stahlbeton-Durchlaufträgers. Am Stützmoment erfolgte eine Momentenumlagerung. |
| + | === Eingabeparameter === | ||
| + | Es werden nur relevante Eingabeparameter vorgegeben. <br /> | ||
| + | |||
| + | <math>M_\mathrm{Ed,1}=85{,}66\,\mathrm{kNm}~~~~\mathrm{massgebend}</math> <br /> | ||
| + | |||
| + | <math>M_\mathrm{Ed,B}=-114{,}23\,\mathrm{kNm}</math> <br /> | ||
==Quellen== | ==Quellen== | ||
=== Literaturverzeichnis === | === Literaturverzeichnis === | ||
Version vom 23. März 2015, 09:52 Uhr
Beispiel 1 maximale Umlagerung des Stützmoments
Das folgende Beispiel zeigt eine Momentenumlagerung des Stützmoments, wie Sie mit dem Modul S340.de geführt wird.
Aufgabe
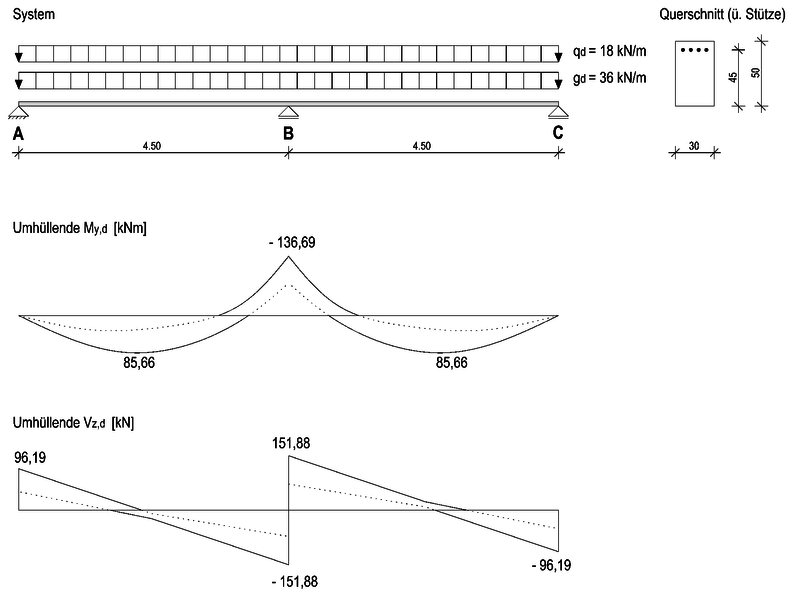
Ermittlung der Momentengrenzlinie für eine größtmögliche Umlagerung des Stützmoments über einer frei drehbaren Lagerung, für einen Stahlbetonträger mit folgendem System:
Vorgabewerte
Schnittgrößen wurden aus einer Rechnung von dem Modul S340.de übernommen:
(Es werden nur relevante Einwirkungskombinationen (EK) und deren Schnittgrößen vorgegeben.)
EK 2: (qd im Feld 1)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,1}=85{,}66\,\mathrm{kNm}~~~~\mathrm{massgebend}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B}=-114{,}23\,\mathrm{kNm}}
EK 5: (qd im Feld 2)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,1}=51{,}11\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B}=-114{,}23\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,2}=85{,}66\,\mathrm{kNm}~~~~\mathrm{massgebend}}
EK 6: (qd im Feld 1 und 2)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,1}=76{,}63\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B}=-136{,}69\,\mathrm{kNm}~~~~\mathrm{massgebend}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,2}=76{,}63\,\mathrm{kNm}}
Auflagerbreite:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t=0{,}24\,\mathrm{m}}
Berechnung
Lineare Berechnung mit Begrenzter Umlagerung
Bestimmung des zulässigen Umlagerungsfaktors, mit dem Eingangswert des bezogenen Moments vor der Umlagerung.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_\mathrm{Eds}=\frac {M_\mathrm{Eds}}{b\cdot d^2\cdot f_\mathrm{cd}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{cd}=\alpha_\mathrm{cc}\cdot f_\mathrm{ck}/\gamma_\mathrm{C}~~~\mathrm{(i.~Allg.~gilt~\alpha_\mathrm{cc}=0{,}85)}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{cd}=0{,}85\cdot 20\,\mathrm{Nmm^{-2}}/1{,}5=11{,}33\,\mathrm{Nmm^{-2}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_\mathrm{Eds}=\frac {136{,}69\,\mathrm{kNm}\cdot 10^{-3}}{0{,}30\,\mathrm{m}\cdot (0{,}45\,\mathrm{m})^2 \cdot 11{,}33\,\mathrm{Nmm^{-2}}}=\underline{0{,}1986}}
Zur Veranschaulichung, wird der zulässige Umlagerungsfaktor δ aus dem unten stehenden Diagramm entnommen.
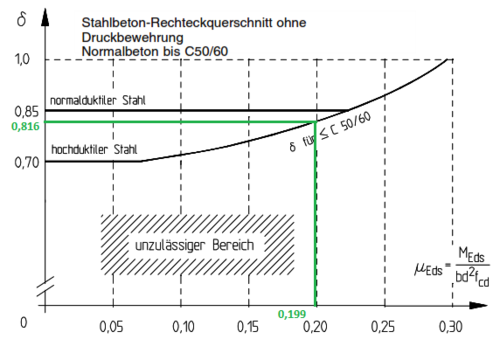
Bild: Zulässiger Umlagerungsfaktor δ [Goris-2013/2]
Wert des Umlagerungsfaktors bei einer Betonfestigkeitsklasse von C20/25:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to \delta=0{,}816}
Da der Umlagerungsfaktor abhängig von der Duktilität des verwendeten Stahls ist, wird im folgenden unterschieden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to \delta=\underline{0{,}85}~~~\mathrm{fuer~B~500~A~(normalduktil)}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to \delta=0{,}816~~\mathrm{fuer~B~500~B~(hochduktil)}}
Das Stützmoment wird um 15% vermindert:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B,\delta =0{,}85}=0{,}85\cdot (-136{,}69)=\underline{\underline{-116{,}19\,\mathrm{kNm}}}}
Da das umgelagerte Stützmoment |MEd,B|=116,19 kNm in der Einwirkungskombination 6 (qd im Feld 1 und 2) betragsmäßig größer als das Stützmoment |MEd,B|=114,23 kNm in der Einwirkungskombination 2 bzw. 5 (qd im Feld 1 bzw. 2) ist, bleibt für weitere Berechnungen das Feldmoment |MEd,1,2|=85,66 kNm in der Einwirkungskombination 6 (qd im Feld 1 und 2) maßgebend.
Der Querkraftverlauf ergibt sich aus den Gleichgewichtsbedingungen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,A}=\cfrac{(g_\mathrm{d}+g_\mathrm{d})\cdot x}{2}+\cfrac{\vert M_\mathrm{Ed,1}\vert}{x}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,1}\vert=85{,}66\,\mathrm{kNm}~~~~\mathrm{(an~der~Stelle~x=1{,}80\,\mathrm{m})}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,A}=\cfrac{(36\,\mathrm{kNm^{-1}}+18\,\mathrm{kNm^{-1}})\cdot 1{,}80\,\mathrm{m}}{2}+\cfrac{85{,}66\,\mathrm{kNm}}{1{,}80\,\mathrm{m}}=\underline{\underline{96{,}19\,\mathrm{kN}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,B}=\cfrac{(g_\mathrm{d}+g_\mathrm{d})\cdot x}{2}+\cfrac{\vert M_\mathrm{Ed,B}\vert}{x}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,B}\vert=116{,}19\,\mathrm{kNm}~~~~\mathrm{(an~der~Stelle~x=4{,}50\,\mathrm{m})}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,B}=\cfrac{(36\,\mathrm{kNm^{-1}}+18\,\mathrm{kNm^{-1}})\cdot 4{,}50\,\mathrm{m}}{2}+\cfrac{116{,}19\,\mathrm{kNm}}{4{,}50\,\mathrm{m}}=\underline{\underline{147{,}32\,\mathrm{kN}}}}
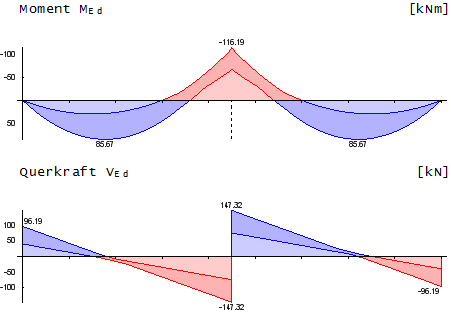
Vergleich mit mb-AEC Baustatik
In der Ausgabe vom Modul S340.de, erscheint folgender Ausdruck:
Beispiel 2 Fehlerhafter Ausdruck bei Beton ≥ C 55/67
Das folgende Beispiel zeigt einen Ausschnitt aus einer mit dem Modul S340.de durchgeführten Bemessung eines Stahlbeton-Durchlaufträgers. Am Stützmoment erfolgte eine Momentenumlagerung.
Eingabeparameter
Es werden nur relevante Eingabeparameter vorgegeben.
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle M_{\mathrm {Ed,1} }=85{,}66\,\mathrm {kNm} ~~~~\mathrm {massgebend} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B}=-114{,}23\,\mathrm{kNm}}
Quellen
Literaturverzeichnis
- [Goris-2013/2] Goris, A.: Stahlbeton-Praxis nach Eurocode 2. Band 2: Schnittgrößen, Gesamtstabilität, Bewehren und Konstruktion, Brandbemessung nach DIN EN 1992-1-2, Beispiele. 5. Auflage, Beuth/Bauwerk Verlag, Berlin 2013, ISBN 978-3-410-23734-1
Sonstiges
- Modul-Version: 2014.011
- Autor: R. Wengatz
- Veröffentlicht am: 24.02.2015
- Status: in Bearbeitung