Adaptive Tragwerke: Unterschied zwischen den Versionen
| (115 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
<br /> | <br /> | ||
| − | + | Als '''adaptive Tragwerke''' (von lateinisch ''adaptare'' "anpassen") bezeichnet man Systeme, die in der Lage sind, sich ihrer Umgebung und den äußeren Einflüssen anzupassen und auf diese angemessen zu reagieren. Es entsteht in gewisser Weise ein Wechselspiel zwischen der Umgebung und dem Tragwerk selbst, welches zu einer Optimierung von vorher festgelegten Eigenschaften und Zielen führt. Ziel solcher Tragwerksentwürfe ist es, dass das System mittels aktiver Elemente in der Lage ist, auf unterschiedliche Situationen und Lastfälle zu reagieren und sich anzupassen. Durch die Integration aktiver Elemente können in der Bemessung auftretende Steifigkeitsprobleme in Festigkeitsprobleme überführt werden. Hier ergibt sich ein entscheidender Vorteil hinsichtlich Masseneinsparung, sodass Überdimensionierungen verhindern werden können. | |
| − | |||
| − | Als '''adaptive Tragwerke''' bezeichnet man Systeme, die in der Lage sind, sich ihrer Umgebung und den äußeren Einflüssen anzupassen und auf diese angemessen zu reagieren. Es entsteht in gewisser Weise ein Wechselspiel zwischen der Umgebung und dem Tragwerk selbst, welches zu einer Optimierung von vorher festgelegten Eigenschaften und Zielen führt. | ||
| − | + | Der Ursprung solcher Systeme ist auf die Natur zurückzuführen. Chamäleons sind in der Lage, sich farblich ihrer Umgebung anzupassen, um sich vor Feinden zu schützen. Dieses Prinzip der Anpassung kann auch die Technik übertragen werden. Bereits in der Luft- und Raumfahrt Technik, in der Automobilbranche und auch in der Optik lassen sich unterschiedliche adaptive Systeme wiederfinden (automatisch einfahrbare Tragflächen Flugzeug, adaptive Fahrwerke, adaptive Optik). | |
| − | Allgemein werden adaptive Systeme | + | Die Idee adaptiver Tragwerke im Bauwesen besteht darin, Material einzusparen und durch externe Energie zu "ersetzen". |
| + | Allgemein werden adaptive Systeme unterschieden in: aktiv und passiv. Teilweise wird in der Wissenschaft auch von Hybridsystemen gesprochen.<br /> | ||
| − | |||
| − | + | ==Ziele und Gründe für Adaption== | |
| − | + | Mit Blick auf die aktuellen sozialen Probleme wie die Entwicklung der wachsenden Weltbevölkerung, der herrschender Materialknappheit und dem Klimawandel ist ein Umbruch vor allem in der Baubranche zwingend notwendig. Die Baubranche macht derzeit mehr als 50% der globalen Ressourcennutzung und rund 1/3 der globalen CO2 Emissionen aus. Ressourcenschonendes und wirtschaftliches Entwerfen und Konstruieren von Bauwerken waren schon immer ein Bestreben im Ingenieurwesen gewesen und gewinnen aktuell und in Zukunft noch mehr an Bedeutung. Dafür sind neue Entwurfsansätze zwingend notwendig. | |
| − | + | Mittels adaptiver Tragwerke können folgende Optimierungsziele verfolgt werden: <ref name = "Q1"> Pawlowski, Robert: Adaptive Dachtragwerke – Entwicklung eines Entwurfsverfahrens – Betrachtung ausgewählter Aspekte. Dissertation: Technische Universität München, 2006 </ref>: | |
| + | *Verringerung von Verformungen | ||
| + | *Höhere Tragfähigkeiten | ||
| + | *Optimierung des Schwingungsverhalten | ||
| + | *Reduzierung des Ressourcen- und Energieverbrauchs | ||
| + | *Größere Spannweiten und höhere Konstruktionen | ||
| + | *Mehr Komfort bei der Nutzung (bezogen auf die Raumqualität und Adaption von Fassaden) | ||
| + | *Verlängerung der Lebensdauer | ||
=Systemübersicht und Elemente= | =Systemübersicht und Elemente= | ||
| − | [[File: | + | [[File:AdaptiveTragwerke1.png|right|thumb|450px|Grundlegende Struktur und Systemablauf adaptiver Systeme (nach Weber <ref name = "Q2"> Weber, Christian-Toralf: Ein Beitrag zur optimalen Positionierung von Aktoren in adaptiven mechanischen Strukturen, Düsseldorf: VDI, 1998 </ref>) ]] |
Durch das Integrieren von multifunktionalen Bauteilen entstehen intelligente und dadurch anpassungsfähige Systeme. Infolge der Anpassungsfähigkeit, <br/> | Durch das Integrieren von multifunktionalen Bauteilen entstehen intelligente und dadurch anpassungsfähige Systeme. Infolge der Anpassungsfähigkeit, <br/> | ||
| Zeile 26: | Zeile 30: | ||
Solche Systeme bestehen allgemein aus den folgenden drei Komponenten: | Solche Systeme bestehen allgemein aus den folgenden drei Komponenten: | ||
| − | *''' | + | *'''Sensoren:''' zur kontinuierlichen Messung äußerer Einflüsse oder systeminterner Zustände (z.B. Dehnungsmessstreifen usw.) |
| − | *''' | + | *'''Steuerung und Regelung:''' Verarbeitung der von den Sensoren gemessenen Information und Weitergabe an Aktuatoren |
| − | + | *'''Aktuatoren:''' Ausführungselement der notwendigen Adaption (z.B. Hydraulikzylinder) | |
| + | |||
| + | |||
| + | ==Sensoren== | ||
| + | |||
| + | Den Sensoren ist die Aufgabe der Übertragung von Informationen zuzuordnen. Sie sind in der Lage, Veränderungen der Systemeinflüsse wahrzunehmen und den internen Zustand des Systems kontinuierlich zu messen.<ref name = "Q3"> Teuffel, Patrick: Entwerfen adaptiver Strukturen, Lastpfadmanagement zur Optimierung tragender Leichtbaukonstruktionen. Dissertation: Universität Stuttgart, 2004 </ref> Ein Sensor ist somit das erste Element in der Reihenfolge adaptiver Systeme. Im Allgemeinen erzeugen die Sensoren ein elektrisches Ausgangssignal, welches an die Steuerung bzw. Regelung weitergegeben wird. Dort wird es verarbeitet, umgewandelt und dann an die Aktuatoren des Systems weitergeleitet. <ref name = "Q4"> | ||
| + | Isermann, Rolf: Mechatronische Systeme: Grundlagen, Berlin, Heidelberg, New York: Springer-Verlag, 1999 </ref> <br /> | ||
| + | |||
| + | Zu den an den häufigsten verwendeten Sensoren gehören die Dehnungsmessstreifen (kurz DMS), welche zur Messung von Dehnungen geeignet sind und somit ein typisches Beispiel der “Wegmessung“ darstellen. | ||
| + | |||
| + | ==Steuerung und Regelung== | ||
| + | |||
| + | Bei adaptiven Systemen wird in Steuerung und Regelung differenziert. Der Unterschied bei der Anwendungen liegt darin, dass bei einer Steuerung lediglich die äußeren Einflüsse ermittelt werden, während bei der Regelung Systemantworten generiert werden. Dementsprechend spricht man bei der Abhängigkeit zur Optimierung durch äußere Lasten von Steuerung und bei Systemverformungen oder der Variation der Systemeigenschaften von Regelung. Das bedeutet, dass eine Regelung zur Ausführung der Adaption innerhalb eines Systems unabdingbar ist.<ref name = "Q1"></ref> | ||
| + | |||
| + | ==Aktuatoren== | ||
| + | |||
| + | Die Aktuatoren oder Aktoren in einem System lassen sich auch als “Stellgrößen“ bezeichnen. Sie sind dafür zuständig, die von der Steuerung bzw. Regelung übertragenden Signale und Informationen umzusetzen und somit die Adaption auszuführen. Sie bilden daher das Gegenstück bzw. Bindeglied zu den Sensoren. <br /> | ||
| + | |||
| + | Die Aktuatoren eines Systems transformieren dabei elektrische Signale in mechanische oder chemische Größen.<ref name = "Q3"></ref> Für die Umsetzung dieser technischen Prozesse ist meistens eine elektrische, hydraulische oder pneumatische Hilfsenergie erforderlich. Da Aktuatoren keine dauerhafte Arbeit leisten müssen, sondern nur kurzfristig zum Einsatz kommen, müssen diese Elemente bestimmte Anforderungen erfüllen <ref name = "Q4"></ref>: | ||
| + | |||
| + | *Möglichst lineare bzw. statische Übertragungseigenschaften | ||
| + | *Funktionen Antreiben und Bremsen | ||
| + | *Hohe Belastbarkeit | ||
| + | *Möglichkeit zur genauen Positionierung | ||
| + | *Schnelle, gut gedämpfte dynamische Eigenschaften | ||
| + | *Geeignete Schnittstellen für Sensoren | ||
| + | |||
| + | Im Allgemeinen können Aktuatoren für verschiedene Aufgaben eingesetzt werden. Die Aktuatoren werden dabei in Kategorien nach dem jeweiligen technischen Prozess bzw. nach den notwendigen Hilfsenergien unterteilt. | ||
| + | |||
| + | ==Passive Systeme== | ||
| + | |||
| + | [[File:AdaptiveTragwerke2.png|right|thumb|300px|Funktionsprinzip passiver Systeme (in Anlehnung <ref name = "Q6"></ref>) ]] | ||
| + | Bei der '''passiven Adaption''' reagieren die Systeme direkt auf die Einflüsse '''ohne''' jeglichen Einsatz von Steuerung durch zum Beispiel Sensoren. </br> | ||
| + | Somit ist eine Zuwendung externer Energie nicht notwendig. Bei passiven Systemen wird die Bewegung und Dynamik des Tragwerkes selbst genutzt und die dadurch entstandene Energie absorbiert.<ref name = "Q5"> Symans, M. D.; et al.: Semi-active control systems for seismic protection of structures: a state-of-the-art review. In: Engineering structures 21, Seiten 469-487 </ref> </br> | ||
| + | Typische Beispiele passiver Adaption sind Feder-Masse-Systeme, die als Schwingungstilger oder –Dämpfer, die auf das Tragwerk einwirkende Energie aufnehmen und diese in eine Relativbewegung <br /> | ||
| + | zur Absorption umwandeln können. Denkbar sind auch Systeme, die frei drehbar sind und sich beispielsweise der jeweiligen Windrichtung anpassen können. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <br /> | ||
| + | |||
| + | ==Aktive Systeme== | ||
| + | |||
| + | [[File:AdaptiveTragwerke3.png|right|thumb|300px|Funktionsprinzip aktiver Systeme (in Anlehnung <ref name = "Q6"></ref>) ]] | ||
| + | Im Gegensatz zur passiven Adaption ist bei einer '''aktiven Adaption''' das Aufbringen '''externer Energie''' zur Aktivierung der Steuerung notwendig.</br> | ||
| + | Die Aktivierung wird durch zusätzliche Sensoren ausgelöst, gesteuert und durch die integrierten Aktuatoren umgesetzt. Häufig kommen an dieser Stelle elektrohydraulische oder elektromechanische Aktuatoren zum Einsatz.<ref name = "Q5"></ref> Ein Vorteil der aktiven Adaption mit dieser Steuerung ist eine größere Abdeckung der Anpassungsfähigkeit der Systeme. Die Reaktionen und möglichen Steuerungen dieser Systeme sind deutlich weitreichender. Aktive Systeme werden häufig dazu eingesetzt, um die jeweiligen Zustandsgrößen (Verformungen und innere Kräfte) zu beeinflussen.<ref name = "Q6"> Bretz, A.; Calmano, S. et al.: Darstellung passive, semi-aktiver und aktiver Systeme auf Basis eines Prozessmodells, SFB 805, TU Darmstadt </ref> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <br /> | ||
| + | |||
| + | ==Semi-aktive Systeme== | ||
| + | |||
| + | [[File:AdaptiveTragwerke4.png|right|thumb|300px|Funktionsprinzip semi-aktiver Systeme (in Anlehnung <ref name = "Q6"></ref>) ]] | ||
| + | '''Semi-aktive Systeme''' sind eine Kombination aus aktiven und passiven Systemen, bei denen die Vorteile beider Systeme kombiniert genutzt werden.<ref name = "Q1"></ref> Bei diesen Systemen wird die Adaption durch eine '''Manipulation der jeweiligen Systemeigenschaft''' (z.B. der Steifigkeit oder durch Dämpfung) hervorgerufen. Semi-aktive Systeme sind auch auf eine externe Energiequelle angewiesen. Allerdings ist die notwendige Hilfsenergie deutlich geringer als bei aktiven Systemen, dabei wird die Anpassungsfähigkeit jedoch nicht beeinträchtigt.<ref name = "Q1"></ref> Semi-aktive Regelsysteme werden vor allem zur Nutzung von Steifigkeitsregelungsgeräten, elektrorheologischen und magnetorheologischen Dämpfern oder abgestimmten Flüssigkeitsdämpfern erforscht.<ref name = "Q5"></ref> | ||
| + | |||
| + | |||
| + | |||
| − | + | <br /> | |
=Anwendung im Bauwesen= | =Anwendung im Bauwesen= | ||
| Zeile 39: | Zeile 102: | ||
*'''Systemkräfte''' und '''Lasteinleitung''', welche sowohl Schnittgrößen als auch Verformungen beeinflussen können. | *'''Systemkräfte''' und '''Lasteinleitung''', welche sowohl Schnittgrößen als auch Verformungen beeinflussen können. | ||
*Die '''Geometrie''' und '''maßgebende Formgebung''' des Tragwerks können bei der Aufnahme von Lasten eine entscheidende Stellgröße darstellen. | *Die '''Geometrie''' und '''maßgebende Formgebung''' des Tragwerks können bei der Aufnahme von Lasten eine entscheidende Stellgröße darstellen. | ||
| − | *Unterschiedliche '''Steifigkeiten''' von Einzelelementen oder auch von Bereichen innerhalb des Systems können ebenfalls zu einer Reduzierung der Schnittkräfte führen. Durch Steifigkeiten können somit bestimmte veränderliche Einwirkungen homogenisiert werden. | + | *Unterschiedliche '''Steifigkeiten''' von Einzelelementen oder auch von Bereichen innerhalb des Systems können ebenfalls zu einer Reduzierung der Schnittkräfte führen. Durch Steifigkeiten können somit bestimmte veränderliche Einwirkungen homogenisiert werden.<ref name = "Q1"></ref> |
*Ähnlich wie die Steifigkeit kann auch die '''Masse''' eines Systems eine entscheidende Rolle zur Adaption der Tragwerke besitzen und zur Lastaufnahme beitragen. | *Ähnlich wie die Steifigkeit kann auch die '''Masse''' eines Systems eine entscheidende Rolle zur Adaption der Tragwerke besitzen und zur Lastaufnahme beitragen. | ||
| Zeile 46: | Zeile 109: | ||
==Verformungsadaption== | ==Verformungsadaption== | ||
| − | Bei der '''Verformungsadaption''' | + | Bei der '''Verformungsadaption''' sollen ermittelte Verformungen oder Verschiebungen optimiert werden. Dazu müssen zunächst die erforderlichen Dehnungen, Längenänderungen und Arbeiten der einzelnen Elemente ermittelt werden. Nachfolgend können die Kräfte zur Verhinderung dieser Verschiebungen ermittelt werden. Diese müssen dann für die Adaption entgegenwirken, um die Verformungen somit zu homogenisieren. Teilweise können auch Verformungen eines Systems zur Optimierung vorgegeben werden (z.B. Überhöhung bei Brücken). (Beispiel: Stuttgarter Träger) |
==Schnittgrößenadaption== | ==Schnittgrößenadaption== | ||
| − | '''Schnittgrößen-''' oder auch '''Momentenadaption''' genannt, hat zum Ziel die Schnittgrößen eines Systems durch z.B. Änderung der Steifigkeit oder Lasteinleitung zu homogenisieren. | + | '''Schnittgrößen-''' oder auch '''Momentenadaption''' genannt, hat zum Ziel die Schnittgrößen eines Systems durch z.B. Änderung der Steifigkeit oder Lasteinleitung zu homogenisieren. Auch die Formgebung des Gesamtsystems kann sich positiv auf die Schnittgrößen auswirken, z.B. kann die Struktur dem Momentenverlauf angepasst werden. Oftmals wird die Angleichung der Feld- und Stützmomente zum Optimierungsziel gewählt. Typische Anwendungen in der Baupraxis sind auch Systeme zur Dämpfung von dynamischen Lasten wie Schwingungen oder Erdbeben. (Beispiel: Thyssenkrupp Elevator Testturm) |
| − | Auch die Formgebung des Gesamtsystems kann sich positiv auf die Schnittgrößen auswirken, z.B. kann die Struktur dem Momentenverlauf angepasst werden. Oftmals wird die Angleichung der Feld- und Stützmomente zum Optimierungsziel gewählt. | + | |
| + | |||
| + | |||
| + | ===Steifigkeitsadaption=== | ||
| + | |||
| + | Die Steifigkeitsadaption gehört auch zu der Schnittgrößenadaption. Häufig wird bei der Schnittgrößenadaption jedoch auf die Formgebung des Tragwerks zur optimalen Lastaufnahme oder einer Schwingungsdämpfung gesprochen. Bei der Steifigkeitsadaption allerdings sollen das Tragwerk oder nur einzelne Bauteile in der Lage sein, ihre Steifigkeiten zu ändern, um somit beispielswiese innere Lasten oder auch Verformungen zu verringern. Durch die interne Änderung der Steifigkeiten können gewisse Beanspruchungszustände homogenisiert werden.<ref name = "Q7"> Sobek, Werner; Haase, Walter, et al.: Adaptive Systeme. In: Stahlbau 7/69, Berlin: Ernst & Sohn, 2000 </ref> “The Kajima Technical Research Institute“ wurde 1990 erbaut und ist das erste Gebäude mit veränderbaren Steifigkeiten. Bei diesem Gebäude können aus Erdbeben entstehende Horizontallasten optimal übertragen werden. Die Adaption erfolgt durch den Einsatz eines hydraulischen Systems, mit dem die Steifigkeit des Tragwerkes beeinflusst werden kann. Je nach Steifigkeit dieser Elemente variiert das statische System zwischen einem Fachwerk (steif) und einem Rahmen (weich) <ref name = "Q8"> Culshaw, Brian: Smart Structures and Materials, Boston, London: Artech House, 1996 </ref>, wodurch die Lastverteilung variiert werden kann. <br/> | ||
| + | Wie bereits erwähnt ist vor allem der Einsatz von semi-aktiven Regelsystemen zur Steifigkeitsadaption z.B. in Form von Steifigkeitsregelgeräten denkbar. Dabei dienen regelbare Steifigkeitsvorrichtungen der Aussteifung eines Systems bzw. Gebäudes vor allem unter Lasten, die durch Erdbeben entstehen. Ähnlich wie bei dem oben erwähnten Technical Research Institute werden dabei die Steifigkeitsvorrichtungen je Stockwerk eingeklinkt oder freigegeben. Es handelt sich dabei um einen Hydraulikzylinder (doppeltwirkende Kolbenstange) mit einem Magnetventil. Das Magnetventil verbindet die beiden Kammern und steuert somit den Flüssigkeitsstrom zum Aktivieren bzw. Deaktivieren der Aussteifung. Der Betrieb braucht in etwa eine Leistung von 20 W und eine Zeit von 30 ms.<ref name = "Q9"> Kobori T.; Takahashi M. et al.: Seismic response controlled structure with active variable stiffness system. In: Earthquake Engineering and Structural Dynamics, 1993 </ref> | ||
| + | |||
| + | =Einflüsse auf die Adaption eines Tragwerkes= | ||
| + | |||
| + | Um Adaptionsvorgänge von Systemen zu analysieren, muss die Varianz der Geometrie und das Tragverhalten des unbelasteten Tragwerks untersucht werden. Weiterhin müssen auch Betrachtungen aus Theorie 2. Ordnung hinzugezogen werden, da die Dehnungen und Stellwege der Aktuatoren einen großen Einfluss auf die Tragwerksverformungen haben können. Da während der Adaption einzelne Parameter oder teilweise die gesamte Geometrie des Grundsystems verändert werden, sind die einzelnen Systeme nicht konstant und werden de facto immer wieder neu definiert.<ref name = "Q1"></ref> | ||
| + | Im Wesentlichen wird der Optimierungsprozess sowohl durch den Zeitpunkt der Lastaufbringung als auch durch auftretende Tragwerksverformungen beeinflusst. Aber auch Faktoren wie die notwendige Adaptionsarbeit und einzuhaltende Sicherheitsanforderungen (Tragfähigkeit und Gebrauchstauglichkeit) sind dabei nicht zu vernachlässigen. Sie nehmen dabei einen wesentlichen Einfluss auf den Entwurf und die Berechnung adaptiver Tragwerke. Dazu muss vor allem die Einflussnahme der Geometrieänderungen des unbelasteten Tragwerkes untersucht werden. | ||
| + | |||
| + | ==Adaptionsarbeit== | ||
| + | |||
| + | Die Adaptionsarbeit bezeichnet den Aufwand, der zum Erreichen der Adaption notwendig ist. Die Adaptionsarbeit setzt sich zum einen aus der Arbeit der adaptierenden Kräfte als auch zum anderen aus dem Betrag des inneren Potentials des Tragwerks zusammen. Das innere Potential beschreibt dabei die Änderungen innerhalb des Systems während des Adaptionsprozesses. Dabei wird die Formänderungsarbeit innerhalb des Tragwerkes als Energie gespeichert und bei Entlastung wieder freigegeben. Durch die Adaption wird dieses Energiepotenzial der inneren Kräfte um den Betrag verändert.<ref name = "Q1"></ref> | ||
| + | |||
| + | Für die Ermittlung der Adaptionsarbeit sind neben den geometrischen Veränderungen und dem Zeitpunkt der Adaption weiterhin zwei Fallunterscheidungen zu betrachten: | ||
| + | *Störungsfreier Betrieb und | ||
| + | *Versagensfall | ||
| + | |||
| + | ==Einfluss des Zeitpunktes der Adaption== | ||
| + | |||
| + | Der Zeitpunkt der Lastaufbringung hat für die Adaption selbst und für die aufzubringende Adaptionsarbeit einen entscheidenden Einfluss. Dabei werden in der Theorie die folgenden '''drei Grenzfälle''' unterschieden: | ||
| + | |||
| + | '''Adaption vor der Lastaufbringung:''' <br/> | ||
| + | Das Adaptionsziel wird erst nach der Lastaufbringung erreicht, da die Geometrie im Vorfeld durch z.B. Vorspannungen (Schnittgrößenadaption) oder eine Überhöhung (Verformungsadaption) optimiert bzw. beeinflusst wird. Die erforderliche Adaptionsarbeit ist für diesen Grenzfall am kleinsten. | ||
| + | |||
| + | '''Adaption nach der Lastaufbringung:''' <br/> | ||
| + | Die Adaption findet erst nach der Lastaufbringung statt, sodass entgegen der Last gearbeitet werden muss. In diesem Fall ist die notwendige Adaptionsarbeit maximal. | ||
| + | |||
| + | '''Adaption während der Lastaufbringung:''' <br/> | ||
| + | In diesem Grenzfall erfolgt die Adaption des Tragwerkes nach Möglichkeit zeitgleich mit der Lastaufbringung. Diese Betrachtung stellt in der Praxis auch den Regelfall dar. Die erforderliche Adaptionsarbeit pendelt sich dabei zwischen den beiden zuvor genannten Grenzfällen ein.<ref name = "Q1"></ref> | ||
| + | |||
| + | ==Einfluss der Tragsicherheit und Gebrauchstauglichkeit== | ||
| + | |||
| + | Da Tragwerke in der Regel darauf ausgelegt sind, bestimmte Verformungen aufnehmen zu können, ohne zu versagen, ist eine vollständige Adaption der Verformungen auf null nicht immer sinnvoll. Außerdem müssen auch die Zusammenhänge der Schnittgrößen in den unterschiedlichen Zuständen eines Systems (passiv, aktiv und adaptiert) berücksichtigt werden. | ||
| + | |||
| + | Das Sicherheitskonzept adaptiver Tragwerke ist von großer Bedeutung, da es bei solchen Systemen zum Einsatz technischer Komponenten kommt. Es muss immer sichergestellt werden, dass das adaptive Tragwerk auch beim Ausfall der adaptiven Elemente nicht versagt. Die Gebrauchstauglichkeit kann dabei zunächst vernachlässigt werden. In Anlehnung an die bereits bekannten Sicherheitskonzepte aus dem Eurocode 0 zur Berechnung von Tragwerken, gibt es für den Entwurf von adaptiven Tragwerken unterschiedliche Herangehensweisen.<ref name = "Q1"></ref> | ||
| + | |||
| + | =Systemoptimierung= | ||
| + | |||
| + | Im Wesentlichen ist die Optimierung eines Systems hauptsächlich von den Auflagerbedingungen (Anzahl, Ort und Art der Auflager) und einer optimalen Stützweite abhängig. Dabei bestimmt die Anzahl der Auflager den Grad der statischen Unbestimmtheit. Die Anzahl und auch die Position der Auflager nehmen dabei einen entscheidenden Einfluss auf die Größen der Momente. Durch eine sinnvolle Anordnung kann ein ausgeglichener Momentverlauf mit in etwa gleich großen Maximal- und Minimalwerten erreicht werden. | ||
| + | Allgemein sollten die folgenden Anforderungen bei der Optimierung des Systems beachtet werden: | ||
| + | *Gleichmäßige Verteilung der Lasten, gegebenenfalls System von Beginn an optimieren hinsichtlich der Lasteinleitung und -verteilung | ||
| + | *Große Stützweiten vermeiden | ||
| + | *Statisch unbestimmte Systeme haben deutlich mehr Tragkapazitäten | ||
| + | *Die Anzahl der Auflager bzw. Federn können den Momentenverlauf maßgebend beeinflussen | ||
| + | |||
| + | ==Möglichkeiten der Steifigkeitsadaption== | ||
| + | |||
| + | Bei dem bereits aufgeführten Beispiel “The Kajima Technical Research Institute“ findet die Steifigkeitsadaption Anwendung, indem '''phasen- bzw. steifigkeitsverändernde Bauteile''' dazu genutzt werden, die Art des statischen Systems zu beeinflussen. Im Rahmen einer '''Master-Thesis''' mit dem Titel '''"Möglichkeiten der Steifigkeitsadaption bei statisch unbestimmten Trägersystemen"''' <ref name = "Q10"> Schwegmann, Lisa: Möglichkeiten der Steifigkeitsadaption bei statisch unbestimmten Trägersystemen, Master-Thesis: Hochschule Wismar, 2021</ref> wurden erste Berechnungsansätze zur Steifigkeitsadaption anhand von federgelagerten Systemen durchgeführt und untersucht. Federlagerungen werden im Bauwesen allgemein durch elastische Auflager oder Anschlüsse praktisch umgesetzt. Fundamente werden auch häufig als federgelagertes Systeme angesetzt, da so für den anstehenden Boden bzw. die Bettung eine gewisse Nachgiebigkeit berücksichtig werden kann. Solche Systeme haben aber nur begrenzte Kapazitäten und basieren auf zuvor getroffenen Annahmen. Dabei sind dann die Auflager oder auch der Boden nicht regelbar und in der Lage, gesteuert zu werden. | ||
| + | Bei der '''Adaption''' ist eine '''aktive Steuerung bzw. Regelung''' einzelner Elemente zur Abdeckung größerer Optimierungsspektren durch zum Beispiel semi-aktive Systeme denkbar. Die Aktuatoren (Federn) können aktiv gesteuert werden, um so auf die äußeren Einflüsse reagieren zu können und bessere Systemeigenschaften hervorzurufen. Dazu müssen ständige Messungen der momentanen Belastungen durchgeführt werden, um die Steifigkeiten der Federn in Abhängigkeit dazu zu justieren. Hierbei sind Sensoren wie Dehnungsmessstreifen (DMS) oder Kraftmesser denkbar. Aus der Summe der gemessenen Kräfte jedes Auflagers ergibt sich die Gesamtbelastung. Aus den Differenzen kann der Ort der Belastung ermittelt werden. Die ermittelten Kräfte können dann über die Sensoren an die Regeleinheit des Systems weitergegeben werden. Diese sendet dann die Information durch Signale an die Aktuatoren, welche die jeweils notwendige Adaption der Steifigkeiten durchführt. | ||
| + | |||
| + | ==Berechnungsansätze== | ||
| + | |||
| + | [[File:AdaptiveTragwerke6.png|right|thumb|450px|Übersicht der untersuchten Systeme <ref name = "Q10"></ref>]] | ||
| + | In der erwähnten Master-Thesis <ref name = "Q10"></ref> wurden verschiedene Zusammenhänge der Steifigkeitsadaption unter der Verwendung von Federn durch eine Parameteruntersuchung herausgearbeitet. | ||
| + | Je steifer die Feder eingestellt wird, desto “anziehender“ wirkt diese auf die einwirkenden Kräfte und fungiert wie ein festes Auflager. Bei weicheren Federn können dementsprechend weniger Kräfte aufgenommen werden und auch die Verformungen sind an dieser Stelle größer. | ||
| + | Um die jeweiligen Einflüsse der unterschiedlichen Stellgrößen innerhalb eines Systems zu untersuchen und zu beurteilen, wurden die Parameter isoliert voneinander betrachtet. Dabei wurden unterschiedliche Systeme untersucht. Die nebenstehende Abbildung zeigt den grundsätzlichen Aufbau des untersuchten Systems. Es wurden sowohl '''zwei-Feld-Träger''' mit einer Feder als als auch '''drei-Feld-Träger''' mit zwei Federn untersucht, bei denen die Federn jeweils in ihrer Federsteifigkeit kF variiert wurden. Weiterhin wurde der Sonderfall einer "negativen" Federsteifigkeit durch eine nach oben gerichtete Kraft simuliert. Auch die Varianz der Laststellungen wurden im Anschluss daran betrachtet. | ||
| + | |||
| + | |||
| + | |||
| + | ===Untersuchungsergebnisse=== | ||
| + | |||
| + | [[File:AdaptiveTragwerke7.png|right|thumb|450px|Übersicht Berechnungsergebnisse <ref name = "Q10"></ref>]] | ||
| + | Die Parameteruntersuchung hat gezeigt, dass durch die Verwendung von Federn die Steifigkeit des Gesamtsystems verändert werden kann. Dadurch können die vorhandenen Tragreserven von statisch unbestimmten Systemen genutzt werden. Auch die Werte in der nebenstehenden Abbildung spiegeln die Ergebnisse wider. Durch den '''Einsatz von Federn''' können sowohl die '''Durchbiegung''' als auch die auftretenden '''Momente''' des betrachteten Systems deutlich reduziert werden. Die Untersuchung ist hier als eine exemplarische Grundlage anzusehen und muss im Einzelfall immer genauer betrachtet werden. Es handelt sich hierbei lediglich um überschlägliche Tendenzen. Solche Systeme müssen zur praktischen Umsetzung immer im Einzelfall betrachtet und untersucht werden. Für die Umsetzung fehlt es zum einen an Sicherheitskonzepten bzw. Normen und zum anderen sollten hierfür die einzelnen Parameter sowohl eindeutig festgelegt werden als auch deutlich genauer analysiert und betrachtet werden. Die zu wählende Federsteifigkeit bzw. die notwendige Bandbreite an Federsteifigkeiten zur Adaption ist immer von dem konkreten Bauwerk und dessen Geometrie, Belastung und Steifigkeit abhängig. | ||
| + | Durch die Erhöhung der Anzahl an Federn, kann das System zielgerichteter optimiert werden, jedoch wird hier der Rechenaufwand deutlich komplizierter und umfangreicher. Die Umsetzung kann dann nur noch softwareunterstützt durchgeführt werden. Außerdem sollte hier auch über eine softwaregestützte und umfangreiche Finite-Elemente-Methode nachgedacht werden, um die Anzahl der zu berechnenden Knoten bzw. Stellen des | ||
| + | Systems breiter aufzustellen und so die Genauigkeit der Ergebnisse zu erhöhen. Auch die Dimensionierung und bauliche Umsetzung solcher Systeme <br /> | ||
| + | spielt hierbei eine große Rolle.<ref name = "Q10"></ref> | ||
| + | |||
| + | =Einsatz Elektromagnet= | ||
| + | |||
| + | [[File:AdaptiveTragwerke8.png|right|thumb|350px|Skizze Positionierung Elektromagnet <ref name = "Q10"></ref> ]] | ||
| + | Die Master-Thesis <ref name = "Q10"></ref> zeigt '''weiteren Forschungsbedarf''' hinsichtlich adaptiver Systeme auf. Das Gebiet der adaptiven Systemen im Bauwesen bietet noch ein weites Feld für mögliche Forschungsarbeiten, um sowohl die Umsetzung adaptiver Tragwerke mithilfe einer Steifigkeitsadaption zu untersuchen als auch grundlegende rechnerische Ansätze zu definieren. In besonderer Weise könnte man sich hier auf die baupraktische Umsetzung mittels Elektromagneten und/oder elektrorheologische Fluide als Aktuatoren in einem adaptiven System konzentrieren, da hierzu noch keine vorhandenen Forschungsergebnisse vorliegen. Sowohl die Elektromagnete als auch die eingesetzten Fluide müssten dabei steuerbar und ausreichend sicher und stabil umgesetzt werden. Hierzu müssten deutlich genauere und umfangreiche Berechnungen durchgeführt werden. Modelle (ähnlich wie bei dem Stuttgarter Träger) können hierbei zu einer Simulation einer praktischen Umsetzung dienen. Des Weiteren wäre eine Erstellung normgerechter Entwurfskonzepte und Sicherheitsanforderungen für adaptive Tragwerke denkbar. | ||
| + | |||
| + | <br /> | ||
=Quellen= | =Quellen= | ||
| Zeile 60: | Zeile 199: | ||
{{Seiteninfo | {{Seiteninfo | ||
| − | |Quality-flag = [[File:quality-flag- | + | |Quality-flag = [[File:quality-flag-white.gif|right|70px]] |
| − | |Status = Seite in Bearbeitung | + | |Status = Seite in Bearbeitung|}} |
| + | [[Kategorie:Grundlagen/Begriffe-Baustatik]] | ||
[[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
| + | [[Kategorie:Grundlagen/Begriffe-Stahlbau]] | ||
Aktuelle Version vom 28. März 2023, 11:58 Uhr
Als adaptive Tragwerke (von lateinisch adaptare "anpassen") bezeichnet man Systeme, die in der Lage sind, sich ihrer Umgebung und den äußeren Einflüssen anzupassen und auf diese angemessen zu reagieren. Es entsteht in gewisser Weise ein Wechselspiel zwischen der Umgebung und dem Tragwerk selbst, welches zu einer Optimierung von vorher festgelegten Eigenschaften und Zielen führt. Ziel solcher Tragwerksentwürfe ist es, dass das System mittels aktiver Elemente in der Lage ist, auf unterschiedliche Situationen und Lastfälle zu reagieren und sich anzupassen. Durch die Integration aktiver Elemente können in der Bemessung auftretende Steifigkeitsprobleme in Festigkeitsprobleme überführt werden. Hier ergibt sich ein entscheidender Vorteil hinsichtlich Masseneinsparung, sodass Überdimensionierungen verhindern werden können.
Der Ursprung solcher Systeme ist auf die Natur zurückzuführen. Chamäleons sind in der Lage, sich farblich ihrer Umgebung anzupassen, um sich vor Feinden zu schützen. Dieses Prinzip der Anpassung kann auch die Technik übertragen werden. Bereits in der Luft- und Raumfahrt Technik, in der Automobilbranche und auch in der Optik lassen sich unterschiedliche adaptive Systeme wiederfinden (automatisch einfahrbare Tragflächen Flugzeug, adaptive Fahrwerke, adaptive Optik).
Die Idee adaptiver Tragwerke im Bauwesen besteht darin, Material einzusparen und durch externe Energie zu "ersetzen".
Allgemein werden adaptive Systeme unterschieden in: aktiv und passiv. Teilweise wird in der Wissenschaft auch von Hybridsystemen gesprochen.
Ziele und Gründe für Adaption
Mit Blick auf die aktuellen sozialen Probleme wie die Entwicklung der wachsenden Weltbevölkerung, der herrschender Materialknappheit und dem Klimawandel ist ein Umbruch vor allem in der Baubranche zwingend notwendig. Die Baubranche macht derzeit mehr als 50% der globalen Ressourcennutzung und rund 1/3 der globalen CO2 Emissionen aus. Ressourcenschonendes und wirtschaftliches Entwerfen und Konstruieren von Bauwerken waren schon immer ein Bestreben im Ingenieurwesen gewesen und gewinnen aktuell und in Zukunft noch mehr an Bedeutung. Dafür sind neue Entwurfsansätze zwingend notwendig.
Mittels adaptiver Tragwerke können folgende Optimierungsziele verfolgt werden: [1]:
- Verringerung von Verformungen
- Höhere Tragfähigkeiten
- Optimierung des Schwingungsverhalten
- Reduzierung des Ressourcen- und Energieverbrauchs
- Größere Spannweiten und höhere Konstruktionen
- Mehr Komfort bei der Nutzung (bezogen auf die Raumqualität und Adaption von Fassaden)
- Verlängerung der Lebensdauer
Systemübersicht und Elemente
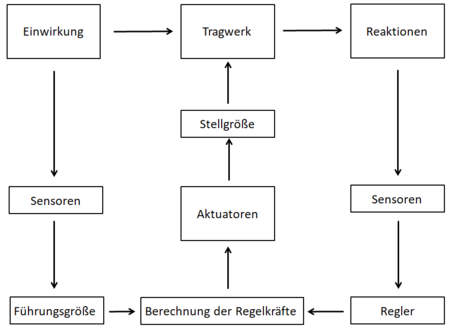
Durch das Integrieren von multifunktionalen Bauteilen entstehen intelligente und dadurch anpassungsfähige Systeme. Infolge der Anpassungsfähigkeit,
können diese Systeme (oder übertragen auf das Bauwesen Tragwerke) auf unterschiedlichste Einwirkungen reagieren.
Solche Systeme bestehen allgemein aus den folgenden drei Komponenten:
- Sensoren: zur kontinuierlichen Messung äußerer Einflüsse oder systeminterner Zustände (z.B. Dehnungsmessstreifen usw.)
- Steuerung und Regelung: Verarbeitung der von den Sensoren gemessenen Information und Weitergabe an Aktuatoren
- Aktuatoren: Ausführungselement der notwendigen Adaption (z.B. Hydraulikzylinder)
Sensoren
Den Sensoren ist die Aufgabe der Übertragung von Informationen zuzuordnen. Sie sind in der Lage, Veränderungen der Systemeinflüsse wahrzunehmen und den internen Zustand des Systems kontinuierlich zu messen.[3] Ein Sensor ist somit das erste Element in der Reihenfolge adaptiver Systeme. Im Allgemeinen erzeugen die Sensoren ein elektrisches Ausgangssignal, welches an die Steuerung bzw. Regelung weitergegeben wird. Dort wird es verarbeitet, umgewandelt und dann an die Aktuatoren des Systems weitergeleitet. [4]
Zu den an den häufigsten verwendeten Sensoren gehören die Dehnungsmessstreifen (kurz DMS), welche zur Messung von Dehnungen geeignet sind und somit ein typisches Beispiel der “Wegmessung“ darstellen.
Steuerung und Regelung
Bei adaptiven Systemen wird in Steuerung und Regelung differenziert. Der Unterschied bei der Anwendungen liegt darin, dass bei einer Steuerung lediglich die äußeren Einflüsse ermittelt werden, während bei der Regelung Systemantworten generiert werden. Dementsprechend spricht man bei der Abhängigkeit zur Optimierung durch äußere Lasten von Steuerung und bei Systemverformungen oder der Variation der Systemeigenschaften von Regelung. Das bedeutet, dass eine Regelung zur Ausführung der Adaption innerhalb eines Systems unabdingbar ist.[1]
Aktuatoren
Die Aktuatoren oder Aktoren in einem System lassen sich auch als “Stellgrößen“ bezeichnen. Sie sind dafür zuständig, die von der Steuerung bzw. Regelung übertragenden Signale und Informationen umzusetzen und somit die Adaption auszuführen. Sie bilden daher das Gegenstück bzw. Bindeglied zu den Sensoren.
Die Aktuatoren eines Systems transformieren dabei elektrische Signale in mechanische oder chemische Größen.[3] Für die Umsetzung dieser technischen Prozesse ist meistens eine elektrische, hydraulische oder pneumatische Hilfsenergie erforderlich. Da Aktuatoren keine dauerhafte Arbeit leisten müssen, sondern nur kurzfristig zum Einsatz kommen, müssen diese Elemente bestimmte Anforderungen erfüllen [4]:
- Möglichst lineare bzw. statische Übertragungseigenschaften
- Funktionen Antreiben und Bremsen
- Hohe Belastbarkeit
- Möglichkeit zur genauen Positionierung
- Schnelle, gut gedämpfte dynamische Eigenschaften
- Geeignete Schnittstellen für Sensoren
Im Allgemeinen können Aktuatoren für verschiedene Aufgaben eingesetzt werden. Die Aktuatoren werden dabei in Kategorien nach dem jeweiligen technischen Prozess bzw. nach den notwendigen Hilfsenergien unterteilt.
Passive Systeme
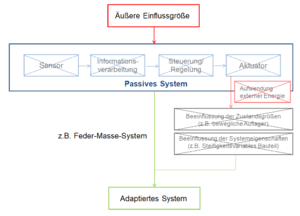
Bei der passiven Adaption reagieren die Systeme direkt auf die Einflüsse ohne jeglichen Einsatz von Steuerung durch zum Beispiel Sensoren.
Somit ist eine Zuwendung externer Energie nicht notwendig. Bei passiven Systemen wird die Bewegung und Dynamik des Tragwerkes selbst genutzt und die dadurch entstandene Energie absorbiert.[6]
Typische Beispiele passiver Adaption sind Feder-Masse-Systeme, die als Schwingungstilger oder –Dämpfer, die auf das Tragwerk einwirkende Energie aufnehmen und diese in eine Relativbewegung
zur Absorption umwandeln können. Denkbar sind auch Systeme, die frei drehbar sind und sich beispielsweise der jeweiligen Windrichtung anpassen können.
Aktive Systeme
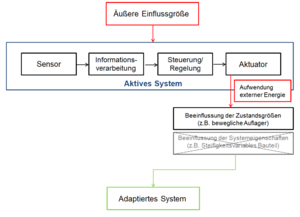
Im Gegensatz zur passiven Adaption ist bei einer aktiven Adaption das Aufbringen externer Energie zur Aktivierung der Steuerung notwendig.
Die Aktivierung wird durch zusätzliche Sensoren ausgelöst, gesteuert und durch die integrierten Aktuatoren umgesetzt. Häufig kommen an dieser Stelle elektrohydraulische oder elektromechanische Aktuatoren zum Einsatz.[6] Ein Vorteil der aktiven Adaption mit dieser Steuerung ist eine größere Abdeckung der Anpassungsfähigkeit der Systeme. Die Reaktionen und möglichen Steuerungen dieser Systeme sind deutlich weitreichender. Aktive Systeme werden häufig dazu eingesetzt, um die jeweiligen Zustandsgrößen (Verformungen und innere Kräfte) zu beeinflussen.[5]
Semi-aktive Systeme
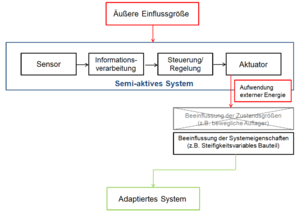
Semi-aktive Systeme sind eine Kombination aus aktiven und passiven Systemen, bei denen die Vorteile beider Systeme kombiniert genutzt werden.[1] Bei diesen Systemen wird die Adaption durch eine Manipulation der jeweiligen Systemeigenschaft (z.B. der Steifigkeit oder durch Dämpfung) hervorgerufen. Semi-aktive Systeme sind auch auf eine externe Energiequelle angewiesen. Allerdings ist die notwendige Hilfsenergie deutlich geringer als bei aktiven Systemen, dabei wird die Anpassungsfähigkeit jedoch nicht beeinträchtigt.[1] Semi-aktive Regelsysteme werden vor allem zur Nutzung von Steifigkeitsregelungsgeräten, elektrorheologischen und magnetorheologischen Dämpfern oder abgestimmten Flüssigkeitsdämpfern erforscht.[6]
Anwendung im Bauwesen
Voraussetzungen
Adaptive Tragwerke kommen teilweise im Bauwesen bereits zur Anwendung (z.B. zur Schwingungstilgung oder in Fassaden). Dabei müssen die Systeme einige Grundvoraussetzungen erfüllen. Die wichtigste Grundvoraussetzung zur Optimierung von Tragwerken sind veränderbare Systemgrößen. Wenn das zu optimierende System keine Veränderungen zulässt, ist eine mögliche Adaption ausgeschlossen. Veränderliche Systemgrößen können dabei zum Beispiel sein:
- Systemkräfte und Lasteinleitung, welche sowohl Schnittgrößen als auch Verformungen beeinflussen können.
- Die Geometrie und maßgebende Formgebung des Tragwerks können bei der Aufnahme von Lasten eine entscheidende Stellgröße darstellen.
- Unterschiedliche Steifigkeiten von Einzelelementen oder auch von Bereichen innerhalb des Systems können ebenfalls zu einer Reduzierung der Schnittkräfte führen. Durch Steifigkeiten können somit bestimmte veränderliche Einwirkungen homogenisiert werden.[1]
- Ähnlich wie die Steifigkeit kann auch die Masse eines Systems eine entscheidende Rolle zur Adaption der Tragwerke besitzen und zur Lastaufnahme beitragen.
Somit können unterschiedliche Größen eines Systems optimiert und verschiedene Einflüsse adaptiert werden. Dabei wird die Adaption unterschieden in Verformungsadaption und Schnittgrößenadaption.
Verformungsadaption
Bei der Verformungsadaption sollen ermittelte Verformungen oder Verschiebungen optimiert werden. Dazu müssen zunächst die erforderlichen Dehnungen, Längenänderungen und Arbeiten der einzelnen Elemente ermittelt werden. Nachfolgend können die Kräfte zur Verhinderung dieser Verschiebungen ermittelt werden. Diese müssen dann für die Adaption entgegenwirken, um die Verformungen somit zu homogenisieren. Teilweise können auch Verformungen eines Systems zur Optimierung vorgegeben werden (z.B. Überhöhung bei Brücken). (Beispiel: Stuttgarter Träger)
Schnittgrößenadaption
Schnittgrößen- oder auch Momentenadaption genannt, hat zum Ziel die Schnittgrößen eines Systems durch z.B. Änderung der Steifigkeit oder Lasteinleitung zu homogenisieren. Auch die Formgebung des Gesamtsystems kann sich positiv auf die Schnittgrößen auswirken, z.B. kann die Struktur dem Momentenverlauf angepasst werden. Oftmals wird die Angleichung der Feld- und Stützmomente zum Optimierungsziel gewählt. Typische Anwendungen in der Baupraxis sind auch Systeme zur Dämpfung von dynamischen Lasten wie Schwingungen oder Erdbeben. (Beispiel: Thyssenkrupp Elevator Testturm)
Steifigkeitsadaption
Die Steifigkeitsadaption gehört auch zu der Schnittgrößenadaption. Häufig wird bei der Schnittgrößenadaption jedoch auf die Formgebung des Tragwerks zur optimalen Lastaufnahme oder einer Schwingungsdämpfung gesprochen. Bei der Steifigkeitsadaption allerdings sollen das Tragwerk oder nur einzelne Bauteile in der Lage sein, ihre Steifigkeiten zu ändern, um somit beispielswiese innere Lasten oder auch Verformungen zu verringern. Durch die interne Änderung der Steifigkeiten können gewisse Beanspruchungszustände homogenisiert werden.[7] “The Kajima Technical Research Institute“ wurde 1990 erbaut und ist das erste Gebäude mit veränderbaren Steifigkeiten. Bei diesem Gebäude können aus Erdbeben entstehende Horizontallasten optimal übertragen werden. Die Adaption erfolgt durch den Einsatz eines hydraulischen Systems, mit dem die Steifigkeit des Tragwerkes beeinflusst werden kann. Je nach Steifigkeit dieser Elemente variiert das statische System zwischen einem Fachwerk (steif) und einem Rahmen (weich) [8], wodurch die Lastverteilung variiert werden kann.
Wie bereits erwähnt ist vor allem der Einsatz von semi-aktiven Regelsystemen zur Steifigkeitsadaption z.B. in Form von Steifigkeitsregelgeräten denkbar. Dabei dienen regelbare Steifigkeitsvorrichtungen der Aussteifung eines Systems bzw. Gebäudes vor allem unter Lasten, die durch Erdbeben entstehen. Ähnlich wie bei dem oben erwähnten Technical Research Institute werden dabei die Steifigkeitsvorrichtungen je Stockwerk eingeklinkt oder freigegeben. Es handelt sich dabei um einen Hydraulikzylinder (doppeltwirkende Kolbenstange) mit einem Magnetventil. Das Magnetventil verbindet die beiden Kammern und steuert somit den Flüssigkeitsstrom zum Aktivieren bzw. Deaktivieren der Aussteifung. Der Betrieb braucht in etwa eine Leistung von 20 W und eine Zeit von 30 ms.[9]
Einflüsse auf die Adaption eines Tragwerkes
Um Adaptionsvorgänge von Systemen zu analysieren, muss die Varianz der Geometrie und das Tragverhalten des unbelasteten Tragwerks untersucht werden. Weiterhin müssen auch Betrachtungen aus Theorie 2. Ordnung hinzugezogen werden, da die Dehnungen und Stellwege der Aktuatoren einen großen Einfluss auf die Tragwerksverformungen haben können. Da während der Adaption einzelne Parameter oder teilweise die gesamte Geometrie des Grundsystems verändert werden, sind die einzelnen Systeme nicht konstant und werden de facto immer wieder neu definiert.[1] Im Wesentlichen wird der Optimierungsprozess sowohl durch den Zeitpunkt der Lastaufbringung als auch durch auftretende Tragwerksverformungen beeinflusst. Aber auch Faktoren wie die notwendige Adaptionsarbeit und einzuhaltende Sicherheitsanforderungen (Tragfähigkeit und Gebrauchstauglichkeit) sind dabei nicht zu vernachlässigen. Sie nehmen dabei einen wesentlichen Einfluss auf den Entwurf und die Berechnung adaptiver Tragwerke. Dazu muss vor allem die Einflussnahme der Geometrieänderungen des unbelasteten Tragwerkes untersucht werden.
Adaptionsarbeit
Die Adaptionsarbeit bezeichnet den Aufwand, der zum Erreichen der Adaption notwendig ist. Die Adaptionsarbeit setzt sich zum einen aus der Arbeit der adaptierenden Kräfte als auch zum anderen aus dem Betrag des inneren Potentials des Tragwerks zusammen. Das innere Potential beschreibt dabei die Änderungen innerhalb des Systems während des Adaptionsprozesses. Dabei wird die Formänderungsarbeit innerhalb des Tragwerkes als Energie gespeichert und bei Entlastung wieder freigegeben. Durch die Adaption wird dieses Energiepotenzial der inneren Kräfte um den Betrag verändert.[1]
Für die Ermittlung der Adaptionsarbeit sind neben den geometrischen Veränderungen und dem Zeitpunkt der Adaption weiterhin zwei Fallunterscheidungen zu betrachten:
- Störungsfreier Betrieb und
- Versagensfall
Einfluss des Zeitpunktes der Adaption
Der Zeitpunkt der Lastaufbringung hat für die Adaption selbst und für die aufzubringende Adaptionsarbeit einen entscheidenden Einfluss. Dabei werden in der Theorie die folgenden drei Grenzfälle unterschieden:
Adaption vor der Lastaufbringung:
Das Adaptionsziel wird erst nach der Lastaufbringung erreicht, da die Geometrie im Vorfeld durch z.B. Vorspannungen (Schnittgrößenadaption) oder eine Überhöhung (Verformungsadaption) optimiert bzw. beeinflusst wird. Die erforderliche Adaptionsarbeit ist für diesen Grenzfall am kleinsten.
Adaption nach der Lastaufbringung:
Die Adaption findet erst nach der Lastaufbringung statt, sodass entgegen der Last gearbeitet werden muss. In diesem Fall ist die notwendige Adaptionsarbeit maximal.
Adaption während der Lastaufbringung:
In diesem Grenzfall erfolgt die Adaption des Tragwerkes nach Möglichkeit zeitgleich mit der Lastaufbringung. Diese Betrachtung stellt in der Praxis auch den Regelfall dar. Die erforderliche Adaptionsarbeit pendelt sich dabei zwischen den beiden zuvor genannten Grenzfällen ein.[1]
Einfluss der Tragsicherheit und Gebrauchstauglichkeit
Da Tragwerke in der Regel darauf ausgelegt sind, bestimmte Verformungen aufnehmen zu können, ohne zu versagen, ist eine vollständige Adaption der Verformungen auf null nicht immer sinnvoll. Außerdem müssen auch die Zusammenhänge der Schnittgrößen in den unterschiedlichen Zuständen eines Systems (passiv, aktiv und adaptiert) berücksichtigt werden.
Das Sicherheitskonzept adaptiver Tragwerke ist von großer Bedeutung, da es bei solchen Systemen zum Einsatz technischer Komponenten kommt. Es muss immer sichergestellt werden, dass das adaptive Tragwerk auch beim Ausfall der adaptiven Elemente nicht versagt. Die Gebrauchstauglichkeit kann dabei zunächst vernachlässigt werden. In Anlehnung an die bereits bekannten Sicherheitskonzepte aus dem Eurocode 0 zur Berechnung von Tragwerken, gibt es für den Entwurf von adaptiven Tragwerken unterschiedliche Herangehensweisen.[1]
Systemoptimierung
Im Wesentlichen ist die Optimierung eines Systems hauptsächlich von den Auflagerbedingungen (Anzahl, Ort und Art der Auflager) und einer optimalen Stützweite abhängig. Dabei bestimmt die Anzahl der Auflager den Grad der statischen Unbestimmtheit. Die Anzahl und auch die Position der Auflager nehmen dabei einen entscheidenden Einfluss auf die Größen der Momente. Durch eine sinnvolle Anordnung kann ein ausgeglichener Momentverlauf mit in etwa gleich großen Maximal- und Minimalwerten erreicht werden. Allgemein sollten die folgenden Anforderungen bei der Optimierung des Systems beachtet werden:
- Gleichmäßige Verteilung der Lasten, gegebenenfalls System von Beginn an optimieren hinsichtlich der Lasteinleitung und -verteilung
- Große Stützweiten vermeiden
- Statisch unbestimmte Systeme haben deutlich mehr Tragkapazitäten
- Die Anzahl der Auflager bzw. Federn können den Momentenverlauf maßgebend beeinflussen
Möglichkeiten der Steifigkeitsadaption
Bei dem bereits aufgeführten Beispiel “The Kajima Technical Research Institute“ findet die Steifigkeitsadaption Anwendung, indem phasen- bzw. steifigkeitsverändernde Bauteile dazu genutzt werden, die Art des statischen Systems zu beeinflussen. Im Rahmen einer Master-Thesis mit dem Titel "Möglichkeiten der Steifigkeitsadaption bei statisch unbestimmten Trägersystemen" [10] wurden erste Berechnungsansätze zur Steifigkeitsadaption anhand von federgelagerten Systemen durchgeführt und untersucht. Federlagerungen werden im Bauwesen allgemein durch elastische Auflager oder Anschlüsse praktisch umgesetzt. Fundamente werden auch häufig als federgelagertes Systeme angesetzt, da so für den anstehenden Boden bzw. die Bettung eine gewisse Nachgiebigkeit berücksichtig werden kann. Solche Systeme haben aber nur begrenzte Kapazitäten und basieren auf zuvor getroffenen Annahmen. Dabei sind dann die Auflager oder auch der Boden nicht regelbar und in der Lage, gesteuert zu werden. Bei der Adaption ist eine aktive Steuerung bzw. Regelung einzelner Elemente zur Abdeckung größerer Optimierungsspektren durch zum Beispiel semi-aktive Systeme denkbar. Die Aktuatoren (Federn) können aktiv gesteuert werden, um so auf die äußeren Einflüsse reagieren zu können und bessere Systemeigenschaften hervorzurufen. Dazu müssen ständige Messungen der momentanen Belastungen durchgeführt werden, um die Steifigkeiten der Federn in Abhängigkeit dazu zu justieren. Hierbei sind Sensoren wie Dehnungsmessstreifen (DMS) oder Kraftmesser denkbar. Aus der Summe der gemessenen Kräfte jedes Auflagers ergibt sich die Gesamtbelastung. Aus den Differenzen kann der Ort der Belastung ermittelt werden. Die ermittelten Kräfte können dann über die Sensoren an die Regeleinheit des Systems weitergegeben werden. Diese sendet dann die Information durch Signale an die Aktuatoren, welche die jeweils notwendige Adaption der Steifigkeiten durchführt.
Berechnungsansätze
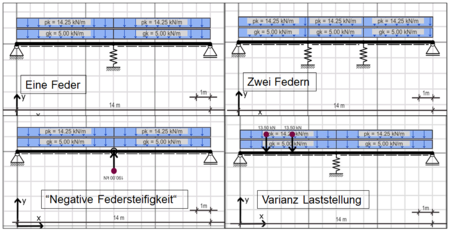
In der erwähnten Master-Thesis [10] wurden verschiedene Zusammenhänge der Steifigkeitsadaption unter der Verwendung von Federn durch eine Parameteruntersuchung herausgearbeitet. Je steifer die Feder eingestellt wird, desto “anziehender“ wirkt diese auf die einwirkenden Kräfte und fungiert wie ein festes Auflager. Bei weicheren Federn können dementsprechend weniger Kräfte aufgenommen werden und auch die Verformungen sind an dieser Stelle größer. Um die jeweiligen Einflüsse der unterschiedlichen Stellgrößen innerhalb eines Systems zu untersuchen und zu beurteilen, wurden die Parameter isoliert voneinander betrachtet. Dabei wurden unterschiedliche Systeme untersucht. Die nebenstehende Abbildung zeigt den grundsätzlichen Aufbau des untersuchten Systems. Es wurden sowohl zwei-Feld-Träger mit einer Feder als als auch drei-Feld-Träger mit zwei Federn untersucht, bei denen die Federn jeweils in ihrer Federsteifigkeit kF variiert wurden. Weiterhin wurde der Sonderfall einer "negativen" Federsteifigkeit durch eine nach oben gerichtete Kraft simuliert. Auch die Varianz der Laststellungen wurden im Anschluss daran betrachtet.
Untersuchungsergebnisse
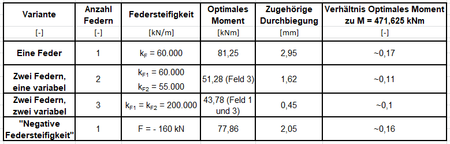
Die Parameteruntersuchung hat gezeigt, dass durch die Verwendung von Federn die Steifigkeit des Gesamtsystems verändert werden kann. Dadurch können die vorhandenen Tragreserven von statisch unbestimmten Systemen genutzt werden. Auch die Werte in der nebenstehenden Abbildung spiegeln die Ergebnisse wider. Durch den Einsatz von Federn können sowohl die Durchbiegung als auch die auftretenden Momente des betrachteten Systems deutlich reduziert werden. Die Untersuchung ist hier als eine exemplarische Grundlage anzusehen und muss im Einzelfall immer genauer betrachtet werden. Es handelt sich hierbei lediglich um überschlägliche Tendenzen. Solche Systeme müssen zur praktischen Umsetzung immer im Einzelfall betrachtet und untersucht werden. Für die Umsetzung fehlt es zum einen an Sicherheitskonzepten bzw. Normen und zum anderen sollten hierfür die einzelnen Parameter sowohl eindeutig festgelegt werden als auch deutlich genauer analysiert und betrachtet werden. Die zu wählende Federsteifigkeit bzw. die notwendige Bandbreite an Federsteifigkeiten zur Adaption ist immer von dem konkreten Bauwerk und dessen Geometrie, Belastung und Steifigkeit abhängig.
Durch die Erhöhung der Anzahl an Federn, kann das System zielgerichteter optimiert werden, jedoch wird hier der Rechenaufwand deutlich komplizierter und umfangreicher. Die Umsetzung kann dann nur noch softwareunterstützt durchgeführt werden. Außerdem sollte hier auch über eine softwaregestützte und umfangreiche Finite-Elemente-Methode nachgedacht werden, um die Anzahl der zu berechnenden Knoten bzw. Stellen des
Systems breiter aufzustellen und so die Genauigkeit der Ergebnisse zu erhöhen. Auch die Dimensionierung und bauliche Umsetzung solcher Systeme
spielt hierbei eine große Rolle.[10]
Einsatz Elektromagnet
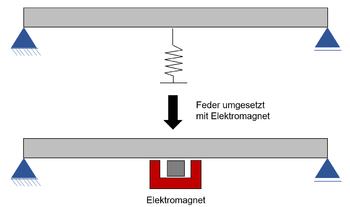
Die Master-Thesis [10] zeigt weiteren Forschungsbedarf hinsichtlich adaptiver Systeme auf. Das Gebiet der adaptiven Systemen im Bauwesen bietet noch ein weites Feld für mögliche Forschungsarbeiten, um sowohl die Umsetzung adaptiver Tragwerke mithilfe einer Steifigkeitsadaption zu untersuchen als auch grundlegende rechnerische Ansätze zu definieren. In besonderer Weise könnte man sich hier auf die baupraktische Umsetzung mittels Elektromagneten und/oder elektrorheologische Fluide als Aktuatoren in einem adaptiven System konzentrieren, da hierzu noch keine vorhandenen Forschungsergebnisse vorliegen. Sowohl die Elektromagnete als auch die eingesetzten Fluide müssten dabei steuerbar und ausreichend sicher und stabil umgesetzt werden. Hierzu müssten deutlich genauere und umfangreiche Berechnungen durchgeführt werden. Modelle (ähnlich wie bei dem Stuttgarter Träger) können hierbei zu einer Simulation einer praktischen Umsetzung dienen. Des Weiteren wäre eine Erstellung normgerechter Entwurfskonzepte und Sicherheitsanforderungen für adaptive Tragwerke denkbar.
Quellen
- ↑ 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 Pawlowski, Robert: Adaptive Dachtragwerke – Entwicklung eines Entwurfsverfahrens – Betrachtung ausgewählter Aspekte. Dissertation: Technische Universität München, 2006
- ↑ Weber, Christian-Toralf: Ein Beitrag zur optimalen Positionierung von Aktoren in adaptiven mechanischen Strukturen, Düsseldorf: VDI, 1998
- ↑ 3,0 3,1 Teuffel, Patrick: Entwerfen adaptiver Strukturen, Lastpfadmanagement zur Optimierung tragender Leichtbaukonstruktionen. Dissertation: Universität Stuttgart, 2004
- ↑ 4,0 4,1 Isermann, Rolf: Mechatronische Systeme: Grundlagen, Berlin, Heidelberg, New York: Springer-Verlag, 1999
- ↑ 5,0 5,1 5,2 5,3 Bretz, A.; Calmano, S. et al.: Darstellung passive, semi-aktiver und aktiver Systeme auf Basis eines Prozessmodells, SFB 805, TU Darmstadt
- ↑ 6,0 6,1 6,2 Symans, M. D.; et al.: Semi-active control systems for seismic protection of structures: a state-of-the-art review. In: Engineering structures 21, Seiten 469-487
- ↑ Sobek, Werner; Haase, Walter, et al.: Adaptive Systeme. In: Stahlbau 7/69, Berlin: Ernst & Sohn, 2000
- ↑ Culshaw, Brian: Smart Structures and Materials, Boston, London: Artech House, 1996
- ↑ Kobori T.; Takahashi M. et al.: Seismic response controlled structure with active variable stiffness system. In: Earthquake Engineering and Structural Dynamics, 1993
- ↑ 10,0 10,1 10,2 10,3 10,4 10,5 10,6 Schwegmann, Lisa: Möglichkeiten der Steifigkeitsadaption bei statisch unbestimmten Trägersystemen, Master-Thesis: Hochschule Wismar, 2021
Seiteninfo
|
