Randstreifenfundament nach Kanya: Unterschied zwischen den Versionen
Gbolle (Diskussion | Beiträge) K (→Formeln) |
|||
| (42 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | [[Datei:Bemessung_eines_Randstreifenfundaments_(Bsp.)_8.JPG|mini|Momente am biegesteifen Anschluss]] | |
| − | |||
| − | |||
Das Berechnungsverfahren nach Josef Kanya beschäftigt sich mit dem | Das Berechnungsverfahren nach Josef Kanya beschäftigt sich mit dem | ||
Spezialfall des exzentrisch belasteten Streifenfundaments. In der Baupraxis | Spezialfall des exzentrisch belasteten Streifenfundaments. In der Baupraxis | ||
| Zeile 15: | Zeile 13: | ||
angeschlossenen Platten und Wänden (auch Zentrierplatte bzw. | angeschlossenen Platten und Wänden (auch Zentrierplatte bzw. | ||
Zentriermoment genannt) berücksichtigen. Dadurch werden der Wert der Exzentrizität stark verbessert und schädliche | Zentriermoment genannt) berücksichtigen. Dadurch werden der Wert der Exzentrizität stark verbessert und schädliche | ||
| − | Verformungen verhindert. Kanya<ref>J. Kanya, „Berechnung ausmittig belasteter Streifenfundamente mit Zentrierung durch eine Stahlbeton-Fußbodenplatte,“ Die Bautechnik, pp. 154-159, Mai 1969</ref> hat diese Methoden aufgegriffen und auf dieser Grundlage Berechnungsformeln entwickelt, die auch die vorher nicht | + | Verformungen verhindert. Kanya<ref name="Kanya">J. Kanya, „Berechnung ausmittig belasteter Streifenfundamente mit Zentrierung durch eine Stahlbeton-Fußbodenplatte,“ Die Bautechnik, pp. 154-159, Mai 1969</ref> hat diese Methoden aufgegriffen und auf dieser Grundlage Berechnungsformeln entwickelt, die auch die vorher nicht |
berücksichtigte Zentrierzugkraft und die Verschiebung des | berücksichtigte Zentrierzugkraft und die Verschiebung des | ||
Fundamentschwerpunktes beinhalten. | Fundamentschwerpunktes beinhalten. | ||
| Zeile 37: | Zeile 35: | ||
==Formelzeichen== | ==Formelzeichen== | ||
| − | [[Datei:Randstreifenfundament_nach_Kanya_1.JPG| | + | [[Datei:Randstreifenfundament_nach_Kanya_1.JPG|600px|thumb|right|Gesamtübersicht Kanya-Verfahren]] |
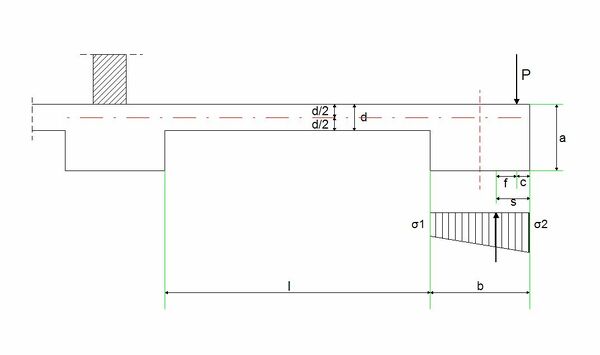
| − | Für das bessere Verständnis der Berechnungsformeln folgt eine Tabelle mit der Auflistung aller verwendeten Formelzeichen in den Gleichungen. | + | Für das bessere Verständnis der Berechnungsformeln folgt eine Tabelle mit der Auflistung aller verwendeten Formelzeichen in den Gleichungen. |
{| class="wikitable" | {| class="wikitable" | ||
!Formelzeichen!!Einheit!!Beschreibung | !Formelzeichen!!Einheit!!Beschreibung | ||
|- | |- | ||
|E<sub>B</sub>||kN/cm<sup>2</sup>||Elastizitätsmodul des Stahlbetons | |E<sub>B</sub>||kN/cm<sup>2</sup>||Elastizitätsmodul des Stahlbetons | ||
| + | |- | ||
| + | |F<sub>B</sub>||cm<sup>2</sup>||Querschnittsfläche 1 cm breiter Zentrierplatte | ||
| + | |- | ||
| + | |I<sub>B</sub>||cm<sup>4</sup>||Trägheitsmoment 1 cm breiter Zentrierplatte | ||
| + | |- | ||
| + | |E<sub>s</sub>||kN/cm<sup>2</sup>||Steifemodul des Bodens | ||
| + | |- | ||
| + | |a||cm||Höhe des Randfundaments | ||
| + | |- | ||
| + | |b||cm||Breite des Randfundaments | ||
| + | |- | ||
| + | |c||cm||Randabstand der Last P | ||
| + | |- | ||
| + | |d||cm||Dicke der Zentrierplatte | ||
| + | |- | ||
| + | |l||cm||lichte Spannweite der Zentrierplatte | ||
| + | |- | ||
| + | |P||kN/cm||Belastung pro lfd. cm | ||
| + | |- | ||
| + | |M<sub>1</sub>||kNcm/cm||Moment in der Sohlfuge durch H<sub>Z</sub> | ||
| + | |- | ||
| + | |H<sub>B</sub>||kN/cm||Reibungskraft in der Sohlfuge pro lfd. cm | ||
| + | |- | ||
| + | |σ<sub>1</sub>||kN/cm<sub>2</sub>||Sohlspannung Innenkante Randfundament | ||
| + | |- | ||
| + | |σ<sub>2</sub>||kN/cm<sub>2</sub>||Sohlspannung Außenkante Randfundament | ||
| + | |- | ||
| + | |M<sub>Z</sub>||kNcm/cm||Zentriermoment pro lfd. cm | ||
| + | |- | ||
| + | |H<sub>Z</sub>||kN/cm||Zentrierzugkraft pro lfd. cm | ||
|} | |} | ||
<br /> | <br /> | ||
| + | ==Formeln== | ||
| + | Zur Lösung werden die Gleichungen der Kräftesummen in der Sohlfuge aufgestellt. | ||
| + | <br /> | ||
| + | ;Grundbedingungen | ||
| + | <br /> | ||
| + | :<math>\sum M=0 \to P \cdot f-M_{1}-M_{z}=0</math> | ||
| + | :<math>\sum H=0 \to H_{B} - H_{Z}=0</math> | ||
| + | :<math>\sum V=0 \to P = | ||
| + | \frac{\sigma_{1}+\sigma_{2}}{2} \cdot b</math> | ||
| + | |||
| + | <br /> | ||
| + | Durch Umformung und Einsetzen der Größen aus der vorherigen Tabelle erhält man die Gleichung für σ<sub>2</sub>. | ||
| + | <br /> | ||
| + | :<math> | ||
| + | \sigma_{2} = | ||
| + | \frac | ||
| + | {\frac{2}{3} \cdot b^{2} - c \cdot b + \frac{2 \cdot \left( a - \frac{d}{2} \right) ^{2}}{3 F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B} + 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}}} | ||
| + | {\frac{b^{2}}{6} + \frac{2 \cdot \left( a - \frac{d}{2} \right) ^{2}}{3 F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B} + 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}}} | ||
| + | \cdot \frac{P}{b} | ||
| + | </math> | ||
| + | <br /> | ||
| + | Eine ausführliche Herleitung dieser Formel ist in der Bautechnik, Mai 1969<ref name="Kanya" /> angegeben. | ||
| + | <br /> | ||
| + | Beim scharfen hinsehen erkennt man, dass einige Terme wiederholt in der Gleichung vorkommen. Damit diese lange Gleichung bei der Berechnung nicht jedes mal komplett eingegeben werden muss, wurden verschiedene Vorwerte definiert, die die Formel vereinfachen. | ||
| + | <br /> | ||
| + | ;Vorwerte | ||
| + | <br /> | ||
| + | :<math>\alpha = 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}}</math> | ||
| + | :<math>\beta = a - \frac{d}{2}</math> | ||
| + | :<math>\gamma = \frac{P}{b}</math> | ||
| + | :<math>\delta = \frac{2 \cdot \beta^{2}}{3 \cdot F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B}</math> | ||
| + | <br /> | ||
| + | Mit Hilfe dieser Vorwerte lauten die Berechnungsformeln für die anderen Größen wie folgt: | ||
| + | <br /> | ||
| + | ;Berechnungsformeln | ||
| + | <br /> | ||
| + | :<math>\sigma_{2} = \frac{\frac{2}{3} \cdot b^{2} - c \cdot b + \delta + \alpha}{\frac{b^{2}}{6} + \delta + \alpha} \cdot \gamma</math> | ||
| + | :<math>\sigma_{1} = 2 \cdot \gamma - \sigma_{2}</math> | ||
| + | :<math>M_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \alpha</math> | ||
| + | :<math>H_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \frac{\delta}{\beta}</math> | ||
<br /> | <br /> | ||
| + | ==Beispiel== | ||
| + | ;Berechnung eines Randstreifenfundaments | ||
| + | Ein Berechnungsbeispiel ist auf der Seite: [[Bemessung eines Randstreifenfundaments (Bsp.)|Bemessung eines Randstreifenfundaments (Bsp.)]] zu finden. | ||
| + | <br/> | ||
| + | ==Quellen== | ||
| + | <references /> | ||
| + | <br/> | ||
| + | <br/> | ||
{{Seiteninfo(mb) | {{Seiteninfo(mb) | ||
| Zeile 52: | Zeile 128: | ||
|Status = Seite fertig, ungeprüft| | |Status = Seite fertig, ungeprüft| | ||
|Modul-Version = 2020.0150}} | |Modul-Version = 2020.0150}} | ||
| + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | ||
Aktuelle Version vom 26. Februar 2025, 23:01 Uhr
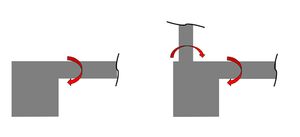
Das Berechnungsverfahren nach Josef Kanya beschäftigt sich mit dem Spezialfall des exzentrisch belasteten Streifenfundaments. In der Baupraxis kann die Situation auftreten, in der ein Randstreifenfundament direkt an/auf der Grundstücksgrenze errichtet werden muss. Damit die maximale Grundfläche des Gebäudes ausgeschöpft werden kann, versucht man die aufgehenden Wände so weit wie möglich an den Rand des Fundaments zu setzen. Es liegt nahe, dass die zulässige Exzentrizität schnell überschritten wird und sehr hohe Sohldruckspannungen am äußeren Rand auftreten. Um dem entgegenzuwirken, wurden von Freihart [1] und Watermann [2] Berechnungsmethoden auf Grundlage des Spannungstrapezverfahrens entwickelt, die Momente von biegesteif angeschlossenen Platten und Wänden (auch Zentrierplatte bzw. Zentriermoment genannt) berücksichtigen. Dadurch werden der Wert der Exzentrizität stark verbessert und schädliche Verformungen verhindert. Kanya[3] hat diese Methoden aufgegriffen und auf dieser Grundlage Berechnungsformeln entwickelt, die auch die vorher nicht berücksichtigte Zentrierzugkraft und die Verschiebung des Fundamentschwerpunktes beinhalten.
Voraussetzungen
Damit die Berechnungsformeln angewandt werden können, müssen einige Voraussetzungen geprüft bzw. erfüllt sein:
- Die gesamte Gründung erfährt im Fundamentschwerpunkt die gleiche mittlere Setzung.
- Das zu berechnende Randfundament verdreht sich um den Punkt D
- Das nebenliegende Mittelfundament ist verdrehungssteif.
- Es besteht ein „reines“ System, keine Verbindungsfundamente parallel zur Plattentragrichtung
- Die Zentrierplatte muss fachgerecht bewehrt und weich gelagert sein. Zusätzlich darf sie nicht durch fremde Einwirkungen beansprucht sein.
- Das Randstreifenfundament hat eine Steifigkeit von Ks →ꝏ
- Die Eigenlast der Zentrierplatte soll im Verhältnis zur angreifenden Last vernachlässigbar klein sein.
Formelzeichen
Für das bessere Verständnis der Berechnungsformeln folgt eine Tabelle mit der Auflistung aller verwendeten Formelzeichen in den Gleichungen.
| Formelzeichen | Einheit | Beschreibung |
|---|---|---|
| EB | kN/cm2 | Elastizitätsmodul des Stahlbetons |
| FB | cm2 | Querschnittsfläche 1 cm breiter Zentrierplatte |
| IB | cm4 | Trägheitsmoment 1 cm breiter Zentrierplatte |
| Es | kN/cm2 | Steifemodul des Bodens |
| a | cm | Höhe des Randfundaments |
| b | cm | Breite des Randfundaments |
| c | cm | Randabstand der Last P |
| d | cm | Dicke der Zentrierplatte |
| l | cm | lichte Spannweite der Zentrierplatte |
| P | kN/cm | Belastung pro lfd. cm |
| M1 | kNcm/cm | Moment in der Sohlfuge durch HZ |
| HB | kN/cm | Reibungskraft in der Sohlfuge pro lfd. cm |
| σ1 | kN/cm2 | Sohlspannung Innenkante Randfundament |
| σ2 | kN/cm2 | Sohlspannung Außenkante Randfundament |
| MZ | kNcm/cm | Zentriermoment pro lfd. cm |
| HZ | kN/cm | Zentrierzugkraft pro lfd. cm |
Formeln
Zur Lösung werden die Gleichungen der Kräftesummen in der Sohlfuge aufgestellt.
- Grundbedingungen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum M=0 \to P \cdot f-M_{1}-M_{z}=0}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum H=0 \to H_{B} - H_{Z}=0}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sum V=0 \to P = \frac{\sigma_{1}+\sigma_{2}}{2} \cdot b}
Durch Umformung und Einsetzen der Größen aus der vorherigen Tabelle erhält man die Gleichung für σ2.
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{2} = \frac {\frac{2}{3} \cdot b^{2} - c \cdot b + \frac{2 \cdot \left( a - \frac{d}{2} \right) ^{2}}{3 F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B} + 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}}} {\frac{b^{2}}{6} + \frac{2 \cdot \left( a - \frac{d}{2} \right) ^{2}}{3 F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B} + 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}}} \cdot \frac{P}{b} }
Eine ausführliche Herleitung dieser Formel ist in der Bautechnik, Mai 1969[3] angegeben.
Beim scharfen hinsehen erkennt man, dass einige Terme wiederholt in der Gleichung vorkommen. Damit diese lange Gleichung bei der Berechnung nicht jedes mal komplett eingegeben werden muss, wurden verschiedene Vorwerte definiert, die die Formel vereinfachen.
- Vorwerte
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta = a - \frac{d}{2}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma = \frac{P}{b}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta = \frac{2 \cdot \beta^{2}}{3 \cdot F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B}}
Mit Hilfe dieser Vorwerte lauten die Berechnungsformeln für die anderen Größen wie folgt:
- Berechnungsformeln
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{2} = \frac{\frac{2}{3} \cdot b^{2} - c \cdot b + \delta + \alpha}{\frac{b^{2}}{6} + \delta + \alpha} \cdot \gamma}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{1} = 2 \cdot \gamma - \sigma_{2}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \alpha}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \frac{\delta}{\beta}}
Beispiel
- Berechnung eines Randstreifenfundaments
Ein Berechnungsbeispiel ist auf der Seite: Bemessung eines Randstreifenfundaments (Bsp.) zu finden.
Quellen
- ↑ G. Freihart, „Die Ermittlung der maximalen Bodenpressung unter Grenzmauerfundamenten,“ Die Bautechnik, pp. 394-396, November 1962
- ↑ G. Watermann, „Zur Berechnung ausmittig belasteter Streifenfundamente,“ Die Bautechnik, pp. 61-62, Februar 1967
- ↑ 3,0 3,1 J. Kanya, „Berechnung ausmittig belasteter Streifenfundamente mit Zentrierung durch eine Stahlbeton-Fußbodenplatte,“ Die Bautechnik, pp. 154-159, Mai 1969
Seiteninfo
|