Verformungsnachweis: Unterschied zwischen den Versionen
Gbolle (Diskussion | Beiträge) K |
EWill (Diskussion | Beiträge) K |
||
| Zeile 1: | Zeile 1: | ||
| − | [[File:Verformungsnachweis_1.jpg|right|thumb|300px|Verformungen eines Einfeldträgers unter einer Einzellast]]Der Verformungsnachweis bzw. Durchbiegungsnachweis zählt zu den Nachweisen im Grenzzustand der Gebrauchstauglichkeit. | + | [[File:Verformungsnachweis_1.jpg|right|thumb|300px|Verformungen eines Einfeldträgers unter einer Einzellast]]Der Verformungsnachweis bzw. Durchbiegungsnachweis zählt zu den Nachweisen im Grenzzustand der Gebrauchstauglichkeit. Die folgenden Ausführungen beziehen sich auf [[überwiegend biegebeanspruchter Querschnitt|überwiegend biegebeanspruchte Querschnitte]]. |
<br /> | <br /> | ||
| Zeile 73: | Zeile 73: | ||
=Nachweis= | =Nachweis= | ||
| − | Der Verformungsnachweis kann entweder mittels einer [[ | + | Der Verformungsnachweis kann entweder mittels einer [[Verformungsnachweis - direkte Berechnung|direkten Verformungsberechnung]] oder indirekt über die [[Verformungsnachweis - indirekte Berechnung|Biegeschlankheit]] geführt werden. |
Nachweis über eine direkte Verformungsberechnung: | Nachweis über eine direkte Verformungsberechnung: | ||
| Zeile 82: | Zeile 82: | ||
:{| | :{| | ||
|- | |- | ||
| − | | <math> f_{vorh} </math> … || vorhandene Durchbiegung (vgl. [[ | + | | <math> f_{vorh} </math> … || vorhandene Durchbiegung (vgl. [[Verformungsnachweis - direkte Berechnung|direkte Verformungsberechnung]]) |
|- | |- | ||
| <math> f_{zul}\leq\frac{l}{250} </math> … || zulässige Verformung | | <math> f_{zul}\leq\frac{l}{250} </math> … || zulässige Verformung | ||
| Zeile 96: | Zeile 96: | ||
:{| | :{| | ||
|- | |- | ||
| − | | <math> \left(\frac{l}{d}\right)_{zul} </math> … || zulässige Biegeschlankheit (vgl. [[ | + | | <math> \left(\frac{l}{d}\right)_{zul} </math> … || zulässige Biegeschlankheit (vgl. [[Verformungsnachweis - indirekte Berechnung|indirekten Verformungsberechnung]]) |
|- | |- | ||
| − | | <math> \left(\frac{l}{d}\right)_{vorh} </math> … || vorhandene Biegeschlankheit (vgl. [[ | + | | <math> \left(\frac{l}{d}\right)_{vorh} </math> … || vorhandene Biegeschlankheit (vgl. [[Verformungsnachweis - indirekte Berechnung|indirekten Verformungsberechnung]]) |
|}</li> | |}</li> | ||
| − | Nähere Informationen zur zulässigen Biegeschlankheit sind der Seite zur [[ | + | Nähere Informationen zur zulässigen Biegeschlankheit sind der Seite zur [[Verformungsnachweis - indirekte Berechnung|indirekten Verformungsberechnung]] zu entnehmen. |
I. d. R. ist der Nachweis über die Biegeschlankheit ausreichend, ist aber eine genauere Kenntnis über selbige erforderlich oder kann der Verformungsnachweis über die Biegeschlankheit nicht erfüllt werden, kann eine direkte Verformungsberechnung sinnvoll sein, da diese genauere Ergebnisse liefert. Nachteil der direkten Verformungsberechnung ist der höhere Rechenaufwand. | I. d. R. ist der Nachweis über die Biegeschlankheit ausreichend, ist aber eine genauere Kenntnis über selbige erforderlich oder kann der Verformungsnachweis über die Biegeschlankheit nicht erfüllt werden, kann eine direkte Verformungsberechnung sinnvoll sein, da diese genauere Ergebnisse liefert. Nachteil der direkten Verformungsberechnung ist der höhere Rechenaufwand. | ||
Aktuelle Version vom 11. Januar 2025, 23:59 Uhr
Der Verformungsnachweis bzw. Durchbiegungsnachweis zählt zu den Nachweisen im Grenzzustand der Gebrauchstauglichkeit. Die folgenden Ausführungen beziehen sich auf überwiegend biegebeanspruchte Querschnitte.
Allgemeines
Eine Begrenzung der Verformungen ist erforderlich, um die Funktionalität bzw. die Gebrauchstauglichkeit eines Bauteils sicherzustellen. Durch die übermäßige Verformung eines Bauteils können auch Schäden an angrenzenden Bauteilen auftreten z.B. an Trennwänden oder Schaufenstern. Ein weiterer Grund für den Verformungsnachweis ist die Vermeidung optischer Beeinträchtigungen, sodass ein vertrauenswürdiges Erscheinungsbild gewahrt werden kann.
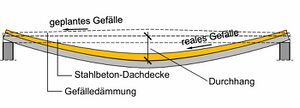
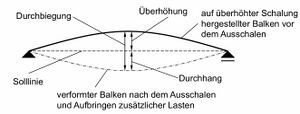
Im Rahmen des Verformungsnachweises wird zwischen dem Durchhang und der Durchbiegung unterschieden. Der Durchhang ist die vertikale Verformung des Bauteils bezogen auf die geradlinige Verbindung der Unterstützungspunkte. Die Durchbiegung ist die vertikale Verformung bezogen auf den Ursprungszustand der Systemlinie.
Die Unterscheidung zwischen Durchhang und Durchbiegung ist beispielsweise von Bedeutung, wenn das Bauteil mit einer Überhöhung eingebaut wurde.
Abhängig vom Nachweisziel kann der überhöhte Einbau eines Bauteils einen positiven Effekt haben, da dadurch der Durchhang geringer ist . Auf die Durchbiegung hat eine Überhöhung keinen Einfluss.
Einflüsse auf die Verformung
Generell wird die Verformung durch alle Faktoren beeinflusst, die die Dehnungen und somit auch die Krümmung eines Bauteils beeinflussen. Grund hierfür ist der Zusammenhang zwischen Belastung und Krümmung. Im Folgenden wird auf die wichtigsten Einflussfaktoren für die Verformungen eingegangen:
Material
Die Verformung wird maßgeblich durch die Festigkeit und die zeitlich veränderlichen Eigenschaften (z.B. Kriechen und Schwinden) der verwendeten Materialien beeinflusst. Der Einfluss des Betons ist hierbei bedeutender als der der Bewehrung. Von der Zugfestigkeit des Betons ist abhängig, wann das Bauteil in den Zustand II übergeht. Je größer die Zugfestigkeit des Betons ist, desto kleiner ist der Bereich des Bauteils, der sich im Zustand II befindet und desto kleiner ist die Verformung. Auf den Einfluss von Kriechen und Schwinden wird in separaten Abschnitten eingegangen.
Unter Dauerblastung nimmt die wirksame Zugfestigkeit mit der Zeit ab, sodass sich der Bereich der sich im Zustand II befindet vergrößert. Gleiches gilt wegen des Zusammenhangs zwischen Steifigkeit und Verformung auch für die Verformungen [1]. Dieser Umstand ist bei der Berechnung zu berücksichtigen (vgl. Belastungsgeschicht).
Bauteilgeometrie
Die Größe der auftretenden Verformung ist maßgeblich abhängig von den Flächenträgheitsmomenten und somit auch von der Bauteilhöhe und Breite. Mit steigender Bauteilhöhe und Bauteilbreite nehmen die Verformungen ab. Der Einfluss der Bauteilbreite ist dabei geringer als der der Höhe. Dies lässt sich auch an der Gleichung für die Ermittlung des Flächenträgheitsmoments deutlich erkennen.
wobei:
… Breite … Höhe
Mit zunehmender Systemlänge nehmen die Verformungen zu.
Bewehrungslage/-menge
Auch die Lage und Menge der Bewehrung hat einen Einfluss auf das Flächenträgheitsmoment und somit auf die Verformungen. Je größer der Abstand der Bewehrung vom Schwerpunkt ist und je mehr Bewehrung vorhanden ist, desto größer wird das Flächenträgheitsmoment. Der Einfluss der Bewehrung auf die Bauteilsteifigkeit spielt allerdings erst im Zustand II eine größere Rolle, im Zustand I ist ihr Einfluss unbedeutend gering.
Mit zunehmender Menge an Bewehrung sinkt bei gleicher Belastung außerdem die Stahldehnungen, sodass die Krümmungen und somit auch die Verformungen abnehmen.
Belastung
Mit steigender Belastung vergrößert sich der Bereich der sich im Zustand II befindet, sodass die Steifigkeit abnimmt und die Verformungen zunehmen. Unter kurzzeitiger Belastung treten kleinere Verformungen auf als unter langzeitiger.
Belastungsgeschichte
Wenn ein Bauteil einmal in den gerissenen Zustand übergegangen ist, nimmt die Steifigkeit irreversibel ab. Sinkt die Last wieder unter die Last, bei der es zur Rissbildung kommt, nimmt die Steifigkeit nicht wieder zu. Wenn das Bauteil planmäßig Lasten ausgesetzt ist, welche zur Rissbildung führen oder wenn dies nicht ausgeschlossen werden kann, ist diesem Umstand bei der Verformungsberechnung durch Vergrößerung des Bereichs im Zustand II Rechnung zu tragen, auch wenn unter den Lasten, die der Berechnung zu Grunde liegen keine Risse entstehen.
Berücksichtigen lässt sich die Belastungsgeschichte indem die Größe des Bereichs im Zustand II unter seltener Einwirkungskombination bei Ansatz der Kurzzeitzugfestigkeit ermittelt wird. Die Berücksichtigung der Verringerung der wirksamen Zugfestigkeit ist bei dieser Variante nicht erforderlich, da davon ausgegangen wird, dass die Vergrößerung des Bereichs im Zustand II mithilfe dieses Modells ausreichend ist [1].
Die Verformung wird außerdem maßgeblich durch den Erstbelastungszeitpunkt beeinflusst. Ist dieser nach 14 Tagen bzw. später ist der Einfluss nur gering, findet die Erstbelastung allerdings früher statt, hat dies einen deutlichen Einfluss auf die Verformungen. So ist steigt die Durchbiegung beispielsweise um ca. 28% an bei einer Erstbelastung nach drei Tagen im Vergleich zu einer solchen nach 28 Tagen [2].
Kriechen
Unter Kriechen versteht man die zeitabhängige Verformungszunahme unter konstanter Belastung. Auf die Grundlagen für und die Einflüsse auf das Kriechen wird auf einer gesonderten Seite eingegangen. Allgemein lässt sich feststellen, dass je größer der Kriecheinfluss ist, desto mehr nehmen die Verformungen zu. Berücksichtigt werden kann der Kriecheinfluss durch die Abminderung des Elastizitätsmoduls mithilfe der Kriechzahl.
Schwinden
Auch für nähere Informationen zum Schwinden steht eine gesonderte Seite zur Verfügung. Der Einfluss des Schwindens auf die Verformungen resultiert aus der unterschiedlich stark behinderten Schwindverformung durch die Bewehrung über die Querschnittshöhe. Im Zugbereich wird die Schwindverformung durch die Zugbewehrung behindert. Ist im Druckbereich keine oder nur wenig Bewehrung vorhanden, finden die Schwindverformungen ungehindert statt. Durch die unterschiedlichen Dehnungen an Bauteilober- und -unterseite entsteht eine Krümmung und infolgedessen eine Durchbiegung. Die größere Krümmung wird rechnerisch durch einen zusätzlichen Krümmungsanteil berücksichtigt.
Die Krümmungen infolge Schwinden sind belastungsunabhängig, sie hängen nur von der Bauteilgeometrie ab. Die Krümmungen infolge Schwinden sind somit bei konstantem Querschnitt über die Bauteillänge bekannt.
Temperatur
Die Temperatur teilt sich in einen konstanten und einen linearen Anteil auf. Der konstante Anteil führt zu einer konstanten Verformung (statisch bestimmte Systeme) bzw. Spannung (statisch unbestimmte Systeme) über die Querschnittshöhe. Der lineare Temperaturanteil entsteht, wenn eine Seite wärmer bzw. kälter ist als die andere, hieraus resultiert eine veränderliche Dehnung über die Querschnittshöhe und somit eine Krümmung. Wegen des allgemeinen Zusammenhangs von Krümmung und Durchbiegung, entsteht infolgedessen auch eine Durchbiegung.
Mitwirkung des Betons zwischen den Rissen
Zwischen den Rissen werden die Zugkräfte aus dem Beton wieder in den Beton übertragen, wodurch die Stahldehnung abnimmt. Wird die Mitwirkung des Betons zwischen den Rissen nicht berücksichtigt, wird die Verformung überschätzt, da die Krümmung überschätzt wird. Berücksichtigt werden kann sie über den Verteilungsbeiwert.
Nachweis
Der Verformungsnachweis kann entweder mittels einer direkten Verformungsberechnung oder indirekt über die Biegeschlankheit geführt werden.
Nachweis über eine direkte Verformungsberechnung:
wobei:
… vorhandene Durchbiegung (vgl. direkte Verformungsberechnung) … zulässige Verformung
Grenzen an das betrachtete Bauteil verformungsempfindliche Bauteile an (z.B. Trennwände) ist die Durchbiegung w außerdem auf l/500 zu begrenzen.
Nachweis über die Biegeschlankheit:
wobei:
… zulässige Biegeschlankheit (vgl. indirekten Verformungsberechnung) … vorhandene Biegeschlankheit (vgl. indirekten Verformungsberechnung)
Nähere Informationen zur zulässigen Biegeschlankheit sind der Seite zur indirekten Verformungsberechnung zu entnehmen.
I. d. R. ist der Nachweis über die Biegeschlankheit ausreichend, ist aber eine genauere Kenntnis über selbige erforderlich oder kann der Verformungsnachweis über die Biegeschlankheit nicht erfüllt werden, kann eine direkte Verformungsberechnung sinnvoll sein, da diese genauere Ergebnisse liefert. Nachteil der direkten Verformungsberechnung ist der höhere Rechenaufwand.
Die in der Norm angegebenen Grenzwerte sind nur als Empfehlungen zu sehen. Die im Einzelfall geltenden Grenzwerte sind mit dem Bauherrn abzusprechen. Teilweise sind die Verformungen stärker zu begrenzen z.B. wenn die Funktionsfähigkeit von Maschinen oder der Entwässerung von Flachdächern sichergestellt werden muss, teilweise können die Grenzwerte in der Norm aber auch überschritten werden, wenn durch größere Verformungen kein Mangel entsteht.
Die Last, unter der der Verformungsnachweis zu führen ist, ist ebenfalls vom Einzelfall abhängig; gibt es keine speziellen Randbedingungen, empfiehlt sich die Verwendung der quasi-ständigen Lastkombination.
Quellen
Seiteninfo
|