Knicklänge/Ersatzstablänge: Unterschied zwischen den Versionen
Gbolle (Diskussion | Beiträge) K |
|||
| (17 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | + | <br /> | |
| − | + | Die Ersatz-(stab)länge und die Knicklänge bezeichnen beide dasselbe Maß zwischen den Wendepunkten der Knickbiegelinie eines Druckstabs. Die Form der Verformungsfigur gleicht dabei grundsätzlich einer Sinus-Kurve [vgl. <ref Name = "Schneider">Schneider, K.-J.: Bautabellen für Ingenieure, Siegen 2010</ref>]. Sie bestimmt sich nach<br /> | |
| − | <math>{{l}_{0}} | + | :<math>{{l}_{0}}=\beta \cdot {{l}_{col}}</math><br /> |
| − | < | + | wobei:<br /> |
| − | <math>{{l}_{col}}</math> | + | :{| |
| + | |- | ||
| + | | <math>{{l}_{0}}</math>… || Knicklänge oder Ersatzlänge (andere Schreibweisen: <math>{{L}_{cr}}</math> oder <math>{{s}_{k}}</math> (mit den Indizes critical und Knicken) | ||
| + | |- | ||
| + | | <math>\beta </math>… || Knicklängenbeiwert | ||
| + | |- | ||
| + | | <math>{{l}_{col}}</math>… || Stützenhöhe (Länge des Stabs zwischen den idealisierten Einspannstellen mit Index column | ||
| + | |}<br /> | ||
| − | „Für die Bestimmung der Ersatzlänge <math>{{l}_{0}}</math> gilt, dass sich unter sonst gleichen Bedingungen für unterschiedliche Systeme gleich große Verformungen nach [[Theorie II. Ordnung|Theorie II. Ordnung]] ergeben.“ | + | „Für die Bestimmung der Ersatzlänge <math>{{l}_{0}}</math> gilt, dass sich unter sonst gleichen Bedingungen für unterschiedliche Systeme gleich große Verformungen nach [[Theorie II. Ordnung|Theorie II. Ordnung]] ergeben.“ <ref>Wommelsdorff, O., Albert, A.: Stahlbetonbau, Bemessung und Konstruktion Teil 2: Stützen, Sondergebiete des Stahlbetonbaus, Oer-Erkenschwick 2005</ref><br /> |
| − | Abhängig von den Auflagerbedingungen des [[Einzeldruckglied|Einzeldruckglieds]] und der | + | Abhängig von den Auflagerbedingungen des [[Einzeldruckglied|Einzeldruckglieds]] und der gegenseitigen Verschieblichkeit der Stützenenden senkrecht zur Bauteilachse bestimmt sich der Knicklängenbeiwert β. Bei idealer Lagerung ist er anhand der vier Eulerfälle einfach zu bestimmen:<br /><br /> |
[[File:Knicklängen_Ersatzstablängen_1.jpg|rahmenlos|rand|tumb|1000px|Baustatik-Wiki]]<br /> | [[File:Knicklängen_Ersatzstablängen_1.jpg|rahmenlos|rand|tumb|1000px|Baustatik-Wiki]]<br /> | ||
| Zeile 20: | Zeile 26: | ||
β (realistisch): 2,2 1,0 0,76 0,59<br /><br /> | β (realistisch): 2,2 1,0 0,76 0,59<br /><br /> | ||
| − | Für die Praxis reichen | + | Die realistischen Beiwerte β berücksichtigen den Sachverhalt, dass eine unendlich feste Einspannung in der Praxis nicht existiert. Auch bei einer sehr steifen Einspannung sind immer geringe Verformungen nötig, um das entsprechende Einspannmoment zu aktivieren.<br /> |
| + | |||
| + | Für die Praxis reichen die angegebenen 4 Grundfälle allerdings nicht aus, oft sind die Stützen elastisch eingespannt, Teil eines Rahmens oder eines verschieblichen Gesamtsystems. Bei einem verschieblichen System, also senkrecht zur Bauteilachse gegeneinander verschieblichen Endauflagern, sind die Knicklängen in der Realität stets größer als die Stablänge [vgl. <ref>Lohmeyer, G., Baar S., Ebeling, G.: Stahlbetonbau, Bemessung – Konstruktion – Ausführung, Hannover 2012</ref>]. Ein verschiebliches und ein unverschiebliches System mit ihren dazugehörigen Knicklängen sind in folgender Abbildung gezeigt.<br /><br /> | ||
[[File:Knicklängen_Ersatzstablängen_2.jpg|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | [[File:Knicklängen_Ersatzstablängen_2.jpg|rahmenlos|rand|tumb|700px|Baustatik-Wiki]]<br /> | ||
<br /> | <br /> | ||
| − | Das Flächenträgheitsmoment ist hier als unendlich groß beschrieben, woraus für die Rahmenstiele an beiden Enden eine starre Einspannung resultiert. In der Praxis kommt es weder zu einem unendlich großen Flächenträgheitsmoment am Endpunkt eines Stiels noch zu einer 100%igen starren Einspannung | + | Das Flächenträgheitsmoment des Riegels ist hier als unendlich groß beschrieben, woraus für die Rahmenstiele an beiden Enden eine starre Einspannung resultiert. In der Praxis kommt es weder zu einem unendlich großen Flächenträgheitsmoment des Riegels am Endpunkt eines Stiels noch zu einer 100%igen starren Einspannung (siehe oben). <br /> |
Zur Ermittlung des Knickbeiwertes wird demnach grundsätzlich nach Verschieblichkeit unterschieden und der Einfluss der angeschlossenen Bauteile am Stützenende, genauer gesagt die Elastizität jener im Verhältnis zur Steifigkeit der Stütze, berücksichtigt. <br /> | Zur Ermittlung des Knickbeiwertes wird demnach grundsätzlich nach Verschieblichkeit unterschieden und der Einfluss der angeschlossenen Bauteile am Stützenende, genauer gesagt die Elastizität jener im Verhältnis zur Steifigkeit der Stütze, berücksichtigt. <br /> | ||
| − | Der Eurocode 2 zwei Gleichungen zur Ermittlung der Knicklänge bei „[[Regelmäßige Rahmen|üblichen]]“ Rahmen vor:<br /><br /> | + | Der Eurocode 2 gibt zwei Gleichungen zur Ermittlung der Knicklänge bei „[[Regelmäßige Rahmen|üblichen]]“ Rahmen vor:<br /><br /> |
für unverschiebliche Rahmen:<br /> | für unverschiebliche Rahmen:<br /> | ||
| − | <math>{{l}_{0}}=0,5\cdot l\cdot \sqrt{\left( 1+\frac{{{k}_{1}}}{0,45+{{k}_{1}}} \right)\cdot \left( 1+\frac{{{k}_{2}}}{0,45+{{k}_{2}}} \right)}</math> | + | :{| |
| + | |<math>{{l}_{0}}=0,5\cdot l\cdot \sqrt{\left( 1+\frac{{{k}_{1}}}{0,45+{{k}_{1}}} \right)\cdot \left( 1+\frac{{{k}_{2}}}{0,45+{{k}_{2}}} \right)}</math> | ||
| + | |}<br /> | ||
für verschiebliche Rahmen:<br /> | für verschiebliche Rahmen:<br /> | ||
| + | :{| | ||
| + | |<math>{{l}_{0}}=l\cdot \max \left\{ \sqrt{1+10\cdot \frac{{{k}_{1}}\cdot {{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}}\ ;\ \left( 1+\frac{{{k}_{1}}}{1+{{k}_{1}}} \right)\cdot \left( 1+\frac{{{k}_{2}}}{1+{{k}_{2}}} \right) \right\}</math> | ||
| + | |}<br /> | ||
| − | |||
| − | |||
mit<br /> | mit<br /> | ||
| − | + | :{| | |
| − | <math>{{k}_{1}},{{k}_{2}}</math> - den jeweils bezogener Einspanngrade an den Enden 1 und 2 | + | |<math>{{k}_{1}},{{k}_{2}}</math> || - || den jeweils bezogener Einspanngrade an den Enden 1 und 2 |
| − | l | + | |- |
| + | |l || - || der lichten Höhe des Druckglieds zwischen den Endeinspannungen | ||
| + | |}<br /> | ||
Die Einspanngrade berechnen sich am Knotenpunkt der Stabenden aus dem Verhältnis der Stabsteifigkeit und dem Drehwiderstandsmoment infolge einer Knotendrehung <math>\varphi </math> (Einheitsdrehung <math>\varphi </math> = 1):<br /><br /> | Die Einspanngrade berechnen sich am Knotenpunkt der Stabenden aus dem Verhältnis der Stabsteifigkeit und dem Drehwiderstandsmoment infolge einer Knotendrehung <math>\varphi </math> (Einheitsdrehung <math>\varphi </math> = 1):<br /><br /> | ||
| + | [[File:Knicklängen_Ersatzstablängen_3.jpg|right|thumb|1000px|Nomogramm zur Ermittlung des Knicklängenbeiwertes<ref Name = "Schneider"> </ref>]] | ||
<math>{{k}_{i}}=\frac{\Sigma E{{I}_{col}}/{{l}_{col}}}{\Sigma {{M}_{R,i}}}</math> | <math>{{k}_{i}}=\frac{\Sigma E{{I}_{col}}/{{l}_{col}}}{\Sigma {{M}_{R,i}}}</math> | ||
mit<br /> | mit<br /> | ||
| − | E – dem Elastizitätsmodul | + | :{| |
| − | <math>{{I}_{col}}</math> – dem Flächenträgheitsmoment der Stütze | + | | E || – || dem Elastizitätsmodul |
| − | <math>{{l}_{col}}</math> – der Länge der Stütze | + | |- |
| − | <math>{{M}_{R,i}}</math> – dem Drehwiderstandsmoment (mit Index | + | |<math>{{I}_{col}}</math> || – || dem Flächenträgheitsmoment der Stütze |
| − | + | |- | |
| − | + | |<math>{{l}_{col}}</math> || – || der Länge der Stütze | |
| − | + | |- | |
| − | + | |<math>{{M}_{R,i}}</math> || – || dem Drehwiderstandsmoment (mit Index Resistance). | |
| − | <br /> | + | |}<br /> |
| + | Die nebenstehende Abbildung zeigt die Auswertung der beiden Gleichung des Eurocode 2 in Form eines Nomogramms:<br /><br /> | ||
Bei der Verwendung des Nomogramms kann das Flächenträgheitsmoment der anschließenden Stützen voll angesetzt werden, wohingegen wegen zu erwartender Rissbildung das der Riegel zur Hälfte angesetzt wird. | Bei der Verwendung des Nomogramms kann das Flächenträgheitsmoment der anschließenden Stützen voll angesetzt werden, wohingegen wegen zu erwartender Rissbildung das der Riegel zur Hälfte angesetzt wird. | ||
| − | Bei einer gelenkigen Lagerung wäre der Betrag für k = ∞, der Dividend also null, vergleichbar mit einem Riegel ohne jegliche Steifigkeit. Eine starre Einspannung entspräche einem k von 0 resultierend aus einem unendlich großen Dividenden (Drehsteifigkeit). Da, wie bereits erwähnt, eine Einspannung | + | Bei einer gelenkigen Lagerung wäre der Betrag für k = ∞, der Dividend also null, vergleichbar mit einem Riegel ohne jegliche Steifigkeit. Eine starre Einspannung entspräche einem k von 0 resultierend aus einem unendlich großen Dividenden (Drehsteifigkeit). Da, wie bereits erwähnt, eine absolut starre Einspannung praktisch nicht existiert, wird ein k kleiner als 0,1 nicht empfohlen. |
<br /> | <br /> | ||
==Quellen== | ==Quellen== | ||
| Zeile 67: | Zeile 82: | ||
{{Seiteninfo | {{Seiteninfo | ||
| − | |Quality-flag = [[File:quality-flag- | + | |Quality-flag = [[File:quality-flag-green.gif|right|70px]] |
| − | |Status = Seite | + | |Status = Seite geprüft, inhaltlich Ok |
}} | }} | ||
| − | [[Kategorie:Grundlagen/Begriffe]] | + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] |
Aktuelle Version vom 14. September 2020, 20:37 Uhr
Die Ersatz-(stab)länge und die Knicklänge bezeichnen beide dasselbe Maß zwischen den Wendepunkten der Knickbiegelinie eines Druckstabs. Die Form der Verformungsfigur gleicht dabei grundsätzlich einer Sinus-Kurve [vgl. [1]]. Sie bestimmt sich nach
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}=\beta \cdot {{l}_{col}}}
wobei:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}} … Knicklänge oder Ersatzlänge (andere Schreibweisen: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{L}_{cr}}} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{s}_{k}}} (mit den Indizes critical und Knicken) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta } … Knicklängenbeiwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{col}}} … Stützenhöhe (Länge des Stabs zwischen den idealisierten Einspannstellen mit Index column
„Für die Bestimmung der Ersatzlänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}}
gilt, dass sich unter sonst gleichen Bedingungen für unterschiedliche Systeme gleich große Verformungen nach Theorie II. Ordnung ergeben.“ [2]
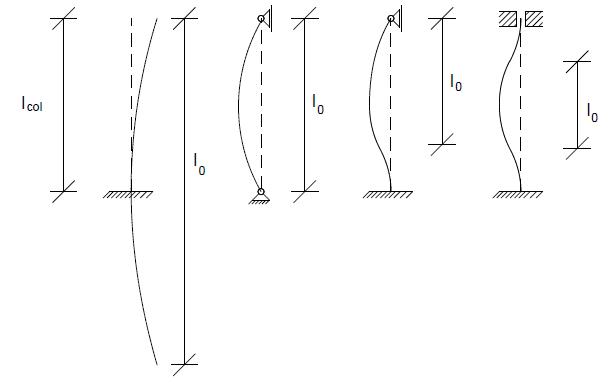
Abhängig von den Auflagerbedingungen des Einzeldruckglieds und der gegenseitigen Verschieblichkeit der Stützenenden senkrecht zur Bauteilachse bestimmt sich der Knicklängenbeiwert β. Bei idealer Lagerung ist er anhand der vier Eulerfälle einfach zu bestimmen:
β (theoretisch): 2,0 1,0 0,7 0,5
β (realistisch): 2,2 1,0 0,76 0,59
Die realistischen Beiwerte β berücksichtigen den Sachverhalt, dass eine unendlich feste Einspannung in der Praxis nicht existiert. Auch bei einer sehr steifen Einspannung sind immer geringe Verformungen nötig, um das entsprechende Einspannmoment zu aktivieren.
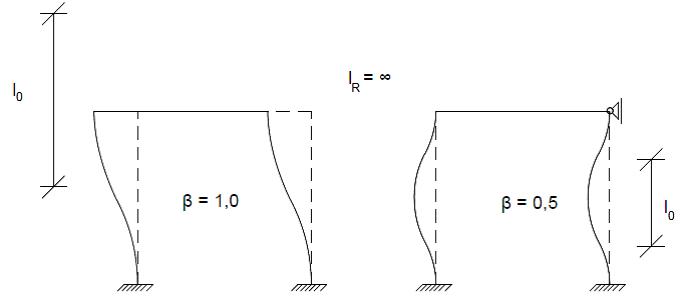
Für die Praxis reichen die angegebenen 4 Grundfälle allerdings nicht aus, oft sind die Stützen elastisch eingespannt, Teil eines Rahmens oder eines verschieblichen Gesamtsystems. Bei einem verschieblichen System, also senkrecht zur Bauteilachse gegeneinander verschieblichen Endauflagern, sind die Knicklängen in der Realität stets größer als die Stablänge [vgl. [3]]. Ein verschiebliches und ein unverschiebliches System mit ihren dazugehörigen Knicklängen sind in folgender Abbildung gezeigt.
Das Flächenträgheitsmoment des Riegels ist hier als unendlich groß beschrieben, woraus für die Rahmenstiele an beiden Enden eine starre Einspannung resultiert. In der Praxis kommt es weder zu einem unendlich großen Flächenträgheitsmoment des Riegels am Endpunkt eines Stiels noch zu einer 100%igen starren Einspannung (siehe oben).
Zur Ermittlung des Knickbeiwertes wird demnach grundsätzlich nach Verschieblichkeit unterschieden und der Einfluss der angeschlossenen Bauteile am Stützenende, genauer gesagt die Elastizität jener im Verhältnis zur Steifigkeit der Stütze, berücksichtigt.
Der Eurocode 2 gibt zwei Gleichungen zur Ermittlung der Knicklänge bei „üblichen“ Rahmen vor:
für unverschiebliche Rahmen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}=0,5\cdot l\cdot \sqrt{\left( 1+\frac{{{k}_{1}}}{0,45+{{k}_{1}}} \right)\cdot \left( 1+\frac{{{k}_{2}}}{0,45+{{k}_{2}}} \right)}}
für verschiebliche Rahmen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}=l\cdot \max \left\{ \sqrt{1+10\cdot \frac{{{k}_{1}}\cdot {{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}}\ ;\ \left( 1+\frac{{{k}_{1}}}{1+{{k}_{1}}} \right)\cdot \left( 1+\frac{{{k}_{2}}}{1+{{k}_{2}}} \right) \right\}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{k}_{1}},{{k}_{2}}} - den jeweils bezogener Einspanngrade an den Enden 1 und 2 l - der lichten Höhe des Druckglieds zwischen den Endeinspannungen
Die Einspanngrade berechnen sich am Knotenpunkt der Stabenden aus dem Verhältnis der Stabsteifigkeit und dem Drehwiderstandsmoment infolge einer Knotendrehung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi }
(Einheitsdrehung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi }
= 1):
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{k}_{i}}=\frac{\Sigma E{{I}_{col}}/{{l}_{col}}}{\Sigma {{M}_{R,i}}}}
mit
E – dem Elastizitätsmodul Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{I}_{col}}} – dem Flächenträgheitsmoment der Stütze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{col}}} – der Länge der Stütze Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{R,i}}} – dem Drehwiderstandsmoment (mit Index Resistance).
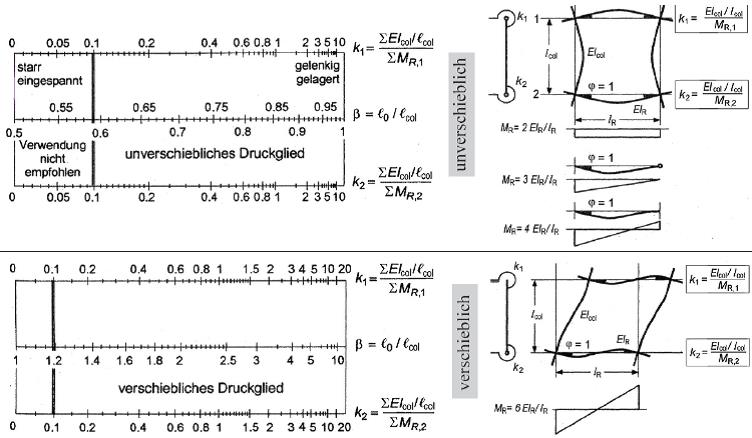
Die nebenstehende Abbildung zeigt die Auswertung der beiden Gleichung des Eurocode 2 in Form eines Nomogramms:
Bei der Verwendung des Nomogramms kann das Flächenträgheitsmoment der anschließenden Stützen voll angesetzt werden, wohingegen wegen zu erwartender Rissbildung das der Riegel zur Hälfte angesetzt wird.
Bei einer gelenkigen Lagerung wäre der Betrag für k = ∞, der Dividend also null, vergleichbar mit einem Riegel ohne jegliche Steifigkeit. Eine starre Einspannung entspräche einem k von 0 resultierend aus einem unendlich großen Dividenden (Drehsteifigkeit). Da, wie bereits erwähnt, eine absolut starre Einspannung praktisch nicht existiert, wird ein k kleiner als 0,1 nicht empfohlen.
Quellen
- ↑ 1,0 1,1 Schneider, K.-J.: Bautabellen für Ingenieure, Siegen 2010
- ↑ Wommelsdorff, O., Albert, A.: Stahlbetonbau, Bemessung und Konstruktion Teil 2: Stützen, Sondergebiete des Stahlbetonbaus, Oer-Erkenschwick 2005
- ↑ Lohmeyer, G., Baar S., Ebeling, G.: Stahlbetonbau, Bemessung – Konstruktion – Ausführung, Hannover 2012
Seiteninfo
|