Nachweisführung und Bewehrungsermittlung vergleichend zur MB-Baustatik (Ermittlung der Biegezugbewehrung): Unterschied zwischen den Versionen

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen
 
(3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 10: Zeile 10:
 
<math>\mu_\mathrm{Eds}=\cfrac{M_\mathrm{Eds}}{b_{f}\cdot d^2 \cdot f_\mathrm{cd}}= \cfrac{0,30382}{1,885\cdot 0,545^2 \cdot 19,8}= \underline{0,0274}</math>
 
<math>\mu_\mathrm{Eds}=\cfrac{M_\mathrm{Eds}}{b_{f}\cdot d^2 \cdot f_\mathrm{cd}}= \cfrac{0,30382}{1,885\cdot 0,545^2 \cdot 19,8}= \underline{0,0274}</math>
  
−
-Aus Tafel mit dimensionslosen Beiwerten für Rechteckquerschnitte:(interpoliert)
+
-Aus Tafel mit dimensionslosen Beiwerten für Rechteckquerschnitte:(interpoliert)<ref>Schneider Bautabellen für Ingenieure, 20. Auflage, Köln: Werner Verlag, 2012</ref>
  
 
<math>\xi = 0,052</math> &nbsp; <math>< h_{f}/d =0,366</math> &nbsp;&nbsp; &rArr; Nulllinie liegt in der Platte &nbsp; &rArr; &nbsp; Bemessung als Rechteck
 
<math>\xi = 0,052</math> &nbsp; <math>< h_{f}/d =0,366</math> &nbsp;&nbsp; &rArr; Nulllinie liegt in der Platte &nbsp; &rArr; &nbsp; Bemessung als Rechteck
Zeile 46: Zeile 46:
  
 
<div style="border: 2px solid blue; padding: 5px;">'''Hinweis:'''<br />
 
<div style="border: 2px solid blue; padding: 5px;">'''Hinweis:'''<br />
−
Bei der Bemessung der Biegezugbewehrung wird in der MB-Baustatik mit der Stahlzugfestigkeit unter der Berücksichtigung der Nachverfestigung ("ansteigender Ast" der Spannungs-Dehnungslinie) <math>f_{tk,cal}=525N/mm^2</math> gerechnet. Wenn in der Berechnung der "horizontale Ast" angenommen werden soll <math>(f_{yk}=500N/mm^2)</math>, beispielsweise für den besseren Vergleich mit einer Handrechnung, in der ein horizontaler Ast angenommen wurde oder für eine Berechnung auf der "sicheren Seite", kann der Wert in den Stammdaten verändert oder eine neue Stahlsorte definiert werden.
+
Bei der Bemessung der Biegezugbewehrung wird in der MB-Baustatik mit der Stahlzugfestigkeit unter der Berücksichtigung der Nachverfestigung ("ansteigender Ast" der Spannungs-Dehnungslinie) <math>f_{tk,cal}=525N/mm^2</math> gerechnet. Wenn in der Berechnung der "horizontale Ast" angenommen werden soll <math>(f_{yk}=500N/mm^2)</math>, beispielsweise für den besseren Vergleich mit einer Handrechnung, in der ein horizontaler Ast angenommen wurde oder für eine Berechnung auf der "sicheren Seite", kann der Wert in den Stammdaten verändert oder eine separate Stahlsorte definiert werden.
  
 
[[Datei:Ansteigender ast.PNG]] </div><br />
 
[[Datei:Ansteigender ast.PNG]] </div><br />
  
 
<div style="border: 2px solid blue; padding: 5px;">[[Datei:Ausgelagert.PNG|rechts]]'''Hinweis:'''<br />
 
<div style="border: 2px solid blue; padding: 5px;">[[Datei:Ausgelagert.PNG|rechts]]'''Hinweis:'''<br />
−
Das MB-Baustatikmodul S340.de verteilt die ermittelte Zugbewehrung im Bereich negativer Momente ausschließlich im Stegbereich. Dies ist allerdings nicht zu empfehlen, da diese hohe Bewehrungskonzentration im Stegbereich, zu breiten Rissen in der Platte führt. Es wird daher im Eurocode 2 empfohlen, ca. 50% der Zugbewehrung in diesen Bereichen, auf die Hälfte der rechnerischen Gurtbreite <math>b_{eff,i}</math> zu verteilen. Eine solche Bewehrungsverteilung führt zu einem günstigeren Rissbild und einem besseren Tragverhalten des Bauteils.  
+
Das MB-Baustatikmodul S340.de verteilt die ermittelte Zugbewehrung im Bereich negativer Momente ausschließlich im Stegbereich. Dies ist allerdings nicht zu empfehlen, da diese hohe Bewehrungskonzentration im Stegbereich, zu breiten Rissen in der Platte führt. Es wird daher im Eurocode 2 empfohlen, ca. 50% der Zugbewehrung in diesen Bereichen, auf die Hälfte der rechnerischen Gurtbreite <math>b_{eff,i}</math> zu verteilen. Eine solche Bewehrungsverteilung führt zu einem günstigeren Rissbild und einem besseren Tragverhalten des Bauteils.<ref>DIN EN 1992-1-1: Bemessung und Konstruktion von Stahlbeton und Spannbetontragwerken, Berlin: Beuth, 2010-2012</ref> <ref>Deutscher Ausschuss für Stahlbeton, Heft 600, Erläuterungen zu DIN EN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode), Berlin, 2012</ref>
  
  
Zeile 59: Zeile 59:
  
 
</div><br />
 
</div><br />
 +
  
 
==Quellen==
 
==Quellen==
 +
 +
<references/>
 +
 +
{{Seiteninfo(mb)
 +
|Quality-flag = [[File:quality-flag-white.gif|right|70px]]
 +
|Status = in Bearbeitung|
 +
|Modul-Version = 2016.0500}}

Aktuelle Version vom 2. Mai 2016, 15:23 Uhr

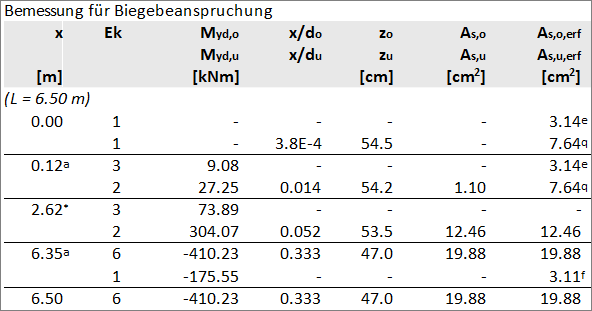
Ermittlung der Biegezugbewehrung

  • Feldbewehrung:


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Eds} = M_{Ed}} (Keine Normalkraft)

-bezogenes Moment:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_\mathrm{Eds}=\cfrac{M_\mathrm{Eds}}{b_{f}\cdot d^2 \cdot f_\mathrm{cd}}= \cfrac{0,30382}{1,885\cdot 0,545^2 \cdot 19,8}= \underline{0,0274}}

-Aus Tafel mit dimensionslosen Beiwerten für Rechteckquerschnitte:(interpoliert)[1]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi = 0,052}   Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle < h_{f}/d =0,366}    ⇒ Nulllinie liegt in der Platte   ⇒   Bemessung als Rechteck

-weiterhin:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega = 0,0279}      

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}= \cfrac{1}{\sigma_{sd}}\cdot (\omega \cdot b_{f}\cdot d\cdot f_{cd})= \cfrac{1}{457}\cdot (0,0279 \cdot 188,5\cdot 54,5\cdot 19,8)= \underline\underline{{12,42cm^2}}}


⇒ gewählt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{ 4 \varnothing 20}}     Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh}=12,6cm^2}


  • Bewehrung am Zwischenauflager:


Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \mu _{\mathrm {Eds} }={\cfrac {M_{\mathrm {Eds} }}{b_{f}\cdot d^{2}\cdot f_{\mathrm {cd} }}}={\cfrac {0,41487}{0,3\cdot 0,545^{2}\cdot 19,8}}={\underline {0,235}}}


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega = 0,273}       Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{sd}=439,5 N/mm^2}


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}= \cfrac{1}{\sigma_{sd}}\cdot (\omega \cdot b_{f}\cdot d\cdot f_{cd})= \cfrac{1}{439,5}\cdot (0,273 \cdot 30\cdot 54,5\cdot 19,8)= \underline\underline{{20,09cm^2}}}


⇒ gewählt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \underline{ 7 \varnothing 20}}     Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh}=22,0cm^2}


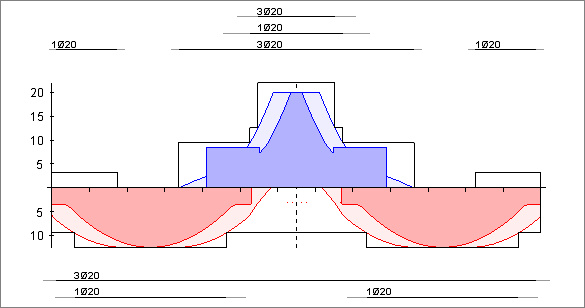
-Vergleich MB_Baustatik:                                   -Zugkraftdeckungslinie und Bewehrungsanordnung:

Erforderliche Längsbewehrung.PNG          Zugkraftdeckung1.PNG


Hinweis:

Bei der Bemessung der Biegezugbewehrung wird in der MB-Baustatik mit der Stahlzugfestigkeit unter der Berücksichtigung der Nachverfestigung ("ansteigender Ast" der Spannungs-Dehnungslinie) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{tk,cal}=525N/mm^2} gerechnet. Wenn in der Berechnung der "horizontale Ast" angenommen werden soll Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (f_{yk}=500N/mm^2)} , beispielsweise für den besseren Vergleich mit einer Handrechnung, in der ein horizontaler Ast angenommen wurde oder für eine Berechnung auf der "sicheren Seite", kann der Wert in den Stammdaten verändert oder eine separate Stahlsorte definiert werden.

Ansteigender ast.PNG


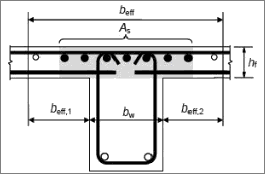
Ausgelagert.PNG
Hinweis:

Das MB-Baustatikmodul S340.de verteilt die ermittelte Zugbewehrung im Bereich negativer Momente ausschließlich im Stegbereich. Dies ist allerdings nicht zu empfehlen, da diese hohe Bewehrungskonzentration im Stegbereich, zu breiten Rissen in der Platte führt. Es wird daher im Eurocode 2 empfohlen, ca. 50% der Zugbewehrung in diesen Bereichen, auf die Hälfte der rechnerischen Gurtbreite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{eff,i}} zu verteilen. Eine solche Bewehrungsverteilung führt zu einem günstigeren Rissbild und einem besseren Tragverhalten des Bauteils.[2] [3]






Quellen

  1. ↑ Schneider Bautabellen für Ingenieure, 20. Auflage, Köln: Werner Verlag, 2012
  2. ↑ DIN EN 1992-1-1: Bemessung und Konstruktion von Stahlbeton und Spannbetontragwerken, Berlin: Beuth, 2010-2012
  3. ↑ Deutscher Ausschuss für Stahlbeton, Heft 600, Erläuterungen zu DIN EN 1992-1-1 und DIN EN 1992-1-1/NA (Eurocode), Berlin, 2012
Seiteninfo
Quality-flag-white.gif
Status: in Bearbeitung
Modul-Version: 2016.0500
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Nachweisführung_und_Bewehrungsermittlung_vergleichend_zur_MB-Baustatik_(Ermittlung_der_Biegezugbewehrung)&oldid=7138“