Durchstanzen - Korrekturfaktor β: Unterschied zwischen den Versionen
K (TSteffens verschob die Seite Durchstanzen (Korrekturfaktor β) nach Durchstanzen - Korrekturfaktor β, ohne dabei eine Weiterleitung anzulegen) |
|||
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | == | + | ==Definition== |
| − | + | ||
| − | + | Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der ''Lasterhöhungsfaktor β'' nach <ref>DIN EN 1992-1-1 (2011-01): Bemessung und Konstruktion von Stahlbeton- und Spannbetonbauwerken, Allgemeine Bemessungsregeln und Regeln für den Hochbau, 6.4.3</ref> berücksichtigt damit diesen Einfluss aus der nicht-rotationssymmetrischen Spannungsverteilung. | |
| − | Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der | + | Zur Ermittlung des Faktors β stehen nach DIN EN 1992-1-1 insgesamt 6 Verfahren zur Verfügung. <br /> |
| − | Zur Ermittlung des Faktors β stehen | + | Drei dieser Verfahren werden im Folgenden erläutert. |
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | === | + | ===Konstante Faktoren für ausgesteifte Systeme mit nahezu gleichen Stützweiten=== |
| − | + | ||
| − | + | Die nachfolgend angegebenen Faktoren gelten für horizontal unverschiebliche, ausgesteifte Systeme mit Stützweitenunterschieden von maximal 25 % und einer Belastung ausschließlich durch Gleichlasten <ref>DIN EN 1992-1-1 (2011-01): Bemessung und Konstruktion von Stahlbeton- und Spannbetonbauwerken, Allgemeine Bemessungsregeln und Regeln für den Hochbau, 6.4.3 (6)</ref>. Die Stützweitenverhältnisse betragen somit <math> 0,8 \leq l_1 / l_2 \leq 1,25 </math>. | |
| − | von maximal 25 % und | ||
| − | |||
[[Datei:Durchstanzen_10.png|300px|thumb|right| Korrekturfaktor Beta ]] | [[Datei:Durchstanzen_10.png|300px|thumb|right| Korrekturfaktor Beta ]] | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Für diesen Fall können | + | Für diesen Fall können folgende ''konstante Näherungswerte'' angenommen werden(siehe Bild 10): |
<br /> | <br /> | ||
| − | *1,10 Innenstützen | + | *1,10 - für Innenstützen |
| − | *1,40 Randstützen | + | *1,40 - für Randstützen |
| − | *1,35 Wandenden (NA) | + | *1,35 - für Wandenden (NA) |
| − | *1,50 Eckstützen | + | *1,50 - für Eckstützen |
| − | *1,20 Wandecken (NA) | + | *1,20 - für Wandecken (NA) |
| − | |||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 38: | Zeile 28: | ||
===Ermittlung über Sektormodell=== | ===Ermittlung über Sektormodell=== | ||
<br /> | <br /> | ||
| + | [[Datei:Durchstanzen_11.png|350px|thumb|right|Sektormodell ]] | ||
Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt | Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt | ||
oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung | oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung | ||
der Lasteinzugsfläche <math>A_{LE}</math> in i-Lasteinleitungssektoren <math>A_i</math> (siehe Bild) statt. | der Lasteinzugsfläche <math>A_{LE}</math> in i-Lasteinleitungssektoren <math>A_i</math> (siehe Bild) statt. | ||
| − | + | Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden <ref name="Q1" >K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, 2. Aufl. edition, 2016</ref>.<br />.<br /> | |
| − | Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden <ref name="Q1" >K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, | + | Der Lasterhöhungsfaktor ergibt sich somit wie folgt <ref name = "Q1"/>: |
| − | Der Lasterhöhungsfaktor ergibt sich somit wie folgt <ref name=" | ||
| − | |||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| + | |||
| + | :<math> V_{Ed}=e_d \cdot A_{LE}</math> | ||
| + | |||
| + | :<math> \nu_{Ed,m}=V_{Ed} / u_{crit}</math> | ||
| + | |||
:<math> \nu_{Ed,i}=e_d \cdot \frac{A_i}{u_i}</math> | :<math> \nu_{Ed,i}=e_d \cdot \frac{A_i}{u_i}</math> | ||
| − | + | ||
:<math> \beta=max\{ \nu_{Ed,i}/\nu_{Ed,m}\}</math> | :<math> \beta=max\{ \nu_{Ed,i}/\nu_{Ed,m}\}</math> | ||
| − | <br /> | + | |
| + | wobei: | ||
| + | :{| | ||
| + | |- | ||
| + | | e<sub>d</sub>… || Flächenbelastung innerhalb der Lasteinzugsfläche | ||
| + | |- | ||
| + | | A<sub>LE</sub>… || durch Lastscheiden begrenzte Lasteinzugsfläche | ||
| + | |}<br /> | ||
| + | |||
<br /> | <br /> | ||
| Zeile 66: | Zeile 65: | ||
Die Gleichung lautet somit wie folgt: | Die Gleichung lautet somit wie folgt: | ||
<br /> | <br /> | ||
| − | :<math>\beta=1+k\cdot\frac{M_{Ed}}{V_{Ed}}\cdot\frac{u_1}{W_1}\ | + | :<math>\beta=1+k\cdot\frac{M_{Ed}}{V_{Ed}}\cdot\frac{u_1}{W_1}\ge 1,10</math><br /> |
mit<br /> | mit<br /> | ||
<br /> | <br /> | ||
| Zeile 84: | Zeile 83: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA)<ref name = " | + | Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA)<ref name = "Q1"/>:<br /> |
<br /> | <br /> | ||
:<math>W_1=1+\sqrt{(k_y\cdot\frac{M_{Ed,y}}{V_{Ed}}\cdot\frac{u_1}{W_{1,y}})^2+(k_z\cdot\frac{M_{Ed,z}}{V_{Ed}}\cdot\frac{u_1}{W_{1,z}})^2}\ge 1,10</math> | :<math>W_1=1+\sqrt{(k_y\cdot\frac{M_{Ed,y}}{V_{Ed}}\cdot\frac{u_1}{W_{1,y}})^2+(k_z\cdot\frac{M_{Ed,z}}{V_{Ed}}\cdot\frac{u_1}{W_{1,z}})^2}\ge 1,10</math> | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
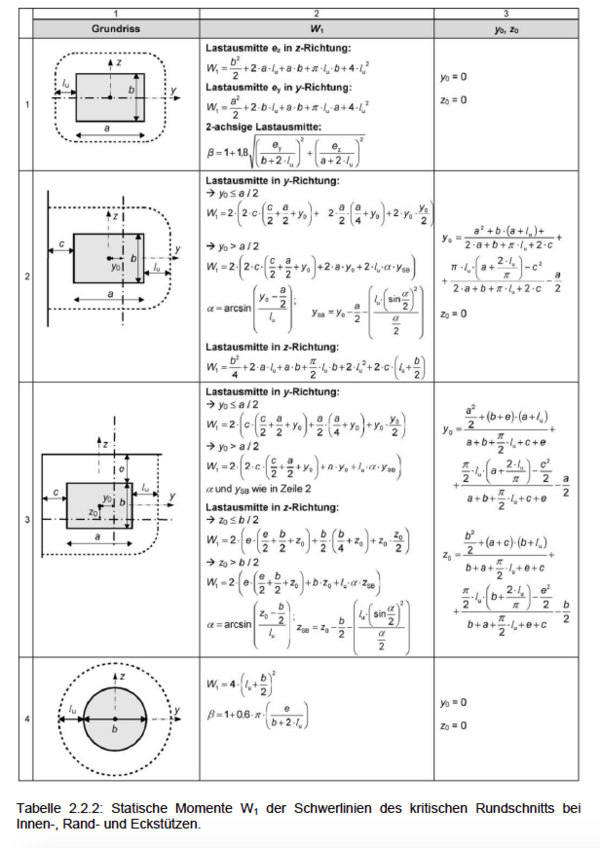
| − | [[Datei:Durchstanzen_(Korrekturfaktor_Beta)_5.png|600px|thumb|left|Tabelle Widerstandsmoment<ref name = " | + | [[Datei:Durchstanzen_(Korrekturfaktor_Beta)_5.png|600px|thumb|left|Tabelle Widerstandsmoment<ref name = "Q1"/>]]<br /> |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 142: | Zeile 141: | ||
==Quellen== | ==Quellen== | ||
<references /> | <references /> | ||
| − | |||
| − | |||
| − | {{Seiteninfo | + | {{Seiteninfo |
|Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | |Quality-flag = [[File:quality-flag-orange.gif|right|70px]] | ||
| − | |Status = Seite fertig, ungeprüft| | + | |Status = Seite fertig, ungeprüft|}} |
| − | + | [[Kategorie:Grundlagen/Begriffe-Stahlbetonbau]] | |
Aktuelle Version vom 10. April 2024, 15:24 Uhr
Definition
Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der Lasterhöhungsfaktor β nach [1] berücksichtigt damit diesen Einfluss aus der nicht-rotationssymmetrischen Spannungsverteilung.
Zur Ermittlung des Faktors β stehen nach DIN EN 1992-1-1 insgesamt 6 Verfahren zur Verfügung.
Drei dieser Verfahren werden im Folgenden erläutert.
Konstante Faktoren für ausgesteifte Systeme mit nahezu gleichen Stützweiten
Die nachfolgend angegebenen Faktoren gelten für horizontal unverschiebliche, ausgesteifte Systeme mit Stützweitenunterschieden von maximal 25 % und einer Belastung ausschließlich durch Gleichlasten [2]. Die Stützweitenverhältnisse betragen somit .
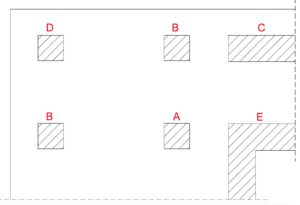
Für diesen Fall können folgende konstante Näherungswerte angenommen werden(siehe Bild 10):
- 1,10 - für Innenstützen
- 1,40 - für Randstützen
- 1,35 - für Wandenden (NA)
- 1,50 - für Eckstützen
- 1,20 - für Wandecken (NA)
Ermittlung über Sektormodell
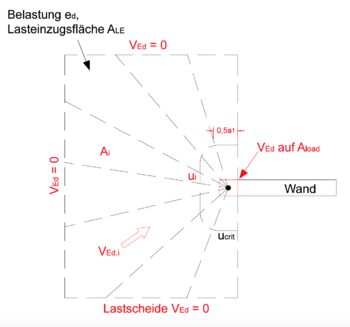
Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt
oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung
der Lasteinzugsfläche in i-Lasteinleitungssektoren (siehe Bild) statt.
Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden [3].
.
Der Lasterhöhungsfaktor ergibt sich somit wie folgt [3]:
wobei:
ed… Flächenbelastung innerhalb der Lasteinzugsfläche ALE… durch Lastscheiden begrenzte Lasteinzugsfläche
Genaueres Verfahren
nach EC 2-1-1, 6.4.3 (1;2)
Sind die oben genannten Voraussetzungen nicht erfüllt oder ist die bezogene Ausmitte bei Randstützen größer als 1,2 (wobei c die Stützenabmessung in Richtung der Ausmitte darstellt), ist der Lasterhöhungsfaktor mit genaueren Verfahren
zu ermitteln. Hierbei wird die Annahme einer vollplastischen Schubspannungsverteilung am kritischen Rundschnitt getroffen [4].
Die Gleichung lautet somit wie folgt:
mit
und somit bei einer geschlossenen Rechteckstütze mit c1 parallel und c2 senkrecht zur Lastausmitte:
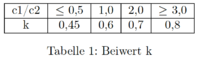
und dem Beiwert k
Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA)[3]:
Quellen
- ↑ DIN EN 1992-1-1 (2011-01): Bemessung und Konstruktion von Stahlbeton- und Spannbetonbauwerken, Allgemeine Bemessungsregeln und Regeln für den Hochbau, 6.4.3
- ↑ DIN EN 1992-1-1 (2011-01): Bemessung und Konstruktion von Stahlbeton- und Spannbetonbauwerken, Allgemeine Bemessungsregeln und Regeln für den Hochbau, 6.4.3 (6)
- ↑ 3,0 3,1 3,2 3,3 K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, 2. Aufl. edition, 2016
- ↑ Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
Seiteninfo
|