Betondeckung (Bsp.)

Beispiel 1 Stahlbetonträger im Außenbereich

Das folgende Beispiel zeigt eine Berechnung der Betondeckung, wie Sie mit dem Modul S340.de geführt wird.

Aufgabe

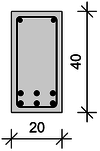
Ermittlung der Betondeckung sowie der statischen Nutzhöhe, für einen Stahlbetonträger im Außenbereich mit direkter Bewetterung:

Vorgabewerte

Beton: C 25/30 (XC4)
untere Längsbewehrung: 2 Lagen je 3ø16
obere Längsbewehrung: 2ø12
Bügelbewehrung: ø8

Berechnung

Mindestbetondeckung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_\mathrm{min}=\mathrm{max}\begin{cases} c_\mathrm{min,b} \\ c_\mathrm{min,dur} + \Delta c_\mathrm{dur,\lambda} - \Delta c_\mathrm{dur,st} - \Delta c_\mathrm{dur,add} \\ 10\,\mathrm{mm} \end{cases}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_\mathrm{min}=\mathrm{max}\begin{cases} c_\mathrm{min,b} &= 16\,\mathrm{mm} \\ 25\,\mathrm{mm} + 0\,\mathrm{mm} - 0\,\mathrm{mm} - 0\,\mathrm{mm} &= \underline{25\,\mathrm{mm}}~~~\mathrm{(Korrosionsschutz~massg.)} \\ 10\,\mathrm{mm} &= 10\,\mathrm{mm} \end{cases}}

Vorhaltemaß

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta c_\mathrm{dev}=\underline{15\,\mathrm{mm}}}

Nennmaß vom Bügel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_\mathrm{nom,bue}=c_\mathrm{min} + \Delta c_\mathrm{dev} =25\,\mathrm{mm} + 15\,\mathrm{mm}=\underline{40\,\mathrm{mm}}}

Abstand der Schwerachse der Biegezugbewehrung zum Rand der Bewehrung

untere Längsbewehrung (zweilagig)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{e}=\cfrac{\sum_{i} A_\mathrm{S,i} \cdot \mathrm{e_{i}}}{\sum_{i} A_\mathrm{S,i}}=\cfrac{3 \cdot 201\,\mathrm{mm}^{2} \cdot 44\,\mathrm{mm} + 3 \cdot 201\,\mathrm{mm}^{2} \cdot 8\,\mathrm{mm}}{6 \cdot 201\,\mathrm{mm}^{2}}=\underline{26\,\mathrm{mm}}}

obere Längsbewehrung (einlagig)

$\mathrm {e} =0{,}5\cdot \mathrm {\emptyset _{l}} =0{,}5\cdot 12\,\mathrm {mm} ={\underline {6\,\mathrm {mm} }}$

statische Nutzhöhe

untere Längsbewehrung (zweilagig)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d=h - c_\mathrm{nom} - \mathrm{\O_{Bue}} - \mathrm{e}=400\,\mathrm{mm} - 40\,\mathrm{mm} - 8\,\mathrm{mm} - 26\,\mathrm{mm}=\underline{\underline{326\,\mathrm{mm}}}}

damit ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d'_\mathrm{u}=\underline{\underline{74\,\mathrm{mm}}}}

obere Längsbewehrung (einlagig)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d=h - c_\mathrm{nom} - \mathrm{\O_{Bue}} - \mathrm{e}=400\,\mathrm{mm} - 40\,\mathrm{mm} - 8\,\mathrm{mm} - 6\,\mathrm{mm}=\underline{\underline{346\,\mathrm{mm}}}}

damit ergibt sich:

$d'_{\mathrm {u} }={\underline {\underline {54\,\mathrm {mm} }}}$

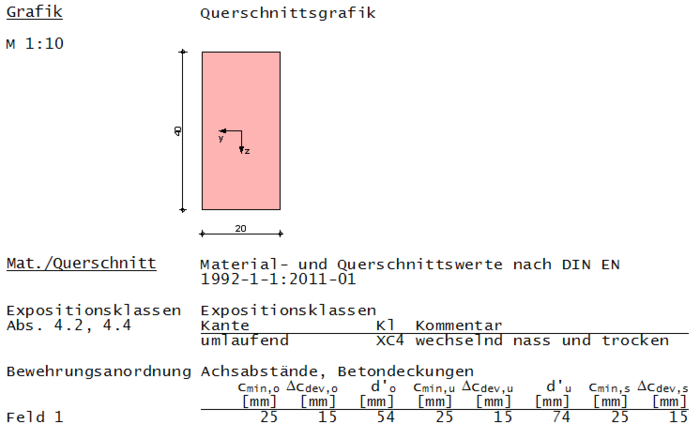
Vergleich mit mb-AEC Baustatik

Bei Eingabe der oben vorgegebenen Werte, erscheint folgender Ausdruck:

Sonstiges

• Modul-Version: 2014.011
• Autor: R. Wengatz
• Veröffentlicht am: 24.02.2015
• Status: in Bearbeitung