Bemessung eines Randstreifenfundaments (Bsp.): Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| Zeile 49: | Zeile 49: | ||
;Gesuchte Größen | ;Gesuchte Größen | ||
<br /> | <br /> | ||
| − | :<math>\sigma_{2} = \frac{\frac{2}{3} \cdot b^{2} - c \cdot b + \delta + \alpha}{\frac{b^{2}}{6} + \delta + \alpha} \cdot \gamma = \frac{\frac{2}{3} \cdot 50,0^{2} - 15,0 \cdot 50,0 + 701,18 + 11739,13}{\frac{50,0^{2}}{6} + 701,18 + 11739,13} \cdot 0,014796 = 0,015659 kN/cm^{2}</math> | + | :<math>\sigma_{2} = \frac{\frac{2}{3} \cdot b^{2} - c \cdot b + \delta + \alpha}{\frac{b^{2}}{6} + \delta + \alpha} \cdot \gamma = \frac{\frac{2}{3} \cdot 50,0^{2} - 15,0 \cdot 50,0 + 701,18 + 11739,13}{\frac{50,0^{2}}{6} + 701,18 + 11739,13} \cdot 0,014796 = 0,015659\ kN/cm^{2} \underline{\underline{= 156,59\ kN/m^{2}}}</math> |
| + | <br /> | ||
| + | :<math>\sigma_{1} = 2 \cdot \gamma - \sigma_{2} = 2 \cdot 0,014796 - 0,015659 = 0,013933\ kN/cm^{2}\underline{\underline{= 139,33\ kN/m^{2}}}</math> | ||
| + | <br /> | ||
| + | :<math>M_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \alpha = \left( 0,015659 - 0,014796 \right) \cdot 11739,13 = 10,13\ kNcm/cm \underline{\underline{= 10,13\ kNm/m}}</math> | ||
| + | <br /> | ||
| + | :<math>H_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \frac{\delta}{\beta} = \left( 0,015659 - 0,014796 \right) \cdot \frac{701,18}{32,5} = 0,0186 kN/cm \underline{\underline{= 1,86\ kN/m}}</math> | ||
| + | <br /> | ||
| + | Die Sohldruckresultierende liegt im Schwerpunkt des Spannungstrapezes | ||
| + | ==mb-Worksuite Vergleichsrechnung== | ||
| − | |||
==Quellen== | ==Quellen== | ||
<references /> | <references /> | ||
Version vom 29. Juni 2021, 14:26 Uhr
Folgend soll ein Berechnungsbeispiel für ein Randstreifenfundament nach dem Kanya-Verfahren[1] gezeigt werden. Anschließend wird das Ergebnis der Handrechnung mit der Ergebnisausgabe des mb-Worksuite Moduls S501.de verglichen.
Aufgabenstellung
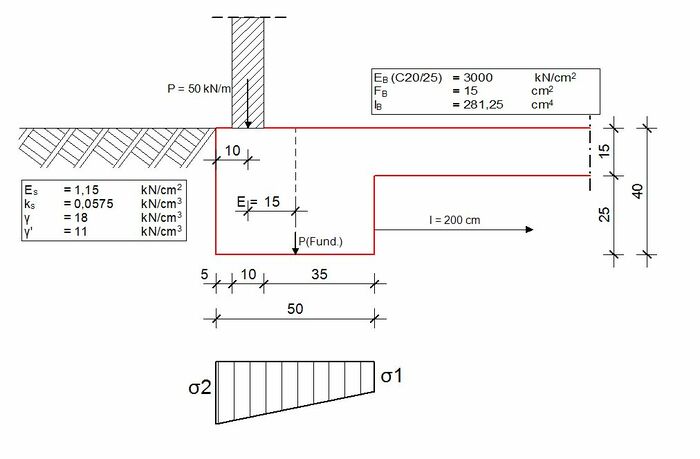
Ein Randstreifenfundament mit den folgenden Eigenschaften soll mit dem "vereinfachten Nachweis in Regelfällen" nach DIN 1054[2] nachgewiesen werden.
| Formelzeichen | Wert | Einheit |
|---|---|---|
| a | 40,0 | cm |
| b | 50,0 | cm |
| c | 15,0 | cm |
| l | 200 | cm |
| EB(C20/25) | 3000 | kN/cm2 |
| Es | 1,15 | kN/cm2 |
| P | 0,50 | kN/cm |
| PEd | 0,675 | kN/cm |
| PFund. | 0,048 | kN/cm |
| PEd (inkl. PFund. | 0,7398 | kN/cm |
| FB | 15,0 | cm2 |
| IB | 281,25 | cm4 |
| E | 15 | cm |
Handrechnung
- Vorwerte
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha = 3,2 \cdot \frac{E_{B} \cdot I_{B}}{l \cdot E_{S}} = 3,2 \cdot \frac{3000,0 \cdot 281,25}{200 \cdot 1,15} = 11739,13}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta = a - \frac{d}{2} = 40,0 - \frac{15,0}{2} = 32,5}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma = \frac{P}{b} = \frac{0,7398}{50,0} = 0,014796}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta = \frac{2 \cdot \beta^{2}}{3 \cdot F_{B} \cdot E_{B} + 2,5 \cdot l \cdot E_{S}} \cdot F_{B} \cdot E_{B} = \frac{2 \cdot 32,5_{2}}{3 \cdot 15,0 \cdot 3000,0 + 2,5 \cdot 200 \cdot 1,15} \cdot 15,0 \cdot 3000,0 = 701,18}
- Gesuchte Größen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{2} = \frac{\frac{2}{3} \cdot b^{2} - c \cdot b + \delta + \alpha}{\frac{b^{2}}{6} + \delta + \alpha} \cdot \gamma = \frac{\frac{2}{3} \cdot 50,0^{2} - 15,0 \cdot 50,0 + 701,18 + 11739,13}{\frac{50,0^{2}}{6} + 701,18 + 11739,13} \cdot 0,014796 = 0,015659\ kN/cm^{2} \underline{\underline{= 156,59\ kN/m^{2}}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \alpha = \left( 0,015659 - 0,014796 \right) \cdot 11739,13 = 10,13\ kNcm/cm \underline{\underline{= 10,13\ kNm/m}}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_{Z} = \left( \sigma_{2} - \gamma \right) \cdot \frac{\delta}{\beta} = \left( 0,015659 - 0,014796 \right) \cdot \frac{701,18}{32,5} = 0,0186 kN/cm \underline{\underline{= 1,86\ kN/m}}}
Die Sohldruckresultierende liegt im Schwerpunkt des Spannungstrapezes
mb-Worksuite Vergleichsrechnung
Quellen
- ↑ J. Kanya, „Berechnung ausmittig belasteter Streifenfundamente mit Zentrierung durch eine Stahlbeton-Fußbodenplatte,“ Die Bautechnik, pp. 154-159, Mai 1969
- ↑ DIN e.V., Hrsg., „A 6.10 Vereinfachter Nachweis in Regelfällen,“ in DIN 1054:2015-11, Baugrund-Sicherheitsnachweise im Erd und Grundbau-Ergänzende Regelungen zu DIN EN 1997-1, Berlin, Beuth Verlag, 2015, pp. 47-56
Seiteninfo
|