Lasteinzugsfläche (Bsp.)

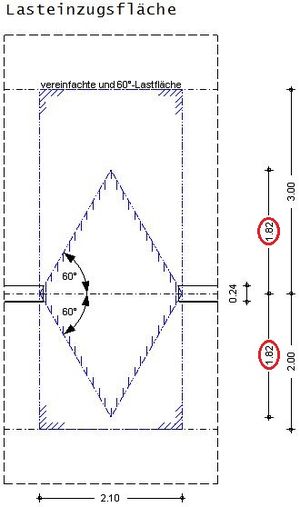
Beispiel 1

Aufgabe

Ermittlung der Lasteinzugsfläche eines deckengleichen Unterzuges anhand folgender Ausgangswerte.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{eff}=2,1m\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{P,o}=6,0m\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{P,u}=4,0m\end{align}}

Berechnung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{E}=\cfrac{l_\mathrm{eff}}{2}*tan(60)=\cfrac{2,1m}{2}*tan(60)=\underline{\underline{1,82\,\mathrm{m}}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eo}=\cfrac{l_\mathrm{P,o}}{2}=\cfrac{6,0m}{2}=\underline{\underline{3,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eu}=\cfrac{l_\mathrm{P,u}}{2}=\cfrac{4,0m}{2}=\underline{\underline{2,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}

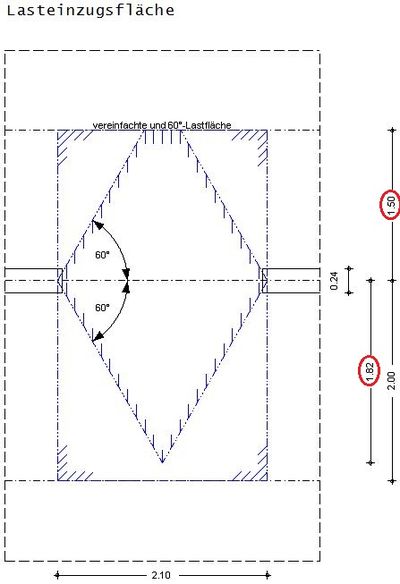
Beispiel 2

Aufgabe

Ermittlung der Lasteinzugsfläche eines deckengleichen Unterzuges anhand folgender Ausgangswerte.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{eff}=2,1m\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{P,o}=3,0m\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{P,u}=4,0m\end{align}}

Berechnung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{E}=\cfrac{l_\mathrm{eff}}{2}*tan(60)=\cfrac{2,1m}{2}*tan(60)=\underline{\underline{1,82\,\mathrm{m}}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eo}=\cfrac{l_\mathrm{P,o}}{2}=\cfrac{3,0m}{2}=\underline{\underline{1,5\,\mathrm{m}}}<1,82m~(l_\mathrm{Eo}~ist~massgebend)}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eu}=\cfrac{l_\mathrm{P,u}}{2}=\cfrac{4,0m}{2}=\underline{\underline{2,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}

Sonstiges

• Modul-Version: 2015.0240
• Autor: T. Lange
• Veröffentlicht am: 14.04.2015
• Status: in Bearbeitung