Brandschutznachweis Stahlbetonstütze (Bsp.): Unterschied zwischen den Versionen
| Zeile 86: | Zeile 86: | ||
| <math>{\alpha_{cc}}= 0,85 || Dauerstandfestigkeit nach DIN EN 1992-1-1 | | <math>{\alpha_{cc}}= 0,85 || Dauerstandfestigkeit nach DIN EN 1992-1-1 | ||
|- | |- | ||
| − | | <math>{\omega}=\frac{{{A}_{s}\cdot{f}_{yd}}}{{{A}_{c}\cdot{f}_{cd}}}</math> | + | | <math>{\omega}=\frac{{{A}_{s}\cdot {f}_{yd}}}{{{A}_{c}\cdot{f}_{cd}}}</math> || mechanischer Bewehrungsgrad |
|} | |} | ||
Version vom 26. Juli 2023, 14:46 Uhr
Ein Beispiel für die Berechnung einer Stahlbeton-Innenstütze mit der Methode A des vereinfachten Verfahrens
Aufgabenstellung
Gegeben
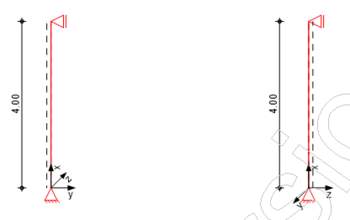
- eine Stahlbeton-Innenstütze in einem ausgesteiften Bauwerk
- Kopf und Fuß der Stütze sind rotationsbehindert (eingespannt)
- l = 4m
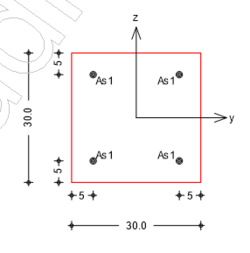
- h/b = 300/300
- NEd = 400kN
- vorhandene Bewehrung: 4Ø12 Längsbewehrung; Ø8 Bügelbewehrung alle 14 cm; As,vorh = 4,52 cm2
Gefordert
Für die Stahlbeton-Innenstütze wird eine Feuerwiderstandsdauer für 60 Minuten unter einer mehrseitigen Brandbeanspruchung gefordert.
Nachweis mit der Tabelle 5.2a der Methode A
Randbedingungen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0,fi}} \leq 3m}
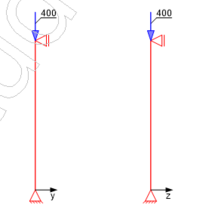
Da der Kopf und der Fuß der Stütze rotationsbehindert gelagert sind, ergibt sich die Knicklänge für den Brandfall für eine Innenstütze mit: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0,fi}} = 0,5 \cdot l = 0,5 \cdot 4m = 2m} Die Randbedingung ist mit 2m ≤ 3m erfüllt.
- Bewehrungsgehalt ρ
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho = \frac{{{4,52 cm^2}}}{{{30 cm \cdot 30 cm}}} = 0,5 % \leq 4 %}
- Die Randbedingung ist erfüllt.
Schnittgrößen
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Rd}} \approx {{N }_{ED}} = -400 kN}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{fi}} =\frac{{{N}_{Ed,fi,t}}}{{{N}_{Rd}}} = \frac{{{-280 kN}}}{{{-400 kN}}} = 0,7}
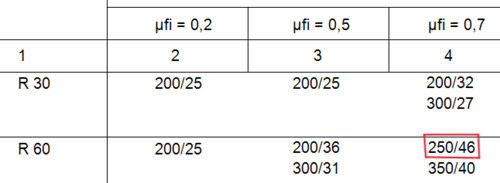
erforderliche Querschnittsabmessungen nach der Tabelle 5.2a
bmin = 250mm aerf = 46mm
vorhandene Querschnittsabmessungen
b = 300mm a = 50mm
- Die Stahlbeton-Innenstütze kann der Feuerwiderstandsklasse R60 zugeordnet werden.
vergleichende Berechnung mit mB Baustatik
Nachweis mit der Gleichung 5.7 der Methode A
Randbedingungen
- Achsabstand a: 25mm ≤ a ≤ 80mm → a = 50mm, Randbedingung erfüllt.
- Stützenlänge: l0,fi ≤ 6m → l0,fi = 2m, Randbedingung erfüllt.
- h ≤ 1,5*b → 300mm ≤ 1,5*300mm → 300mm ≤ 450mm, Randbedingung erfüllt.
- 200mm ≤ b` ≤ 450mm → 200mm ≤ (2*Ac)/(b+h) ≤ 450mm → 200mm ≤ (2*3002)/(300+300) ≤ 450mm → 200mm ≤ 300mm ≤ 450mm, Randbedingung erfüllt.
Gleichung 5.7
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=120\cdot {{\left( \frac{{{R}_{\eta fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}}
Ermittlung der Einflussfaktoren
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\eta_{fi}}= 0,7 || Ausnutzungsgrad |- | <math> n = 4 || Anzahl der Bewehrungsstäbe |- | <math>{\alpha_{cc}}= 0,85 || Dauerstandfestigkeit nach DIN EN 1992-1-1 |- | <math>{\omega}=\frac{{{A}_{s}\cdot {f}_{yd}}}{{{A}_{c}\cdot{f}_{cd}}}} mechanischer Bewehrungsgrad
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {R_{a}}=1,6\cdot (a-30)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {R_{l}}=9,6\cdot (5-{{l}_{0,fi}})}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {R_{b}}=0,09\cdot b'}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {R_{n}}=0\quad f\ddot{u}r\quad n=4 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {R_{n}}=12\quad f\ddot{u}r\quad n>4 }
Ergebnis der Berechnung
Quellen
Seiteninfo
|