Schnittgrößenermittlung deckengleicher Unterzug (Bsp.)

Aufgabe

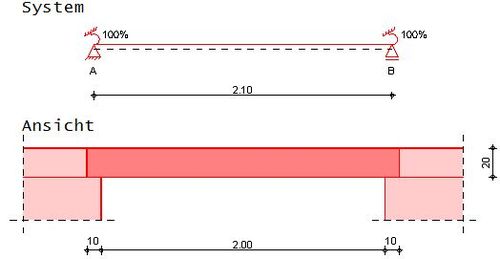
Ermittlung der Schnittgrößen für die Bemessung eines deckengleichen Unterzuges am Zwischenauflager anhand folgender Ausgangssituation:

Maße

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Deckendicke~h = 0,20m}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Wanddicke~t = 0,24m}

$Lichte~Stuetzweite~l_{\mathrm {n} }=2,00m$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Plattenstuetzweite~l_\mathrm{P,o} = 6,00m}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Plattenstuetzweite~l_\mathrm{P,u} = 4,00m}

Baustoffe

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Beton~C25/30~(XC1)~mit~f_\mathrm{ck} =25 N/mm^2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Betonstahl~Bst~500~S~(A)~mit~f_\mathrm{yk} =500 N/mm^2}

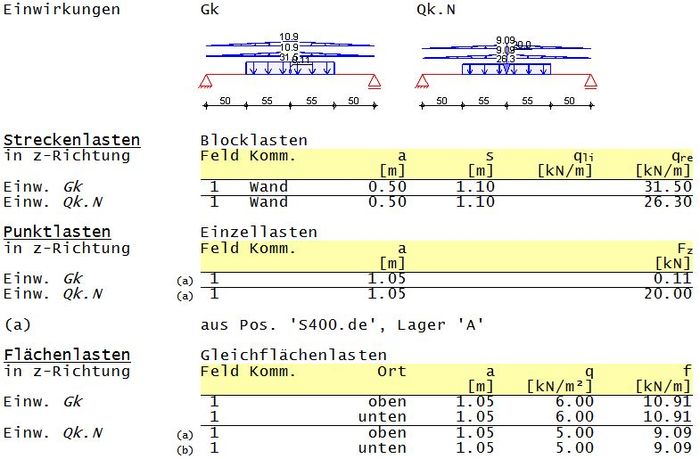
Einwirkungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Eigengewicht~der~Decke~g_\mathrm{k} = 6,00kN/m^2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Verkehrslast~der~Decke~q_\mathrm{k} = 5,00kN/m^2}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Stuetze~aus~uebernommener~Pos.~(mittig)~N_\mathrm{G} = 0,11kN}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Stuetze~aus~uebernommener~Pos.~(mittig)~N_\mathrm{Q} = 20,00kN}

$Blocklast~f_{\mathrm {gk} }=31,50kN/m$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Blocklast~f_\mathrm{qk} = 26,30kN/m}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Abstand~der~Blocklast~vom~linken~Auflager~a = 0,50m}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Laenge~der~Blocklast~s = 1,10m}

Sicherheitsbeiwerte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}\gamma_\mathrm{G} =1,35\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}\gamma_\mathrm{Q} =1,50\end{align}}

Berechnung

Effektive Stützweite

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{eff} = l_\mathrm{n}*1,05 = 2,00m*1,05 = \underline{2,10\,\mathrm{m}}\end{align}}

Anwendung der Theorie des deckengleichen Unterzuges möglich?

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cfrac{l}{h} = \cfrac{2,10m}{0,20m} = \underline{10,5}}

$7\leq 10,5\leq 15$

(Unterbrochene Stützung mit mäßiger Länge)

Achtung:

• Das Modul berechnet die Biegeschlankheit mit l_n, was aber nicht den Vorgaben des DAfstb Heft 240 entspricht!

Lasteinzugsfläche

siehe Lasteinzugsfläche (Bsp.)

Mitwirkende Plattenbreiten (Zwischenauflager)

siehe Mitwirkende Plattenbreite deckengleicher Unterzug (Bsp.)

Flächenlasten

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{Gk} = g_\mathrm{k} * b_\mathrm{E} = 6,00kN/m^2 * 1,82m = \underline{10,91kN/m}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_\mathrm{Qk} = q_\mathrm{k} * b_\mathrm{E} = 5,00kN/m^2 * 1,82m = \underline{9,09kN/m}}

Charakteristische Schnittgrößen

Hinweis:

• Das Modul berechnet die charakteristischen Schnittgrößen für sich und summiert sie am Ende auf. Die Bemessungsschnittgrößen werden aus den Endergebnissen mittels Kombination ermittelt.
• Einzellasten sind in der Grafik oft schlecht zu erkennen.

Ständige Lasten:

• Eigengewicht der Decke (Schneider 21. Auflager S. 4.11)
  
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,k} = \cfrac{q*l}{2} = \cfrac{0,912kN/m * 2,10m}{2} = \underline{11,46kN}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -(1+\beta+\beta^2-1,5*\beta^3)*\cfrac{q*l}{30}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -(1+0,5+0,5^2-1,5*0,5^3) * \cfrac{2*6,00kN/m² * (2,10m)^2}{30} = \underline{-5,01kNm}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = -M_\mathrm{A} + \cfrac{l}{2} * V_\mathrm{A} - \cfrac{l}{2} * \cfrac{l}{6} * q}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = 5,01kNm + \cfrac{2,10m}{2} * 11,46kN - \cfrac{2,10m}{2} * \cfrac{2,10m}{6} * 6,00kN/m^2 = \underline{3,01 kNm}}

• Eigengewicht der Stütze (Schneider 21. Auflager S. 4.8)
  
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,k} = \cfrac{F}{2} = \cfrac{0,11 kN}{2} = \underline{0,055 kN}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -\cfrac{F*l}{8} = -\cfrac{0,11 kN* 2,10m}{8} = \underline{-0,03kNm}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = \cfrac{F*l}{8} = \cfrac{0,11 kN* 2,10m}{8} = \underline{0,03kNm}}

• Ständige Last der Blocklast (Schneider 21. Auflager S. 4.11)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,k} = [\epsilon+(\epsilon-\delta)(\delta*\epsilon-\cfrac{\gamma^2}{4})]*F}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,k} = [0,5+0]*34,65kN = \underline{17,33kN}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -[\delta*\epsilon^2+(\cfrac{1}{3}-\epsilon)*\cfrac{\gamma^2}{4}]*F*l}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -[0,5*0,5^2+(\cfrac{1}{3}-0,5)*\cfrac{0,524^2}{4}]*34,65kN * 2,10m = \underline{-8,26kNm}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = M_\mathrm{A} + \cfrac{l}{2} * V_\mathrm{A} - \cfrac{s}{2} * \cfrac{s}{4} * 31,50kN/m}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = -8,26kNm + \cfrac{2,10m}{2} * 17,44kN - \cfrac{1,10m}{2} * \cfrac{1,10m}{4} * 31,50kN/m = \underline{5,16kNm}}

• Summe der charakteristischen Schnittgrößen
  
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,k} = 11,46kN + 0,055kN + 17,33kN = \underline{\underline{28,84kN}}}

$V_{\mathrm {B,k} }={\underline {\underline {-28,84kN}}}$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = -5,01kNm - 0,03kNm - 8,26kNm = \underline{\underline{-13,30kNm}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{B,k} = \underline{\underline{-13,30kNm}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,k} = 3,01 kNm + = 0,03kNm + 5,16kNm = \underline{\underline{8,20kNm}}}

Veränderliche Lasten:

(Werden analog zu den ständigen Lasten ermittelt)

$V_{\mathrm {A,k} }={\underline {\underline {34,01kN}}}$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{B,k} = \underline{\underline{-34,01kN}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,k} = \underline{\underline{-16,33kNm}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{B,k} = \underline{\underline{-16,33kNm}}}

$M_{\mathrm {F,k} }={\underline {\underline {12,07kNm}}}$

Bemessungsschnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}E_\mathrm{d} = \gamma_\mathrm{G} * G_\mathrm{k} + \gamma_\mathrm{Q} * Q_\mathrm{k}\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{A,d} = 1,35 * 28,84kN + 1,5 * 34,01kN = \underline{\underline{89,95kN}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{B,d} = \underline{\underline{-89,95kN}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{A,d} = 1,35 * (-13,30) + 1,5 * (-16,33) = \underline{\underline{-42,45kNm}}}

$M_{\mathrm {B,d} }={\underline {\underline {-42,45kNm}}}$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{F,d} = 1,35 * 8,20kNm + 1,5 * 12,07kNm = \underline{\underline{29,17kNm}}}

Ausdruck in mb-AEC Baustatik

Sonstiges

• Modul-Version: 2015.0240
• Autor: T. Lange
• Veröffentlicht am: 18.04.2015
• Status: in Bearbeitung