Durchstanzen - Lasteinleitungsfläche und kritischer Rundschnitt: Unterschied zwischen den Versionen
Mwulf (Diskussion | Beiträge) |
Mwulf (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
==Lasteinleitungsfläche und kritischer Rundschnitt== | ==Lasteinleitungsfläche und kritischer Rundschnitt== | ||
<br /> | <br /> | ||
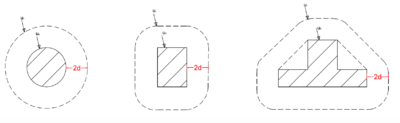
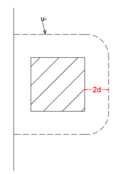
| − | [[Datei:Durchstanzen_4.png|400px|thumb|right| | + | [[Datei:Durchstanzen_4.png|400px|thumb|right|Kritischer Rundschnitt bei variablen Geometrien ]] |
Die Bemessung der '''Lasteinleitungsfläche A<sub>load</sub>''' mit dem kritischen Rundschnitt u<sub>1</sub> gilt für folgende Geometrien:<br /> | Die Bemessung der '''Lasteinleitungsfläche A<sub>load</sub>''' mit dem kritischen Rundschnitt u<sub>1</sub> gilt für folgende Geometrien:<br /> | ||
*Rundstützen mit dem Umfang <math>u_0 \leq 12d</math> | *Rundstützen mit dem Umfang <math>u_0 \leq 12d</math> | ||
| Zeile 12: | Zeile 12: | ||
<br /> | <br /> | ||
<math> \frac{(d_x+d_y)}{2}</math> | <math> \frac{(d_x+d_y)}{2}</math> | ||
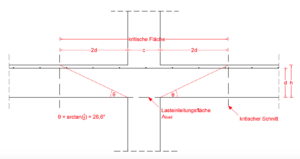
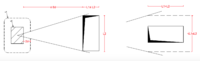
| − | [[Datei:Durchstanzen_5.png|300px|thumb|right| | + | [[Datei:Durchstanzen_5.png|300px|thumb|right|Bezeichnungen am kritischen Rundschnitt ]] |
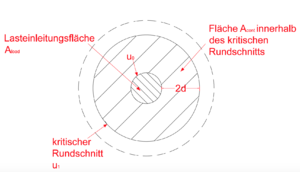
| − | [[Datei:Durchstanzen_6.png|300px|thumb|right| | + | [[Datei:Durchstanzen_6.png|300px|thumb|right|Draufsicht eines kritischen Rundschnitts]] |
<br /> | <br /> | ||
Die Lasteinleitungsfläche darf sich nicht in der Nähe von anderen konzentrierten Lasten sowie anderen wirkenden Querkräften befinden, was eine Überschneidung der kritischen Rundschnitte zur Folge hätte<ref name="Q1" >K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>.<br /> | Die Lasteinleitungsfläche darf sich nicht in der Nähe von anderen konzentrierten Lasten sowie anderen wirkenden Querkräften befinden, was eine Überschneidung der kritischen Rundschnitte zur Folge hätte<ref name="Q1" >K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012</ref>.<br /> | ||
| Zeile 19: | Zeile 19: | ||
Einwirkung und Widerstand werden auf den kritischen Rundschnitt bezogen, dieser wird bei Rund- und Rechteckstützen im Abstand 2d von der Lasteinleitungsfläche gebildet (siehe Bild 4) <ref name="Q5" >Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript</ref>. | Einwirkung und Widerstand werden auf den kritischen Rundschnitt bezogen, dieser wird bei Rund- und Rechteckstützen im Abstand 2d von der Lasteinleitungsfläche gebildet (siehe Bild 4) <ref name="Q5" >Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript</ref>. | ||
<br /> | <br /> | ||
| − | Die kritische Fläche A<sub>cont</sub> stellt die Fläche innerhalb des kritischen Rundschnitts u<sub>1</sub> dar (siehe | + | Die kritische Fläche A<sub>cont</sub> stellt die Fläche innerhalb des kritischen Rundschnitts u<sub>1</sub> dar (siehe Bilder) . |
<br /> | <br /> | ||
Bei der Ermittlung des kritischen Rundschnitts sind einspringende Ecken zu überlesen, da der kleinste aller Rundschnitte maßgebend ist <ref name="Q5" />. <br /> | Bei der Ermittlung des kritischen Rundschnitts sind einspringende Ecken zu überlesen, da der kleinste aller Rundschnitte maßgebend ist <ref name="Q5" />. <br /> | ||
| Zeile 34: | Zeile 34: | ||
===Ausgedehnte Einleitungsflächen=== | ===Ausgedehnte Einleitungsflächen=== | ||
<br /> | <br /> | ||
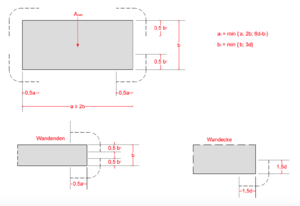
| − | [[Datei:Durchstanzen_7.png|300px|thumb|left| | + | [[Datei:Durchstanzen_7.png|300px|thumb|left|Kritischer Rundschnitt bei ausgedehnten Einbeitungsflächen ]] |
Ist das Seitenverhältnis <math>a/b > 2 </math> oder der Umfang der Lasteinleitungsfläche <math>A_{load} > 12d</math>, so müssen gesonderte Nachweise geführt werden, <br /> | Ist das Seitenverhältnis <math>a/b > 2 </math> oder der Umfang der Lasteinleitungsfläche <math>A_{load} > 12d</math>, so müssen gesonderte Nachweise geführt werden, <br /> | ||
| − | welche nur auf Teilrundschnitte mit <math>u_0 \ge 12d</math> zu beziehen sind (siehe Bild | + | welche nur auf Teilrundschnitte mit <math>u_0 \ge 12d</math> zu beziehen sind (siehe Bild).<br /> |
Der Querkraftwiderstand ist für alle weiteren, über den Umfang hinaus ragenden Bereiche zu ermitteln. <br /> | Der Querkraftwiderstand ist für alle weiteren, über den Umfang hinaus ragenden Bereiche zu ermitteln. <br /> | ||
Die Summe aus der Durchstanztragfähigkeit sowie der Querkrafttragfähigkeit bildet den Gesamtwiderstand <ref name="Q5" />. | Die Summe aus der Durchstanztragfähigkeit sowie der Querkrafttragfähigkeit bildet den Gesamtwiderstand <ref name="Q5" />. | ||
| Zeile 52: | Zeile 52: | ||
===Randnähe=== | ===Randnähe=== | ||
| − | [[Datei:Durchstanzen_8.png|120px|thumb|left| | + | [[Datei:Durchstanzen_8.png|120px|thumb|left|Kritischer Rundschnitt in Randnähe ]] |
<br /> | <br /> | ||
Liegt die Lasteinleitungsfläche nahe eines freien Randes, so ist der minimale kritische Rundschnitt möglicherweise nicht mehr geschlossen und endet in diesem Fall stets orthogonal zu diesem <ref name="Q5" />. <br /> | Liegt die Lasteinleitungsfläche nahe eines freien Randes, so ist der minimale kritische Rundschnitt möglicherweise nicht mehr geschlossen und endet in diesem Fall stets orthogonal zu diesem <ref name="Q5" />. <br /> | ||
| − | Im zutreffenden Fall ist der Rundschnitt wie | + | Im zutreffenden Fall ist der Rundschnitt wie im Bild aufgezeigt anzunehmen. |
Dieser Rundschnitt wird jedoch nur maßgebend, wenn der Umfang kleiner ist als der des "Regelrundschnitts" bei geschlossener Schnittführung <ref name= "Q8">G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010</ref>.<br /> | Dieser Rundschnitt wird jedoch nur maßgebend, wenn der Umfang kleiner ist als der des "Regelrundschnitts" bei geschlossener Schnittführung <ref name= "Q8">G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010</ref>.<br /> | ||
Beträgt der Abstand zum freien Rand < d, so ist in der Regel eine besondere Randbewehrung einzulegen <ref name="Q1" />. | Beträgt der Abstand zum freien Rand < d, so ist in der Regel eine besondere Randbewehrung einzulegen <ref name="Q1" />. | ||
| Zeile 70: | Zeile 70: | ||
===Öffnungen=== | ===Öffnungen=== | ||
| − | [[Datei:Durchstanzen_9.png|200px|thumb|left| | + | [[Datei:Durchstanzen_9.png|200px|thumb|left|Kritischer bei Öffnungen ]] |
<br /> | <br /> | ||
Liegt der Rand der Lasteinleitungsfläche im Abstand < 6d von einer Öffnung entfernt, so muss die der Öffnung zugewandte Seite des Rundschnitts als unwirksam betrachtet werden.<br /> | Liegt der Rand der Lasteinleitungsfläche im Abstand < 6d von einer Öffnung entfernt, so muss die der Öffnung zugewandte Seite des Rundschnitts als unwirksam betrachtet werden.<br /> | ||
Diese ist somit bei der Berechnung abzuziehen <ref name= "Q9">Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchstanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009</ref>. | Diese ist somit bei der Berechnung abzuziehen <ref name= "Q9">Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchstanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009</ref>. | ||
| − | Der Umfang lässt sich somit wie | + | Der Umfang lässt sich somit wie im Bild dargestellt bilden. |
<br /> | <br /> | ||
<br /> | <br /> | ||
Version vom 9. Dezember 2015, 22:15 Uhr
Lasteinleitungsfläche und kritischer Rundschnitt
Die Bemessung der Lasteinleitungsfläche Aload mit dem kritischen Rundschnitt u1 gilt für folgende Geometrien:
- Rundstützen mit dem Umfang
- Rechteckstützen mit und dem Verhältnis von Länge zu Breite
- andere Formen, die sinnvoll wie oben genannt begrenzt werden können
Dabei wird die benötigte statische Nutzhöhe d wie folgt ermittelt:
Die Lasteinleitungsfläche darf sich nicht in der Nähe von anderen konzentrierten Lasten sowie anderen wirkenden Querkräften befinden, was eine Überschneidung der kritischen Rundschnitte zur Folge hätte[1].
Ist dies dennoch der Fall, so ist im Durchstanznachweis der gesamte Rundschnittumfang mit der kleinsten Umhüllenden unter Berücksichtigung der Umfangsbegrenzung der Lasteinleitungsfläche von 12d in Ansatz zu bringen (Nationaler Anhang (NA)) [2].
Einwirkung und Widerstand werden auf den kritischen Rundschnitt bezogen, dieser wird bei Rund- und Rechteckstützen im Abstand 2d von der Lasteinleitungsfläche gebildet (siehe Bild 4) [3].
Die kritische Fläche Acont stellt die Fläche innerhalb des kritischen Rundschnitts u1 dar (siehe Bilder) .
Bei der Ermittlung des kritischen Rundschnitts sind einspringende Ecken zu überlesen, da der kleinste aller Rundschnitte maßgebend ist [3].
Die Berücksichtigung eines Rundschnitts kleiner als 2d ist dann notwendig, wenn ein großer Gegendruck beispielsweise durch Sohldruck bei Fundamenten, einer Auflagerreaktion oder einer Last innerhalb des kritischen Rundschnitts (2d) vorherrscht.
Trifft dieser Fall zu, so ist der Abstand acrit iterativ zu ermitteln (NA) [2]. Sind die oben genannten Bedingungen in Bezug auf die rechteckige Lasteinleitungsfläche nicht erfüllt, so darf nur ein reduzierter kritischer Rundschnitt in Ansatz gebracht werden [4].
Ausgedehnte Einleitungsflächen
Ist das Seitenverhältnis oder der Umfang der Lasteinleitungsfläche , so müssen gesonderte Nachweise geführt werden,
welche nur auf Teilrundschnitte mit zu beziehen sind (siehe Bild).
Der Querkraftwiderstand ist für alle weiteren, über den Umfang hinaus ragenden Bereiche zu ermitteln.
Die Summe aus der Durchstanztragfähigkeit sowie der Querkrafttragfähigkeit bildet den Gesamtwiderstand [3].
Randnähe
Liegt die Lasteinleitungsfläche nahe eines freien Randes, so ist der minimale kritische Rundschnitt möglicherweise nicht mehr geschlossen und endet in diesem Fall stets orthogonal zu diesem [3].
Im zutreffenden Fall ist der Rundschnitt wie im Bild aufgezeigt anzunehmen.
Dieser Rundschnitt wird jedoch nur maßgebend, wenn der Umfang kleiner ist als der des "Regelrundschnitts" bei geschlossener Schnittführung [5].
Beträgt der Abstand zum freien Rand < d, so ist in der Regel eine besondere Randbewehrung einzulegen [1].
Öffnungen
Liegt der Rand der Lasteinleitungsfläche im Abstand < 6d von einer Öffnung entfernt, so muss die der Öffnung zugewandte Seite des Rundschnitts als unwirksam betrachtet werden.
Diese ist somit bei der Berechnung abzuziehen [6].
Der Umfang lässt sich somit wie im Bild dargestellt bilden.
Quellen
- ↑ 1,0 1,1 K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012
- ↑ 2,0 2,1 Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012
- ↑ 3,0 3,1 3,2 3,3 Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript
- ↑ Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
- ↑ G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010
- ↑ Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchstanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009
Seiteninfo 
|