Auflagerelastizitäten (Bsp.): Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
==== Vorgabewerte ==== | ==== Vorgabewerte ==== | ||
| − | + | ||
| + | Die folgenden benutzten Größen sind:<br /> | ||
<br /> | <br /> | ||
| − | <math>I_\mathrm{y} | + | <math>I_\mathrm{y}~....~\mathrm{Flaechentraegheitsmoment}~~~~~~~~\left([I_\mathrm{y}]=\mathrm{m}^{4}\right) </math><br /> |
| + | <math>E~....~\mathrm{Elastizitaetsmodul}~~~~~~~~\left([E]=\mathrm{N}\mathrm{m}^{-2}\right)</math><br /> | ||
| + | <math>l~....~\mathrm{Laenge}~~~~~~~~\left([l]=\mathrm{m}\right)</math><br /> | ||
| + | |||
| + | |||
| + | Aus Nachlagewerk entnommene Werte seien: | ||
| + | <br /> | ||
| + | <math>I_\mathrm{y}=18260\,\mathrm{cm}^{4}</math> <br /> | ||
<math>E=210000\,\mathrm{N}\mathrm{mm}^{-2}</math><br /> | <math>E=210000\,\mathrm{N}\mathrm{mm}^{-2}</math><br /> | ||
<br /> | <br /> | ||
| − | Vorgabe einer selbst definierten Länge: | + | mit der Vorgabe einer selbst definierten Länge: |
<br /> | <br /> | ||
<math>l=5{,}00\,\mathrm{m}</math><br /> | <math>l=5{,}00\,\mathrm{m}</math><br /> | ||
Version vom 1. März 2015, 15:22 Uhr
Beispiel 1 Federsteifigkeit
Aufgabe
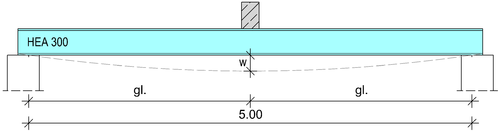
Im folgenden Beispiel wird ein Stahlbetonbalken auf einen Stahlträger (HEA 300) gelagert. Zur Bestimmung der Auflagerelastizität wird die Federsteifigkeit des Trägers ermittelt:
Vorgabewerte
Die folgenden benutzten Größen sind:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{y}~....~\mathrm{Flaechentraegheitsmoment}~~~~~~~~\left([I_\mathrm{y}]=\mathrm{m}^{4}\right) }
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle E~....~\mathrm {Elastizitaetsmodul} ~~~~~~~~\left([E]=\mathrm {N} \mathrm {m} ^{-2}\right)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l~....~\mathrm{Laenge}~~~~~~~~\left([l]=\mathrm{m}\right)}
Aus Nachlagewerk entnommene Werte seien:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{y}=18260\,\mathrm{cm}^{4}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=210000\,\mathrm{N}\mathrm{mm}^{-2}}
mit der Vorgabe einer selbst definierten Länge:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l=5{,}00\,\mathrm{m}}
Berechnung
Durchbiegung unter einer Einzellast in Feldmitte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\cfrac{F\cdot l^{3}}{48\cdot E\cdot I_\mathrm{y}}}
Federsteifigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\cfrac{F}{w} =\cfrac{\cancel{F}\cdot 48\cdot E\cdot I_\mathrm{y}}{\cancel{F}\cdot l^{3}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\cfrac{48\cdot 210000\,\mathrm{N}\mathrm{mm}^{-2}\cdot 18260\,\mathrm{cm}^{4}} {\left(5{,}00\,\mathrm{m}\right)^{3}} =\cfrac{48\cdot 210000\cdot 18260} {5{,}00^{3}}~\cdot ~ \cfrac{\mathrm{N}\mathrm{mm}^{-2}\cdot\mathrm{cm}^{4}} {\mathrm{m}^{3}} =Zahlenwert \cdot \cfrac{10^{-6}\,\mathrm{N}\mathrm{m}^{-2}\cdot 10^{-8}\,\mathrm{m}^{4}} {\mathrm{m}^{3}} =...=\underline{\underline{147249\,\mathrm{kN}\mathrm{m}^{-1}}} }
Quellen
Sonstiges
- Modul-Version: 2014.011
- Autor: R. Wengatz
- Veröffentlicht am: 24.02.2015
- Status: in Bearbeitung