Anschluss von Druck-und Zuggurten: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „==Grundlagen== Plattenbalken sind Träger, bei denen die Biegedruckzone durch Platten neben den Balkenstegen verstärkt wird. Sie müssen schubfest miteina…“) |
|||
| Zeile 31: | Zeile 31: | ||
==Nachweisführung== | ==Nachweisführung== | ||
| + | |||
| + | Die Längskraftdifferenz <math>\Delta F_{cd}~</math> wird in Druckgurten ohne Längskraft N wie folgt ermittelt: | ||
| + | |||
| + | |||
| + | <math>\Delta F_{cd}= \cfrac{\Delta M_{Ed}}{z}\cdot \cfrac{A_{ca}}{A_{cc}}= \cfrac{M_{Ed}}{z}\cdot \cfrac{b_{a}}{b_{eff}}~</math> | ||
| + | |||
| + | Hierin ist: | ||
| + | |||
| + | <math>A_{ca}~</math> - Fläche eine abliegenden Druckflansches | ||
| + | |||
| + | <math>A_{cc}~</math> - Gesamtfläche der Druckzone | ||
| + | |||
| + | <math>b_{a}~</math> - Breite eines abliegenden Flansches | ||
| + | |||
| + | <math>b_{eff}~</math> - Mitwirkende Breite | ||
| + | |||
| + | |||
| + | Falls im Bereich negativer Momente Stäbe der Längsbewehrung ausgelagert wurden, muss hier der Nachweis des Zuggurtes erfolgen. | ||
| + | |||
| + | Die Längskraftdifferenz <math>\Delta F_{sd}~</math> ergibt sich zu: | ||
| + | |||
| + | |||
| + | <math>\Delta F_{sd}= \cfrac{\Delta M_{Ed}}{z}\cdot \cfrac{A_{sa}}{A_{s}}~</math> | ||
| + | |||
| + | <math>A_{sa}~</math> - Fläche der ausgelagerten Bewehrung in '''einem''' Flansch | ||
| + | |||
| + | <math>A_{s}~</math> - Gesamtfläche der Biegezugbewehrung | ||
| + | |||
| + | |||
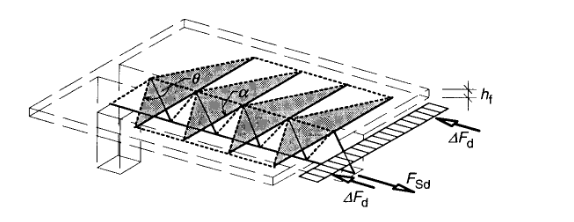
| + | Die Fachwerkanalogie aus der Querkraftbemessung ist für die Nachweisführung wieder anwendbar, nur dass das gedachte Fachwerk nun horizontal in der Platte liegt. Der Nachweis der Druckstrebentragfähigkeit und die Ermittlung der Anschlussbewehrung wird daher nach den Grundsätzen des schon bekannten Verfahrens aus der Querkraftbewehrungsbemessung geführt. Hierbei wird der Hebelarm der inneren Kräfte <math>z~</math> gleich <math>\Delta x~</math> gesetzt und die Querschnittsbreite <math>b_{w}~</math> gleich der Flanschhöhe <math>h_{f}~</math>. | ||
| + | |||
| + | [[Datei:Fachwerk Plattenbalken.PNG]] | ||
| + | |||
| + | So ergibt sich der Nachweis der Druckstrebentragfähigkeit folgendermaßen: | ||
| + | |||
| + | |||
| + | <math>\Delta F_{d} \le V_{Rd,max}~</math> | ||
| + | |||
| + | <math>V_{Rd,max}=\nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x \cdot \cfrac{(cot\theta + cot\alpha)}{(1+cot^2 \theta)}~</math> | ||
| + | |||
| + | |||
| + | Mit dem Druckstrebenwinkel: | ||
| + | |||
| + | <math>cot\theta = \cfrac{(1,2+1,4\cdot \sigma_{cd} / f_{cd})}{(1- V_{Rd,cc}/ \Delta F_{d})}~</math> | ||
| + | |||
| + | mit: | ||
| + | |||
| + | <math>V_{Rd,cc}= [0,24\cdot f_{ck}^{1/3} \cdot (1-1,2\cdot (\cfrac{\sigma_{cd}}{f_{cd}}))]\cdot h_{f}\cdot \Delta x~</math> | ||
| + | |||
| + | |||
| + | Der Bemessungswiderstand für den Schubkraftnachweis: | ||
| + | |||
| + | |||
| + | <math> \Delta F_{d} \le V_{Rd,s}~</math> | ||
| + | |||
| + | <math>V_{Rd,s}=a_{sf}\cdot f_{yd}\cdot \Delta x\cdot (cot\theta+ cot\alpha)\cdot sin\alpha~</math> | ||
| + | |||
| + | |||
| + | Im Regelfall einer lotrechten Bügelbewehrung vereinfachen sich die Formeln: | ||
| + | |||
| + | <math>V_{Rd,max}= \cfrac{\nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x}{tan\theta + cot\theta}~</math> | ||
| + | |||
| + | |||
| + | <math>cot\theta= \cfrac{1,2}{(1-V_{Rd,cc}/ V_{Ed})}~</math> | ||
| + | |||
| + | |||
| + | <math>V_{Rd,s}=a_{sf}\cdot f_{yd}\cdot \Delta x\cdot cot\theta~</math> | ||
| + | |||
| + | |||
| + | Wenn die Druckstrebenneigungswinkel zur Vereinfachung <math>cot\theta=1,2</math> bei Druckgurten und <math>cot\theta=1,0</math> bei Zuggurten angenommen werden erhält man folgenden einfachen Nachweis: | ||
| + | |||
| + | '''Anschluss eines Druckgurtes''' | ||
| + | |||
| + | <math>V_{Rd,max}=0,492\cdot \nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x </math> | ||
| + | |||
| + | <math>a_{sf}=\cfrac{\Delta F_{cd}}{(f_{yd}\cdot \Delta x \cdot 1,2)}</math> | ||
| + | |||
| + | |||
| + | '''Anschluss eines Zuggurtes''' | ||
| + | |||
| + | <math>V_{Rd,max}=0,500\cdot \nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x </math> | ||
| + | |||
| + | <math>a_{sf}=\cfrac{\Delta F_{cd}}{(f_{yd}\cdot \Delta x )}</math> | ||
| + | |||
| + | |||
| + | <div style="border: 2px solid blue; padding: 5px;">'''Hinweis:'''<br /> | ||
| + | In Druckgurten führt es zu einer deutlichen Minderung der erforderlichen Anschlussbewehrung wenn der Druckstrebenneigungswinkel genau ermittelt wird und '''nicht''' mit der Vereinfachung <math>cot\theta=1,2</math> | ||
| + | gerechnet wird.</div><br /> | ||
Version vom 28. April 2016, 17:12 Uhr
Grundlagen
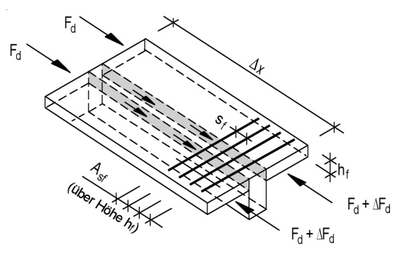
Plattenbalken sind Träger, bei denen die Biegedruckzone durch Platten neben den Balkenstegen verstärkt wird.
Sie müssen schubfest miteinander verbunden sein, um Anteile der Biegedruckkraft Fcd in die Platte übertragen zu können.
Dadurch wird der Steganschnitt durch Schubspannungen belastet und es muss nachgewiesen werden,
dass der gegebene Querschnitt diese übertragen kann. In einem Zuggurt, also in einem Bereich negativer Momente, entstehen nur Beanspruchungen,
wenn ein Teil der Biegezugbewehrung in die Platte ausgelagert wird.
Die übertragenen Schubkräfte breiten sich gleichmäßig bis auf die effektive Plattenbreite in die Flansche aus und erzeugen so Zugkräfte, die rechtwinklig zur Bauteilachse verlaufen.
Es muss daher gegebenenfalls eine Anschlussbewehrung zur Aufnahme dieser Schubkräfte angeordnet werden.
Sie wird quer in den Flansch eingelegt und in der Regel gleichmäßig auf die obere und untere Seite des Flansches verteilt.
Die Bemessungsquerkraft Δ Fcd wird über eine Länge Δ x ermittelt.
Bei gleichmäßig belasteten Trägern sollte Δ x nicht länger als der halbe Abstand zwischen Momentenmaximum und Momentennullpunkt angenommen werden.
In diesem Bereich wird davon ausgegangen, dass die Querkraft annähernd konstant verläuft und das Biegemoment linear veränderlich ist.
Im Fall von auftretenden Einzellasten sollte die Strecke Δ x daher nicht über die Querkraftsprünge hinausgehen.
Nachweisführung
Die Längskraftdifferenz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{cd}~} wird in Druckgurten ohne Längskraft N wie folgt ermittelt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{cd}= \cfrac{\Delta M_{Ed}}{z}\cdot \cfrac{A_{ca}}{A_{cc}}= \cfrac{M_{Ed}}{z}\cdot \cfrac{b_{a}}{b_{eff}}~}
Hierin ist:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{ca}~} - Fläche eine abliegenden Druckflansches
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{cc}~} - Gesamtfläche der Druckzone
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{a}~} - Breite eines abliegenden Flansches
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{eff}~} - Mitwirkende Breite
Falls im Bereich negativer Momente Stäbe der Längsbewehrung ausgelagert wurden, muss hier der Nachweis des Zuggurtes erfolgen.
Die Längskraftdifferenz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{sd}~} ergibt sich zu:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{sd}= \cfrac{\Delta M_{Ed}}{z}\cdot \cfrac{A_{sa}}{A_{s}}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{sa}~} - Fläche der ausgelagerten Bewehrung in einem Flansch
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s}~} - Gesamtfläche der Biegezugbewehrung
Die Fachwerkanalogie aus der Querkraftbemessung ist für die Nachweisführung wieder anwendbar, nur dass das gedachte Fachwerk nun horizontal in der Platte liegt. Der Nachweis der Druckstrebentragfähigkeit und die Ermittlung der Anschlussbewehrung wird daher nach den Grundsätzen des schon bekannten Verfahrens aus der Querkraftbewehrungsbemessung geführt. Hierbei wird der Hebelarm der inneren Kräfte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z~}
gleich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta x~}
gesetzt und die Querschnittsbreite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_{w}~}
gleich der Flanschhöhe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_{f}~}
.
So ergibt sich der Nachweis der Druckstrebentragfähigkeit folgendermaßen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{d} \le V_{Rd,max}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,max}=\nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x \cdot \cfrac{(cot\theta + cot\alpha)}{(1+cot^2 \theta)}~}
Mit dem Druckstrebenwinkel:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot\theta = \cfrac{(1,2+1,4\cdot \sigma_{cd} / f_{cd})}{(1- V_{Rd,cc}/ \Delta F_{d})}~}
mit:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,cc}= [0,24\cdot f_{ck}^{1/3} \cdot (1-1,2\cdot (\cfrac{\sigma_{cd}}{f_{cd}}))]\cdot h_{f}\cdot \Delta x~}
Der Bemessungswiderstand für den Schubkraftnachweis:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta F_{d} \le V_{Rd,s}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,s}=a_{sf}\cdot f_{yd}\cdot \Delta x\cdot (cot\theta+ cot\alpha)\cdot sin\alpha~}
Im Regelfall einer lotrechten Bügelbewehrung vereinfachen sich die Formeln:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,max}= \cfrac{\nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x}{tan\theta + cot\theta}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot\theta= \cfrac{1,2}{(1-V_{Rd,cc}/ V_{Ed})}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,s}=a_{sf}\cdot f_{yd}\cdot \Delta x\cdot cot\theta~}
Wenn die Druckstrebenneigungswinkel zur Vereinfachung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot\theta=1,2}
bei Druckgurten und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot\theta=1,0}
bei Zuggurten angenommen werden erhält man folgenden einfachen Nachweis:
Anschluss eines Druckgurtes
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,max}=0,492\cdot \nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{sf}=\cfrac{\Delta F_{cd}}{(f_{yd}\cdot \Delta x \cdot 1,2)}}
Anschluss eines Zuggurtes
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,max}=0,500\cdot \nu_{1}\cdot f_{cd}\cdot h_{f}\cdot \Delta x }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{sf}=\cfrac{\Delta F_{cd}}{(f_{yd}\cdot \Delta x )}}
In Druckgurten führt es zu einer deutlichen Minderung der erforderlichen Anschlussbewehrung wenn der Druckstrebenneigungswinkel genau ermittelt wird und nicht mit der Vereinfachung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle cot\theta=1,2}
gerechnet wird.