Nachweisführung und Bewehrungsermittlung: Unterschied zwischen den Versionen
| Zeile 82: | Zeile 82: | ||
wobei: | wobei: | ||
| − | <math>C_{Rdc}= \cfrac{0,15}{\gamma_{C}}~</math> | + | <math>C_{Rdc}= \cfrac{0,15}{\gamma_{C}}~</math> - empirisch ermittelter Faktor zur Berücksichtigung eines Bezugszeitraumes von 50 Jahren |
| − | <math>k= 1+ (200/d)^{0,5} \le 2~</math> | + | <math>k= 1+ (200/d)^{0,5} \le 2~</math> - Beiwert zur Berücksichtigung der Bauteilhöhe |
| − | <math>\rho_{l}= \cfrac{A_{sl}}{(b_{w}\cdot d)} \le 0,02~</math> - Längsbewehrungsgrad | + | <math>\rho_{l}= \cfrac{A_{sl}}{(b_{w}\cdot d)} \le 0,02~</math> - Längsbewehrungsgrad; wird auf 2% begrenzt um eine Überbewehrung zu verhindern |
| − | <math>\sigma_{cp}[N/mm^2]= \cfrac{N_{Ed}}{A_{c}}< 0,2\cdot f_{cd}~</math> | + | <math>\sigma_{cp}[N/mm^2]= \cfrac{N_{Ed}}{A_{c}}< 0,2\cdot f_{cd}~</math> - berücksichtigt den Einfluss der Längsspannungen |
<math>b_{w}[mm]</math> - kleinste Querschnittsbreite in der Zugzone | <math>b_{w}[mm]</math> - kleinste Querschnittsbreite in der Zugzone | ||
| + | |||
| + | |||
| + | Bei <math>V_\mathrm{Ed} \le V_\mathrm{Rd,c}~</math>, ist rechnerisch keine Querkraftbewehrung erforderlich. | ||
| + | |||
| + | |||
| + | Es muss aber auch in diesem Fall eine Mindestquerkrafttragfähigkeit eingehalten werden: | ||
| + | |||
| + | <math>V_{Rd,c}\ge (\nu_{min} + 0,12\cdot \sigma_{cp})\cdot b_{w}\cdot d~</math> | ||
| + | |||
| + | mit: | ||
| + | |||
| + | <math>\nu_{min}=(0,0525/\gamma_{C})\cdot k^{3/2}\cdot f_{ck}^{1/2}~</math> für <math>d~</math> ≤ 600mm und | ||
| + | |||
| + | <math>\nu_{min}=(0,0375/\gamma_{C})\cdot k^{3/2}\cdot f_{ck}^{1/2}~</math> für <math>d~</math> > 800mm | ||
| + | |||
| + | |||
| + | Der Nachweis der Betondruckstrebe wird bei Bauteilen ohne Querkraft folgendermaßen geführt: | ||
| + | |||
| + | <math>V_{Ed}\le V_{Rd,max}~</math> | ||
| + | |||
| + | <math>V_{Rd,max}= 0,5\cdot \nu\cdot f_{cd}\cdot b_{w}\cdot d~</math> | ||
| + | |||
| + | mit <math>\nu=~</math> 0,675 | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | 2. <math>V | ||
==Quellen== | ==Quellen== | ||
Version vom 28. April 2016, 10:24 Uhr
Grundlagen
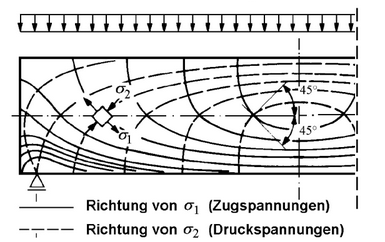
Bei Trägern, die durch Biegemomente und Querkräfte belastet werden, ist folgendes Rissbild zu beobachten.[1]
Es ist zu erkennen, dass die Risse in Bereichen geringer Querkraft fast Vertikal verlaufen, sich aber mit zunehmender Querkraft immer weiter neigen.
Aus diesem Rissbild lässt sich auf den inneren Verlauf der Spannungstrajektorien des Bauteils durch die Krafteinwirkung schliessen.[2]
Dies ist der Verlauf der Hauptspannungen im ungerissenen Zustand (Zustand 1) eines Balkens.
Sobald der Balken durch Rissbildung in den Zustand 2 übergeht verlagern sich die Hauptspannungen, und es wird komplizierter einen genauen Spannungsverlauf zu ermitteln.
Aus diesem Grunde wurden für die Bemessung im Stahlbetonbau einfachere theoretische Modelle entwickelt, die eine möglichst wirklichkeitsnahe Berechnung ermöglichen.
Bei der Querkraftbemessung von Bauteilen wird generell zwischen zwei Fällen unterschieden:
1. Bauteile ohne Querkraftbewehrung:
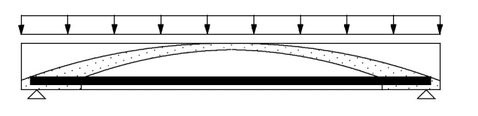
Die Tragwirkung von Bauteilen ohne Querkraftbewehrung wird durch das sogenannte Bogen-Zugband-Modell beschrieben.[2]
Einwirkende Kräfte werden über den entstehenden Druckbogen zu den Auflagern geführt. Sobald das Bauteil in den Zustand 2 übergeht,
kommen weitere Traganteile durch die Kornverzahnung in den gezackten Rissen und durch die Dübelwirkung der Längsbewehrung bei Rissbildung hinzu.[2]
Da die Längsbewehrung hier eine wichtige Rolle bei der Tragwirkung spielt, ist es besonders wichtig sie gut in den Auflagern zu verankern.
2. Bauteile mit Querkraftbewehrung:
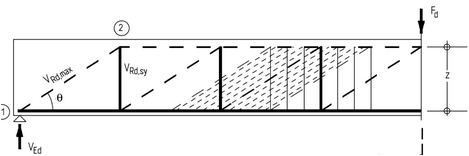
Das Tragverhalten von Bauteilen mit Querkraftbewehrung wird durch das sogenannte Fachwerkmodell idealisiert. [2]
Der Obergurt des Fachwerks wird durch den Beton gebildet und der Untergurt durch die Zugbewehrung.
Die Diagonalen (VRd,max) stellen die Betondruckstreben mit dem dazugehörigen Druckstrebenneigungswinkel phi dar.
Die Vertikalen (VRd,sy) bilden die aufzunehmenden Zugkräfte ab, die durch die Querkraftbewehrung aufzunehmen sind.
Diese können auch geneigt um den Winkel (α) 45°-90° abgebildet werden.
Nachweisführung
Die grundsätzliche Nachweisform für Querkraft im Grenzzustand der Tragfähigkeit lautet:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} \le V_\mathrm{Rd}~}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed}~} - Bemessungswert der einwirkenden Querkraft
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Rd}~} - Bemessungswert der aufnehmbaren Querkraft
Für dem Bemessungswert der aufnehmbaren Querkraft werden drei Widerstände definiert und der einwirkenden Querkraft gegenübergestellt.
In der Regel sind nicht alle 3 erforderlich.
1. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} \le V_\mathrm{Rd,c}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,c}~}
ist der Bemessungswert der aufnehmbaren Querkraft ohne Querkraftbewehrung.
Er wird in der Regel nur bei Platten und untergeordneten Bauteilen verwendet, bei denen nicht zwingend eine Querkraftbewehrung
angeordnet werden muss. Bei Stabförmigen Trägern ist immer eine Mindestquerkraftbewehrung zu ermitteln und der Nachweis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,c}~} entfällt im Normalfall.
Die Größe des Bauteilwiderstandes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,c}~} hängt im Wesentlichen von der Betonzugfestigkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_{ct}~} ab.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,c}= [C_{Rdc}\cdot k\cdot (100\cdot \rho_{l}\cdot f_{ck})^{1/3} + 0,12\cdot \sigma_{cp}]\cdot b_{w}\cdot d~}
wobei:
- empirisch ermittelter Faktor zur Berücksichtigung eines Bezugszeitraumes von 50 Jahren
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k= 1+ (200/d)^{0,5} \le 2~}
- Beiwert zur Berücksichtigung der Bauteilhöhe
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho_{l}= \cfrac{A_{sl}}{(b_{w}\cdot d)} \le 0,02~}
- Längsbewehrungsgrad; wird auf 2% begrenzt um eine Überbewehrung zu verhindern
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{cp}[N/mm^2]= \cfrac{N_{Ed}}{A_{c}}< 0,2\cdot f_{cd}~}
- berücksichtigt den Einfluss der Längsspannungen
- kleinste Querschnittsbreite in der Zugzone
Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed} \le V_\mathrm{Rd,c}~}
, ist rechnerisch keine Querkraftbewehrung erforderlich.
Es muss aber auch in diesem Fall eine Mindestquerkrafttragfähigkeit eingehalten werden:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,c}\ge (\nu_{min} + 0,12\cdot \sigma_{cp})\cdot b_{w}\cdot d~}
mit:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{min}=(0,0525/\gamma_{C})\cdot k^{3/2}\cdot f_{ck}^{1/2}~} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d~} ≤ 600mm und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{min}=(0,0375/\gamma_{C})\cdot k^{3/2}\cdot f_{ck}^{1/2}~} für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d~} > 800mm
Der Nachweis der Betondruckstrebe wird bei Bauteilen ohne Querkraft folgendermaßen geführt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed}\le V_{Rd,max}~}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Rd,max}= 0,5\cdot \nu\cdot f_{cd}\cdot b_{w}\cdot d~}
mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu=~} 0,675
2. <math>V
Quellen
- ↑ Wommelsdorf,O., Stahlbetonbau Bemessung und Konstruktion, 9. Auflage, 0er-Erkenschwick: Werner Verlag, 2008
- ↑ 2,0 2,1 2,2 2,3 Goris,A., Stahlbetonbau-Praxis nach Eurocode 2, Band 1, 5.Auflage, Berlin: Beuth, 2014 Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Name der Quelle1“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert.


![{\displaystyle b_{w}[mm]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/677191b86ae64541ade93b0d40555e27471281e3)