Stahlbetonstütze - Numerisches Verfahren (Bsp.)

Handrechnung

Einwirkungen

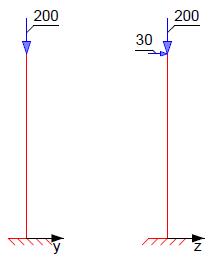
Betongüte: C25/30
Querschnittsabmessungen: b/h = 30/30cm
statische Nutzhöhe: d = 25cm
Bewehrung bereits nach Theorie I. Ordnung vorbemessen und etwas erhöht:
je 6ø14 auf den momentenbeanspruchten gegenüberliegenden Seiten, ${{A}_{s,vorh}}=18,47cm{}^{\text{2}}$

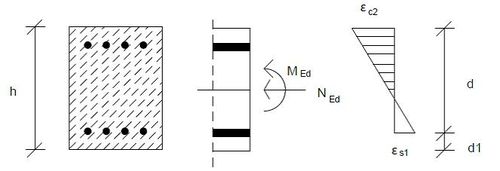
Planmäßige und ungewollte Ausmitte

${\begin{array}{l}{{e}_{0}}={\frac {{M}_{Ed}}{{N}_{Ed}}}={\frac {90}{200}}=0,45m\\{{e}_{i}}={{\Theta }_{i}}\cdot {\frac {{l}_{0}}{2}}={\frac {1}{200\cdot {{\alpha }_{h}}}}\cdot {\frac {{l}_{0}}{2}}={\frac {1}{200\cdot 1}}\cdot {\frac {{l}_{0}}{2}}={\frac {1}{200\cdot 1}}\cdot {\frac {6}{2}}=0,015m\end{array}}$

Vorgehensweise zur Bestimmung der Kopfverschiebung durch numerische Integration, entlehnt aus einem Berechnungsbeispiel von . Hierbei wird die Normalkraft der Stütze vereinfachenderweise vernachlässigt. Aufgrund eines vergleichsweise geringen Drucks von 200kN kommt es zu keiner wesentlich Abweichung im Vergleich zum modulberechneten Ergebnis. Die Druckkraft wirkt sich günstig auf die Krümmung aus, bildet mit der Ausmitte als Hebelarm nach wie vor ein Moment:

Mittlere Betondruckfestigkeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{cd}}=085\cdot {{\alpha }_{cc}}\cdot {{f}_{ck}}=0,85\cdot 0,85\cdot 25=18,06N/mm{}^\text{2}}

Mittlere Stahlzugfestigkeit und –streckgrenze

${\begin{array}{l}{{f}_{yR}}=1,1\cdot {{f}_{yk}}=1,1\cdot 500=550N/mm{}^{\text{2}}\\{{f}_{tR}}=1,08\cdot {{f}_{yR}}=1,08\cdot 550=594N/mm{}^{\text{2}}\end{array}}$

Rissbildungsmoment unter Ansetzung der mittleren Betonzugfestigkeit

${{M}_{cr}}={{f}_{ctm}}\cdot W=0,26\cdot {\frac {30\cdot {{30}^{2}}}{6}}=1170kNcm$

Dehnungen im ungerissenen Zustand

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{c,cr1}}=\frac{{{f}_{ctm}}}{{{E}_{cm}}}=\frac{-0,26}{3100}\cdot 1000=0,0839{}^{o}\!\!\diagup\!\!{}_{oo}\;}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{s,cr1}}=\frac{{{z}_{s1}}}{h/2}\cdot \frac{{{f}_{ctm}}}{{{E}_{cm}}}=\left( \frac{10}{15}\cdot \frac{0,26}{3100} \right)\cdot 1000=0,0559{}^{o}\!\!\diagup\!\!{}_{oo}\;}

Resultierende Krümmung im Zustand I

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\kappa }_{I,II}}=\frac{\left| {{\varepsilon }_{c,cr1}} \right|+\left| {{\varepsilon }_{s,cr1}} \right|}{d}=\frac{0,0839+0,0559}{0,25}\cdot {{10}^{-3}}=0,559\cdot {{10}^{-3}}{{m}^{-1}}}

Verhältnis der E-Moduln

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{e}}=\frac{{{E}_{s}}}{{{E}_{cm}}}=\frac{200000}{31000}=6,4516}

Längsbewehrungsgrad (nur Zugbewehrung)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\rho }_{l}}=\frac{{{A}_{s}}}{b\cdot d}=\frac{18,47\cdot 0,5}{30\cdot 25}=0,0123}

Anteil der Betondruckzone

${\begin{array}{l}\xi =-{{\alpha }_{e}}\cdot {{\rho }_{l}}+{\sqrt {\left({{\alpha }_{e}}\cdot {{\rho }_{l}}\right){}^{\text{2}}+2\cdot {{\alpha }_{e}}\cdot {{\rho }_{l}}}}\\\ \ \ =-6,4516\cdot 0,0123+{\sqrt {\left(6,4516\cdot 0,0123\right){}^{\text{2}}+2\cdot 6,4516\cdot 0,0123}}=0,3269\end{array}}$

Betondruckspannung unter dem Rissbildungsmoment

$-{{\sigma }_{c2}}={\frac {{M}_{cr}}{{\frac {\xi }{2}}\cdot \left(1-{\frac {\xi }{3}}\right)\cdot b\cdot d{}^{\text{2}}}}={\frac {1170}{{\frac {0,3269}{2}}\cdot \left(1-{\frac {0,3269}{3}}\right)\cdot 30\cdot 25{}^{\text{2}}}}=0,4285kN/cm{}^{\text{2}}$

Betonstauchung im Zustand II

${{\varepsilon }_{c,cr2}}={\frac {{\sigma }_{c2}}{{E}_{cm}}}={\frac {-4,285}{31000}}\cdot 1000=-0,1382{}^{o}\!\!\diagup \!\!{}_{oo}\;$

Stahlspannung unter dem Rissbildungsmoment

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\sigma }_{s}}=\frac{1-\xi }{\xi }\cdot \left( -{{\sigma }_{c2}} \right)\cdot {{\alpha }_{e}}=\frac{1-0,3269}{0,3269}\cdot 0,4285\cdot 6,4516=5,6922kN/cm{}^\text{2}}

Stahldehnung im Zustand II

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{s,cr2}}=\frac{{{\sigma }_{s}}}{{{E}_{s}}}=\frac{56,92}{200000}\cdot 1000=0,2846{}^{o}\!\!\diagup\!\!{}_{oo}\;}

mechanischer Bewehrungsgrad (nur Zugbewehrung)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{II}}=\frac{{{A}_{s}}}{b\cdot d}\cdot \frac{{{f}_{yR}}}{{{f}_{cd}}}=\frac{18,47\cdot 0,5}{30\cdot 25}\cdot \frac{550}{18,06}=0,375}

Stahldehnung bei Erreichen der Streckgrenze

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{s}}=\frac{{{f}_{yR}}}{{{E}_{s}}}=\frac{550}{200000}\cdot 1000=2,75{}^{o}\!\!\diagup\!\!{}_{oo}\;}

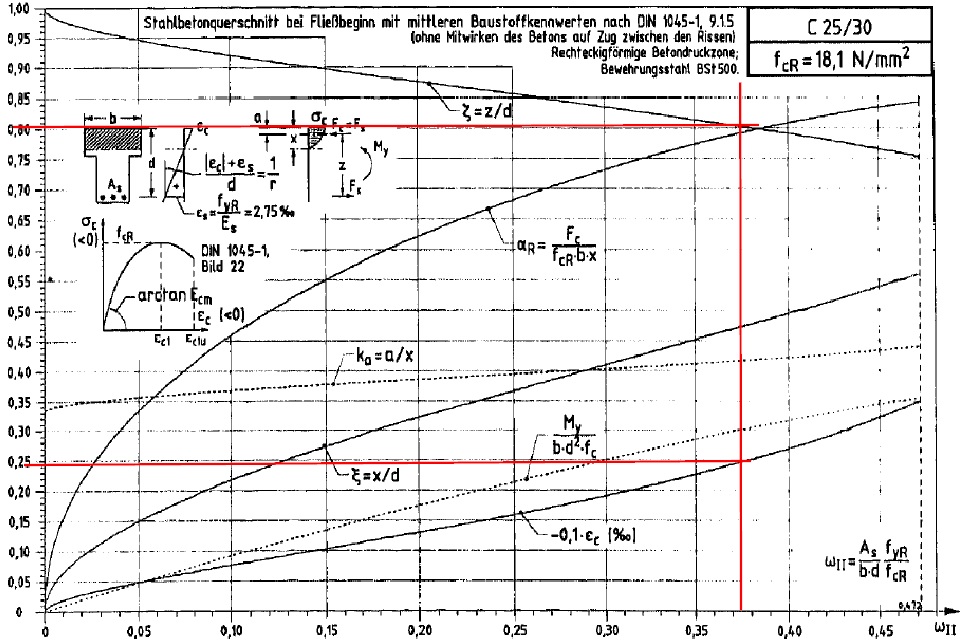
Verwendung der Tafeln nach Schmitz zur Ermittlung der Betonstauchung bei Erreichen der Streckgrenze und des zugehörigen inneren Hebelarms

${\begin{array}{l}{{\varepsilon }_{c}}=-2,4{}^{o}\!\!\diagup \!\!{}_{oo}\;\\\varsigma =0,81\\z=\varsigma \cdot d=0,81\cdot 25=20,25cm\end{array}}$

Fließmoment

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{y}}={{F}_{sd}}\cdot z={{A}_{s}}\cdot {{f}_{yR}}\cdot z=18,47\cdot 0,5\cdot 55\cdot 20,25=102,85kNm}

Stahldehnung reduziert um den Anteil der Zugversteifung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{smy}}={{\varepsilon }_{sy}}-{{\beta }_{t}}\cdot \left( {{\varepsilon }_{sr2}}-{{\varepsilon }_{sr1}} \right)=2,75-0,4\cdot \left( 0,2846-0,0559 \right)=2,66{}^{o}\!\!\diagup\!\!{}_{oo}\;}

zugehörige Mittlere Krümmung

${{\kappa }_{y}}={\frac {{{\varepsilon }_{smy}}+\left|{{\varepsilon }_{c}}\right|}{d}}={\frac {2,66+2,4}{0,25}}\cdot {{10}^{-3}}=20,23\cdot {{10}^{-3}}{{m}^{-1}}$

Wertepaare:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{M}_{I,II}}=11,7kNm\\{{\kappa }_{I,II}}=0,4659\cdot {{10}^{-3}}{{m}^{-1}}\\{{M}_{y}}=102,85kNm\\{{\kappa }_{y}}=20,23\cdot {{10}^{-3}}{{m}^{-1}}\end{array}}

Momenten-Krümmungs-Diagramm

Eine höhere Druckkraft würde hier bei steigendem Moment für gleiche Krümmung (also hier eine höhere Position des Punktes des ersten Wertepaares) sorgen.

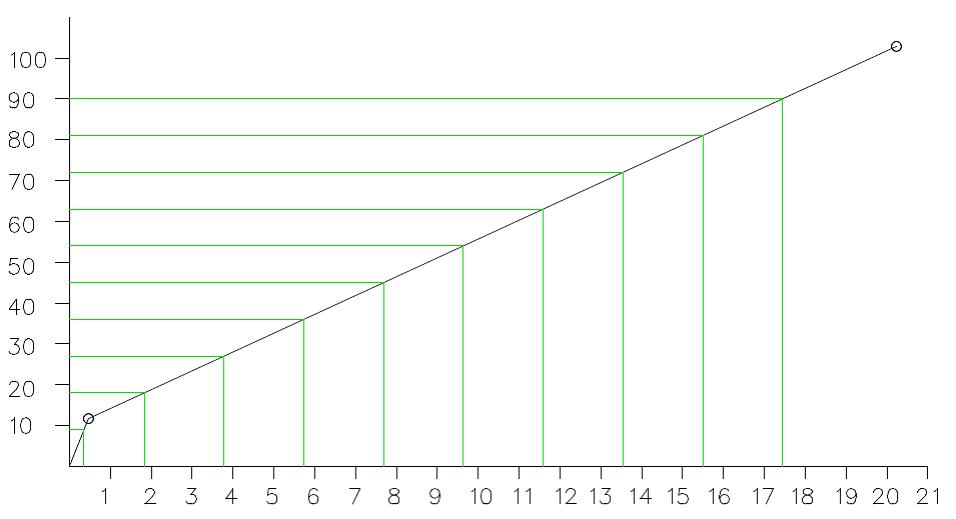
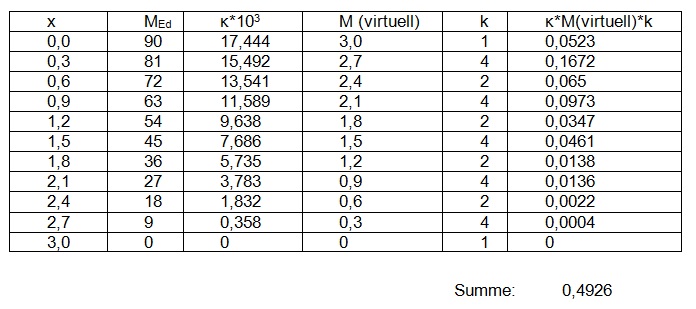
Numerische Integration

Teilung in 10 gleich große Abschnitte Δx = 0,3m
Beschreibung der Simpson-Formel:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}w\left( 3m \right)=\frac{\Delta x}{3}\cdot ({{y}_{0}}+4{{y}_{1}}+2{{y}_{2}}+4{{y}_{3}}+2{{y}_{4}}+4{{y}_{5}}+2{{y}_{6}}+4{{y}_{7}}+2{{y}_{8}}+4{{y}_{9}}+{{y}_{10}})\\\\{{y}_{i}}={{\kappa }_{i}}\cdot {{\overline{M}}_{i}}\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w\left( 3m \right)=\frac{0,3}{3}\cdot 0,4926=0,04926m\quad =\quad {{e}_{2}}}

Gesamtausmitte

${{e}_{tot}}={{e}_{1}}+{{e}_{i}}+{{e}_{2}}=0,45+0,015+0,04926=0,51m~$

resultierendes Moment nach Theorie II. Ordnung

${{M}_{Ed,2}}={{N}_{Ed}}\cdot {{e}_{tot}}=200\cdot 0,51=102kNm$

Bemessung erfolgt nun wie Vorbemessung nach Theorie I. Ordnung mithilfe des Interaktionsdiagramms. Bei Übereinstimmung mit vorgewählter Bewehrung ist der Nachweis beendet, andernfalls erfolgt der nächste Iterationsschritt.

mb-Berechnung

Quellen

Seiteninfo Status: Seite fertig, ungeprüft