Stahlbetonstütze - Verfahren mit Nennkrümmung (Bsp.)

Handrechnung

Einwirkungen

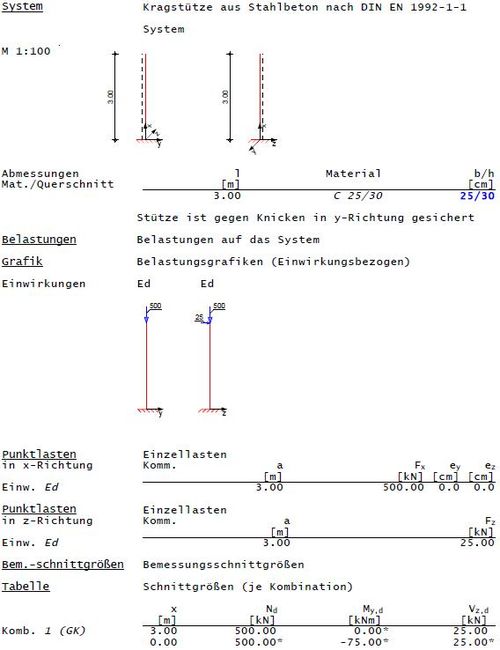
Querschnittsabmessungen, Betongüte und Endkriechzahl

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}b/h=25/30cm\quad \quad {{d}_{1}}=3,5cm\\l=3m\quad \quad \quad \quad \quad \quad C25/30\\\phi \left( \infty ,{{t}_{0}} \right)=2,0\end{array}}

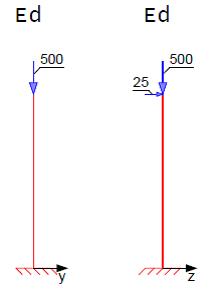
In x-y-Ebene schließen Wände an, die Stütze ist in diese Richtung gehalten.

Schnittgrößen nach Theorie I. Ordnung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{N}_{Ed}}=-500kN\\{{M}_{y,Ed}}=25\cdot 3=75kNm\end{array}}

Schlankheitskriterium

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda =\frac{{{l}_{0}}}{{{i}_{y}}}=\frac{\beta \cdot {{l}_{col}}}{\sqrt{\frac{{{I}_{y}}}{A}}}=\frac{2\cdot 300}{\sqrt{\frac{(25\cdot 30{}^\text{3})/12}{25\cdot 30}}}=69,28}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{-500}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,47}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{\lim }}=25~}

Berücksichtigung von Einwirkungen nach Theorie II. Ordnung erforderlich.

Planmäßige Ausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}=\frac{{{M}_{Ed}}}{{{N}_{Ed}}}=\frac{75}{500}=0,15m}

Ungewollte Ausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}0\le {{\alpha }_{h}}=\frac{2}{{{l}^{0,5}}}\le 1\\{{\alpha }_{h}}=\frac{2}{{{3}^{0,5}}}=1,15\\{{\alpha }_{h}}=1\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}={{\Theta }_{i}}\cdot \frac{{{l}_{0}}}{2}=\frac{1}{200\cdot {{\alpha }_{h}}}\cdot \frac{{{l}_{0}}}{2}=\frac{1}{200\cdot 1}\cdot \frac{6}{2}=0,015m}

Ausmitte nach Theorie II. Ordnung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varphi }_{ef}}=\varphi \left( \infty ,{{t}_{0}} \right)\cdot \frac{{{M}_{0,Eqp}}}{{{M}_{0,Ed}}}=2\cdot \frac{75}{75}=2}

(wegen gegebener Bemessungswerte kann das Moment im GZG nicht genauer ermittelt werden)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =0,35+\frac{{{f}_{ck}}}{200}-\frac{\lambda }{150}=0,35+\frac{25}{200}-\frac{69,28}{150}=0,013}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{K}_{\varphi }}=1+\beta \cdot {{\varphi }_{ef}}\ge 1\\{{K}_{\varphi }}=1+0,013\cdot 2=1,03\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}=1~} (wegen vorerst unbekannter Bewehrung mit 1 angenommen)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{yd}}=\frac{{{f}_{yd}}}{{{E}_{s}}}=\frac{500/1,15}{200000}=2,174\cdot {{10}^{-3}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{{{r}_{0}}}=\frac{{{\varepsilon }_{yd}}}{0,45\cdot d}=\frac{2,174\cdot {{10}^{-3}}}{0,45\cdot (0,3-0,035)}=0,0182{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}={{K}_{r}}\cdot {{K}_{\varphi }}\cdot \frac{1}{{{r}_{0}}}=1\cdot 1,03\cdot 0,0182=0,0188{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}=\frac{1}{r}\cdot l_{0}^{2}\cdot {{K}_{1}}\cdot \frac{1}{c}=0,0188\cdot 6{}^\text{2}\cdot 1\cdot \frac{1}{10}=0,0676m}

Gesamtausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}={{e}_{0}}+{{e}_{i}}+{{e}_{2}}=0,15+0,015+0,0676=0,2326m~}

Resultierendes Moment am Stützenfuß

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2,Ed}}={{N}_{Ed}}\cdot {{e}_{tot}}=500\cdot 0,2326=116,3kNm}

Bezogene Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-500}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,47\\{{\mu }_{Ed}}=\frac{{{M}_{2,Ed}}}{b\cdot h{}^\text{2}\cdot {{f}_{cd}}}=\frac{11630}{25\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,36\end{array}}

Bemessung mit Interaktionsdiagramm für symmetrisch bewehrte Querschnitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{d}_{1}}}{h}=\frac{0,035}{0,3}=0,12\approx 0,1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\omega }_{tot}}=0,61\\{{A}_{s,tot}}={{\omega }_{tot}}\cdot \frac{b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}=0,61\cdot \frac{25\cdot 30}{\frac{50}{1,15}/0,85\cdot \frac{2,5}{1,5}}=14,9cm{}^\text{2}\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s1}}={{A}_{s2}}=\frac{14,9}{2}=7,35cm{}^\text{2}} , gewählt: 5ø14 je Seite, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s,vorh}}=7,7cm{}^\text{2}~}

Weitere Berechnung mit genauerem Krümmungsbeiwert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}=-0,47}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{2\cdot 7,7\cdot \frac{50}{1,15}}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=0,63}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{n}_{u}}=1+\omega =1,63~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}=\frac{{{n}_{u}}-n}{{{n}_{u}}-{{n}_{bal}}}=\frac{1,63-0,47}{1,63-0,4}=0,94}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}={{K}_{r}}\cdot {{K}_{\varphi }}\cdot \frac{1}{{{r}_{0}}}=0,94\cdot 1,03\cdot 0,0182=0,0176{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}=\frac{1}{r}\cdot l_{0}^{2}\cdot {{K}_{1}}\cdot \frac{1}{c}=0,0176\cdot 6{}^\text{2}\cdot 1\cdot \frac{1}{10}=0,0634m}

Gesamtausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}={{e}_{0}}+{{e}_{i}}+{{e}_{2}}=0,15+0,015+0,0634=0,2284m~}

Resultierendes Moment am Stützenfuß

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2,Ed}}={{N}_{Ed}}\cdot {{e}_{tot}}=500\cdot 0,2284=114,22kNm}

Bezogene Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=-0,47\\{{\mu }_{Ed}}=\frac{{{M}_{2,Ed}}}{b\cdot h{}^\text{2}\cdot {{f}_{cd}}}=\frac{11422}{25\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,36\end{array}}

Keine wesentliche Veränderung, Bemessung bleibt bei 2x5ø14.
Anmerkung: die Berechnung mit dem Modul ergibt einen erforderlichen Querschnitt von 0,02cm² über den vorhandenen mit 10ø14 an und verlangt daraufhin 2 weitere Stäbe.

mb-Berechnung

Quellen

Seiteninfo Status: Seite fertig, ungeprüft