Stahlbetonstütze - Verfahren mit Nennsteifigkeit (Bsp.): Unterschied zwischen den Versionen
| Zeile 3: | Zeile 3: | ||
== Aufgabenstellung == | == Aufgabenstellung == | ||
| − | + | [[File:Verfahren mit Nennsteifigkeit (Bsp.) 1.png]]<br /> | |
| + | |||
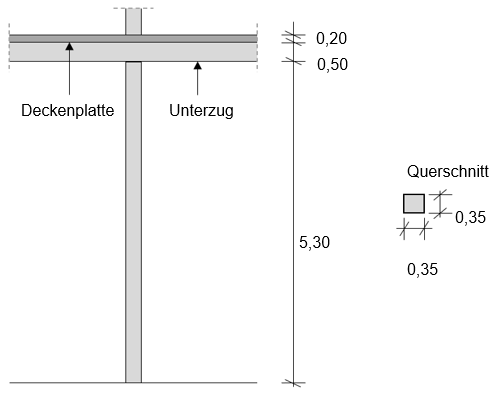
| + | Gegeben ist die dargestellte Hochbau-Innenstütze. Das Gesamt-Bauwerk ist in Richtung der Zeichenebene und senkrecht dazu ausgesteift. Die Stütze wird planmäßig ausschließlich durch Normalkräfte belastet und kann in beide Richtungen ausweichen. | ||
| + | |||
| + | Weiterhin sind folgende Informationen gegeben: | ||
| + | |||
| + | |||
| + | * Beton C25/30 (Innenbauteil – XC 1) | ||
| + | * Stahl B 500 A | ||
| + | * Ständige Last (Stützenkopf) <math>N_{Gk} = - 1.250,0 kN</math> | ||
| + | * Nutzlast (Stützenkopf) <math>N_{Qk} = - 750,0 kN</math> (Nutzlastkategorie C) | ||
| + | * Bewehrungsvorschlag: Øs,L =20 mm, Øs,Bü =20 mm | ||
| + | |||
| + | |||
| + | Es ist die vollständige Bemessung nach dem Verfahren mit Nennsteifigkeit durchzuführen und entsprechende Bewehrung auszuwählen! | ||
== Handrechnung == | == Handrechnung == | ||
Version vom 16. Februar 2022, 19:31 Uhr
Diese Seite ist noch in Bearbeitung.
Aufgabenstellung
Gegeben ist die dargestellte Hochbau-Innenstütze. Das Gesamt-Bauwerk ist in Richtung der Zeichenebene und senkrecht dazu ausgesteift. Die Stütze wird planmäßig ausschließlich durch Normalkräfte belastet und kann in beide Richtungen ausweichen.
Weiterhin sind folgende Informationen gegeben:
- Beton C25/30 (Innenbauteil – XC 1)
- Stahl B 500 A
- Ständige Last (Stützenkopf) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Gk} = - 1.250,0 kN}
- Nutzlast (Stützenkopf) Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Qk} = - 750,0 kN} (Nutzlastkategorie C)
- Bewehrungsvorschlag: Øs,L =20 mm, Øs,Bü =20 mm
Es ist die vollständige Bemessung nach dem Verfahren mit Nennsteifigkeit durchzuführen und entsprechende Bewehrung auszuwählen!
Handrechnung
Schnittgrößen nach Theorie I. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Ed} = {\gamma}_G \cdot N_{Gk} + {\gamma}_Q \cdot N_{Qk} = 1,35 \cdot (-1250 kN) + 1,5 \cdot \cdot (-750 kN) = -2.812,5 kN}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed,y,I} = M_{Ed,z,I} = 0 kNm}
Knicklänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{col} = 6,00 m}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta = 1,0} für das gegebene statische System (Pendelstütze)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_0 = \beta \cdot l_{col} = 1,0 \cdot 6,00 m = 6,00 m}
Schlankheit und Überprüfung der Notwendigkeit des Nachweises nach Theorie II. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda = \frac{l_0}{\sqrt{\frac{I}{A}}} = \frac{600 cm}{35 cm / \sqrt{12}} = 59,38}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle v_{Ed} = \frac{N_{Ed}}{b \cdot h \cdot f_{cd}} = \frac{- 2.812,5 kN}{35 cm \cdot 35 cm \cdot 1,42 kN/cm^2} = - 1,62 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\lambda}_{crit} = \frac{16}{\sqrt{|v_{Ed}}} = \frac{16}{\sqrt{- 1,62}} = 12,57 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\lambda}_{vorh} > max(25; \frac{16}{\sqrt{|v_{Ed}|}}) }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 59,38 > 25 }
Es ist ein Nachweis nach Theorie II. Ordnung nötig.
Nennsteifigkeit
E-Moduln
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_{cd} = \frac{E_{cm}}{{\gamma}_{CE}} = \frac{31.000 N/mm^2}{1,5} = 20.667 N/mm^2 = 2.066,7 kN/cm^2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E_s = 200.000 N/mm^2 }
Flächenträgheitsmoment des Betons
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_c = \frac{b \cdot h^3}{12} = \frac{35 cm \cdot (35 cm)^2}{12} = 125.052 cm^4 }
Planmäßige Lastausmitte und Lastausmitte aus Imperfektionen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e_0 = 0 cm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_h = \frac{2}{\sqrt{l}} = \frac{2}{\sqrt{6,0}} = 0,816 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\theta}_i = \frac{1}{200} \cdot {\alpha}_h = \frac{1}{200} \cdot 0,816 = \frac{1}{245} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e_i = {\theta}_i \cdot \frac{l_0}{2} = \frac{1}{245} \cdot \frac{600 cm}{2} = 1,22 cm }
Vorbemessung
Wirksame Bauteildicke
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_0 = \frac{2 \cdot A_c}{u} = \frac{2 \cdot (35 cm)^2}{4 \cdot 35 cm} = 17,5 cm }
Endkriechzahl
Erstbelastung des Betons: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_0 = 28 } Tage
Bauteil in Innenräumen, trockene Umgebungsbedingungen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\phi}_{\infty, t0} = 2,8} nach Schneider 5.33
Moment mit Imperfektionen in quasi-ständiger und GZT-Kombination
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{1,perm} = (|N_{Gk}| + {\psi}_2 \cdot |N_{Qk}|) \cdot e_i = (1.250 kN + 0,6 \cdot 750 kN) \cdot 0,0122 m = 20,74 kNm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{1,Ed} = ({\gamma}_{Gk} \cdot |N_{Gk}| + {\gamma}_{Qk} \cdot |N_{Qk}|) \cdot e_i = (1,35 \cdot 1.250 kN + 1,5 \cdot 750 kN) \cdot 0,0122 m = 34,31 kNm }
Effektive Kriechzahl
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\phi}_{ef} = {\phi}_{\infty, t0} \cdot \frac{M_{1,perm}}{M_{Ed}} = 2,8 \cdot \frac{20,74 kNm}{34,31 kNm} = 1,69 }
Steifigkeitsbeiwerte nach einfacher Formel
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_s = 0 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_c = \frac{0,3}{(1 + 0,5 \cdot {\phi}_{ef})} = \frac{0,3}{(1 + 0,5 \cdot 1,69)} = 0,163 }
Vorläufige Nennsteifigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle EI = K_c \cdot E_{cd} \cdot I_c + K_s \cdot E_s \cdot I_s = 0,163 \cdot 2.066,7 kN/cm^2 \cdot 125.052 cm^4 + 0 = 42.126.530 kNcm^2 }
Knicklast
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_B = \frac{EI \cdot \pi^2}{l_0^2} = \frac{42.126.530 kNcm^2 \cdot \pi^2}{(600 cm)^2} = 1.154,9 kN }
Beiwert für den Momentenverlauf
Das Moment stammt aus der Lastausmitte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e_i} für Imperfektionen. Hierbei handelt es sich um eine ungewollte Schiefstellung der Stütze, deshalb ist der Momentenverlauf dreieckig, damit gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_0 = 12} .
Platzhalter für Bild Schiefstellung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta = \frac{\pi^2}{c_0} = \frac{\pi^2}{12} = 0,822 }
Vorläufiges Moment nach Theorie II. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed} = M{0Ed} \cdot (1 + \frac{\beta}{N_B/N_{Ed} - 1}) = 3.431 kNcm \cdot (1 + \frac{0,822}{1.154,9 kN / 2.812,5 kN - 1}) = 3.431 kNcm = 3.431 kNcm \ cdot (-0,39) }
Der Beiwert zur Erhöhung des Moments nach Theorie I. Ordnung ist negativ geworden, weil die Knicklast Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_B} kleiner ist als die einwirkende Normalkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_{Ed}} . Damit liefert die Formel kein brauchbares Ergebnis. Die Vorbemessung muss deshalb mit alternativem Ansatz durchgeführt werden.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed} = |N_{Ed}| \cdot \frac{h}{20} = |- 2.812,5 kN| \cdot \frac{35 cm}{20} = 4.922 kNcm = 49,22 kNm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c_{nom} = c_{min} + \delta c_{dev} = 10 mm + 10 mm = 20 mm }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d_1 = c_{nom} + {\O}_{s,Bu} + {\O}_{s,L}/2 = 2,0 + 1,0 + 2,0/2 = 4,0 cm }
Vorbemessung mit Bewehrungswahl
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{d_1}{h} = \frac{4 cm}{35 cm} = 0,11 \approx 0,10 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\mu}_{Ed} = \frac{M_{Ed}}{b \cdot h^2 \cdot f_{cd}} = \frac{4.922 kNcm}{35 cm \cdot (35 cm)^2 \cdot 1,42 kN/cm^2} = 0,081 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\nu}_{Ed} = \frac{N_{Ed}}{b \cdot h \cdot f_{cd}} = \frac{- 2.812,5 kN}{35 cm \cdot 35 cm \cdot 1,42 kN/cm^2} = - 1,62 }
→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\omega}_{tot} = 0,865 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,tot} = {\omega}_{tot} \cdot b \cdot h \cdot \frac{f_{cd}}{f{yd}} = 0,865 \cdot 35 cm \cdot 35 cm \cdot \frac{1,42 kN/cm^2}{43,5 kN/cm^2} = 34,59 cm^2 }
Gewählt: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 12 \O 20 mm} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 37,68 cm^2}
Genauere Steifigkeitsbeiwerte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_s = 1 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_1 = \sqrt{f_{ck}/20} = \sqrt{25/20} = 1,12 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k_2 = {\nu}_{Ed} \cdot \frac{\lambda}{170} = 1,62 \cdot \frac{59,38}{170} = 0,57 \leq \textbf{0,20} }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle K_c = \frac{k_1 \cdot k_2}{(1 + {\phi}_{ef}} = \frac{1,12 \cdot 0,20}{(1 + 1,69} = 0,083 }
Flächenträgheitsmoment der Bewehrung
Platzhalter für Skizze
Insgesamt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 12 \O 20 mm} mit je Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_s = 3,14 cm^2} . Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. 8 Stäbe mit Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_1 = 13,5 cm} und 4 Stäbe mit Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_2 = 9,5 cm} .
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_s = 12 \cdot \frac{\pi \cdot d^4}{64} + 8 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2 = 12 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 8 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2 = 9 cm^4 + 4.578 cm^4 + 1.134 cm^4 = 5.721 cm^4 }
Bemessung
Nennsteifigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle EI = K_c \cdot E_{cd} \cdot I_c + K_s \cdot E_s \cdot I_s = 0,083 \cdot 2.066,7 kN/cm^2 \cdot 125.052 cm^4 + 1,0 \cdot 20.000 kN/cm^2 \cdot 5.721 cm^4 = 135.870.932 kNcm^2 }
Knicklast
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_B = \frac{EI \cdot \pi^2}{l_0^2} = \frac{135.870.932 kNcm^2 \cdot \pi^2}{(600 cm)^2} = 3.724,98 kN }
Bemessungsmoment nach Theorie II. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed} = M{0Ed} \cdot (1 + \frac{\beta}{N_B/N_{Ed} - 1}) = 3.431 kNcm \cdot (1 + \frac{0,822}{3.724,98 kN / 2.812,5 kN - 1}) = 3.431 kNcm = 12.124 kNcm }
Bewehrungswahl
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\mu}_{Ed} = \frac{M_{Ed}}{b \cdot h^2 \cdot f_{cd}} = \frac{12.124 kNcm}{35 cm \cdot (35 cm)^2 \cdot 1,42 kN/cm^2} = 0,199 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\nu}_{Ed} = \frac{N_{Ed}}{b \cdot h \cdot f_{cd}} = \frac{- 2.812,5 kN}{35 cm \cdot 35 cm \cdot 1,42 kN/cm^2} = - 1,62 }
→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\omega}_{tot} = 1,22 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,tot} = {\omega}_{tot} \cdot b \cdot h \cdot \frac{f_{cd}}{f{yd}} = 1,22 \cdot 35 cm \cdot 35 cm \cdot \frac{1,42 kN/cm^2}{43,5 kN/cm^2} = 48,79 cm^2 }
Damit ist . Der Nachweis ist nicht erfüllt, die Bewehrung muss entweder von der Anzahl oder dem Durchmesser her erhöht werden.
Iteration: Mehr Bewehrungsstäbe
Erhöhung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 12 \O 20mm} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16 \O 20 mm} . Neues Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 50,24 cm^2} .
Flächenträgheitsmoment der Bewehrung
Platzhalter für Skizze
Insgesamt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 16 \O 20 mm} mit je Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_s = 3,14 cm^2} . Alle Abstände sind bezogen auf den Mittelpunkt des Betonquerschnitts. 10 Stäbe mit Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_1 = 13,5 cm} , 4 Stäbe mit Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_2 = 9,5 cm} und 2 Stäbe mit Abstand s_3 = 0 cm</math>.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_s = 16 \cdot \frac{\pi \cdot d^4}{64} + 10 \cdot A_s \cdot s_1^2 + 4 \cdot A_s \cdot s_2^2 = 16 \cdot \frac{\pi \cdot (2,0 cm)^4}{64} + 10 \cdot 3,14 cm^2 \cdot (13,5 cm)^2 + 4 \cdot 3,14 cm^2 \cdot (9,5 cm)^2 = 13 cm^4 + 5.723 cm^4 + 1.134 cm^4 = 6.870 cm^4 }
Bemessung
Nennsteifigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle EI = K_c \cdot E_{cd} \cdot I_c + K_s \cdot E_s \cdot I_s = 0,083 \cdot 2.066,7 kN/cm^2 \cdot 125.052 cm^4 + 1,0 \cdot 20.000 kN/cm^2 \cdot 6.870 cm^4 = 158.850.932 kNcm^2 }
Knicklast
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_B = \frac{EI \cdot \pi^2}{l_0^2} = \frac{158.850.932 kNcm^2 \cdot \pi^2}{(600 cm)^2} = 4.354,99 kN }
Bemessungsmoment nach Theorie II. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_{Ed} = M{0Ed} \cdot (1 + \frac{\beta}{N_B/N_{Ed} - 1}) = 3.431 kNcm \cdot (1 + \frac{0,822}{4.354,99 kN / 2.812,5 kN - 1}) = 3.431 kNcm = 8.573 kNcm }
Bewehrungswahl
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\mu}_{Ed} = \frac{M_{Ed}}{b \cdot h^2 \cdot f_{cd}} = \frac{8.573 kNcm}{35 cm \cdot (35 cm)^2 \cdot 1,42 kN/cm^2} = 0,141 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\nu}_{Ed} = \frac{N_{Ed}}{b \cdot h \cdot f_{cd}} = \frac{- 2.812,5 kN}{35 cm \cdot 35 cm \cdot 1,42 kN/cm^2} = - 1,62 }
→ Ermittlung des Bewehrungsgrads durch Interaktionsdiagramm für umfangsverteilte Bewehrung (Quelle)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\omega}_{tot} = 1,045 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,tot} = {\omega}_{tot} \cdot b \cdot h \cdot \frac{f_{cd}}{f{yd}} = 1,045 \cdot 35 cm \cdot 35 cm \cdot \frac{1,42 kN/cm^2}{43,5 kN/cm^2} = 41,79 cm^2 }
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{s,vorh} = 50,24 cm^2 > 41,79 cm^2 = A_{s,erf} }
Platzhalter Bewehrungsskizze