Zwangsarten

Unterscheidung in inneren und äußeren Zwang

Arten der Verformungsbehinderung beim Auftreten von äußerem Zwang

Zwänge entstehen immer dann, wenn die Verformungen eines Bauteils behindert werden. In der Fachliteratur werden die Begriffe innerer und äußerer Zwang nur selten verwendet.
In „Wommelsdorff“ werden die Begriffe durch das Auftreten der Zwangsursache und der Zwangsauswirkung voneinander abgegrenzt. Beim inneren Zwang treten die Ursache, z. B. das Abfließen der Hydratationswärme oder das Schwinden, und die Auswirkung also die entstehenden Spannungen am selben Bauteil auf. Beim äußeren Zwang hingegen entstehen die Zwangsursache und die Zwangsauswirkung an unterschiedlichen Bauteilen.
„Zilch & Zehetmaier“ definieren den inneren Zwang über Verformungen, die sich im Bauteilquerschnitt nicht einstellen können und Eigenspannungen erzeugen. Als Beispiel wird auch hier das Abfließen der Hydratationswärme und das Bauteilschwinden benannt. Durch eine Verformungsbehinderung oder eine aufgezwungene Verformung von außen wird das betrachtete Bauteil durch Spannungen infolge des äußeren Zwangs beansprucht. Beispiele hierfür sind ungleichmäßige Setzungen und Schwindvorgänge in benachbarten Bauteilen.
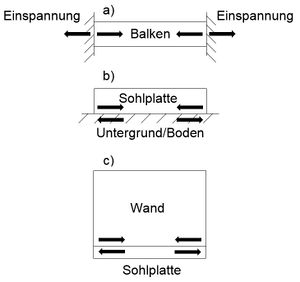
Die Definition der Zwangsarten nach „Röhling“ stimmt mit denen von „Zilch & Zehetmaier“ überein. Beim äußeren Zwang wird jedoch in eine Behinderung am Bauteilende und am Bauteilrand unterschieden. Tritt die Verformungsbehinderung am Bauteilende auf, wie dies z.B. bei Balken oder in Mittelbereichen von Deckenplatten der Fall ist, wird das Bauteil durch zentrische Zwangsspannungen, wenn keine Lasten auf das Bauteil wirken, belastet. Wird das betrachtete Bauteil mittels Arbeitsfuge an ein vorher erstelltes Bauteil angeschlossen, wie dies meist bei dem Betonieren einer Wand auf eine Sohlplatte der Fall ist, entstehen neben den zentrischen auch exzentrische bzw. außermittige Zwangsbeanspruchungen. Durch die flächige Behinderung eines Bauteilrandes, z.B. beim Aufliegen einer Sohlplatte auf dem Untergrund, werden neben den zentrischen und exzentrischen Zwangsspannungen Biegemomente hervorgerufen.
Alle drei oben genannten Fachliteraturquellen stimmen in folgenden Punkten überein. Die statische Bestimmtheit hat keinen Einfluss auf die Entstehung von inneren Zwängen. Voraussetzung für das Auftreten von äußeren Zwängen ist ein statisch unbestimmtes System. Hierbei werden Schnittgrößen im Querschnitt erzeugt, die Auflagerreaktionen benachbarter Bauteile hervorrufen.
In der einschlägigen Norm DIN EN 1992-1-1 werden die Begriffe innerer und äußerer Zwang nicht mehr verwendet. Es ist nur noch die Rede von „Zugspannungen infolge am Bauteil selbst hervorgerufenen Zwangs“ oder von „Zugspannungen infolge außerhalb des Bauteils hervorgerufenen Zwangs“.
Letztlich geht es bei der Unterscheidung zwischen innerem und äußerem Zwang um die Frage, inwieweit nichtlinear verteilte Eigenspannungen ganz oder teilweise Bestandteil der Zwangsbeanspruchungen sind.

Unterscheidung in frühen und späten Zwang

Neben der Unterscheidung abhängig von der Verformungsbehinderung können Zwangsbeanspruchungen auch in frühen oder späten Zwang eingeteilt werden. Diese Differenzierung bezieht sich auf das zeitliche Auftreten der Zwangsbeanspruchungen.
Der frühe Zwang entsteht während der Erhärtung im Betonbauteil, bei mittleren Bauteildicken in den ersten 3 bis 5 Tagen nach dem Betonieren. In diesem Zeitraum können als Zwangsursachen das Abfließen der Hydratationswärme und das chemische und autogene Schwinden benannt werden.
Die Einteilung in den späten Zwang erfolgt vereinfacht nach dem Abfließen der Hydratationswärme, also nach der Erhärtung. Temperaturänderungen im Tages- und Jahresverlauf, Setzungen und das Trocknungsschwinden werden hier eingeordnet.
In der Norm DIN EN 1992-1-1 werden diese beiden Begriffe als Grundlage für den Ansatz der Betonzugfestigkeit verwendet. Da beim frühen Zwang die Festigkeitsentwicklung noch nicht abgeschlossen ist, darf diese verringert angesetzt werden. Beim späten Zwang hingegen sind die Normwerte der Festigkeit erreicht und es muss die mittlere Zugfestigkeit, mindestens jedoch ein Wert von 3,0 N/mm² angesetzt werden. Ausführlicher wird die Thematik der Berechnung im Kapitel Zwang - Mindestbewehrung zur Rissbreitenbegrenzung behandelt.

Spannungsanteile

Spannungsanteile bei einer Temperatureinwirkung

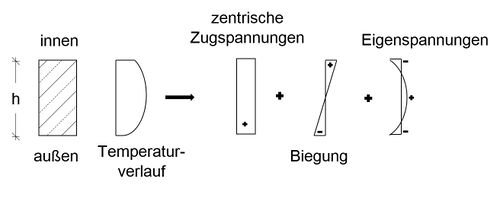
Grundsätzlich kann jede Normalspannungsverteilung als Gesamtwirkung aus folgenden drei Spannungsanteilen betrachtet werden:

• konstante Spannungen
• linear veränderliche Spannungen
• verbleibende nichtlineare Spannungen (Eigenspannung)

Dies gilt natürlich auch für Zwangsspannungen. Bei reinem äußeren Zwang entfällt der Anteil nichtlinearer Eigenspannungen.

konstante Spannungen

Eine konstante Spannungsverteilung über den Querschnitt wird auch als zentrische Zwangsspannung bezeichnet. Zentrische Zwangsspannungen treten sowohl bei innerem als auch bei äußerem Zwang auf und entstehen zum Beispiel durch das Abfließen der Hydratationswärme oder das Bauteilschwinden. Übersteigen die entstehenden Spannungen die Betonzugfestigkeit, entstehen Trennrisse, die durch das Bauteil verlaufen. Die Breite dieser Risse muss durch eine Mindestbewehrung nach DIN EN 1992-1-1 begrenzt werden.

linear veränderliche Spannungen

Bei einer linearen Spannungsverteilung entsteht im Querschnitt ein Biegemoment. Dieses Biegemoment sorgt beim Überschreiten der Betonzugfestigkeit auf der Zugseite für die Entstehung von Biegerissen. Auch diese Risse müssen durch die oben genannte Mindestbewehrung begrenzt werden.
Eine lineare Spannungsverteilung entsteht zum Beispiel, wenn ein Bauteil einer Temperaturdifferenz zwischen Innen- und Außenseite ausgesetzt ist.

verbleibende nichtlineare Spannungen (Eigenspannung)

Verteilung der Temperatur und der Spannungen im Bauteilquerschnitt

Verteilung der Feuchtigkeit und der Spannungen im Bauteilquerschnitt

Die verbleibenden nichtlinearen Spannungen im Bauteilquerschnitt werden auch als Eigenspannungen bezeichnet.
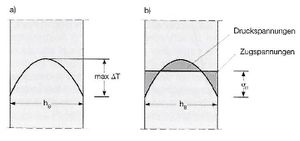
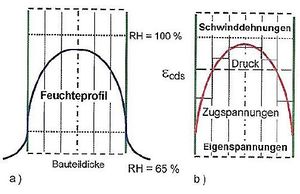
Ausschließlich nichtlinear verteilte Spannungen entstehen nur, wenn sich das Bauteil ansonsten frei verformen kann und ihm von außen keine Verformung aufgezwungen wird. Nichtlinear verteilte Spannungen setzen i. d. R. eine nichtlineare Temperaturverteilung, z. B. durch das Abfließen der Hydratationswärme, oder eine nichtlineare Feuchtigkeitsverteilung, z. B. durch Schwindvorgänge, über den Querschnitt voraus. Wie aus den nebenstehenden Bildern zu erkennen ist, ähneln sich beide Verteilungen, nur zeitlich liegen diese auseinander.
Die nichtlineare Temperaturverteilung infolge der Wärmeentwicklung im jungen Beton entsteht innerhalb der ersten Tage nach dem Betonieren. Aufgrund der höheren Temperatur des Bauteilkernes möchte dieser sich ausdehnen, wird aber vom kühleren Rand an seiner Verformung gehindert. Hieraus resultieren Druckspannungen im Kern und Zugspannungen am Rand, welche bis zum Erreichen des Temperaturmaximums in ihrer Größe ansteigen. Wird das Bauteil innerhalb dieses Zeitraumes ausgeschalt, kühlt sich die Bauteiloberfläche weiter ab und die Zugspannungen am Bauteilrand erhöhen sich. Bei einer Temperaturdifferenz zwischen dem Kern und dem Rand des Bauteils von ΔT ≥ 15 K kann es an der Bauteiloberfläche zu Rissen kommen.
Eine nichtlineare Feuchtigkeitsverteilung entsteht durch das Austrocknen des Querschnittes. Aufgrund der Feuchtigkeitsabgabe an die Umgebungsluft zieht sich der Beton am Bauteilrand zusammen. Diese Volumenverringerung infolge des Schwindens wird durch den feuchteren Bauteilkern behindert. Am Bauteilrand entstehen somit Zug- und im Bauteilkern Druckspannungen.
Sowohl aus der Temperatur- als auch aus der Feuchtigkeitsverteilung lassen sich unter dem Grundsatz des Ebenbleibens der Querschnitte Dehnungsprofile ableiten. Bei Bauteilen größerer Dicke sind diese Dehnungsprofile stärker ausgebildet als bei Bauteilen geringerer Dicke und daher nicht zu vernachlässigen. Eine Einschränkung der auftretenden Dehnungen erfolgt durch die gegenseitige Behinderung der Bauteilfasern oder durch die Behinderung des Schwindens des Betons in der Nähe des Bewehrungsstahls.
Die Größe der nichtlinear verteilten Spannungen ist abhängig von der Größe der Dehnungsdifferenz zwischen Bauteilkern und -rand. Übersteigen die Zugspannungen am Bauteilrand die zu diesem Zeitpunkt wirksame Zugfestigkeit des Betons, entstehen in der Bauteiloberfläche Schalen- bzw. Oberflächenrisse mit geringer Tiefe, welche die Wasserundurchlässigkeit des Bauteils nicht beeinträchtigen. Dies ist z. B. bei einer Temperaturdifferenz zwischen Bauteilkern und Bauteilrand von ΔT ≥ 15 K der Fall. Beim Abkühlen des Bauteils entstehen am Bauteilrand Druckspannungen, welche die Risse verschließen. Eine Schädigung des Betonquerschnittes bleibt jedoch bestehen und kann Ausgangspunkt weiterer Risse sein.

Behinderungsgrad

Verteilung der Temperatur und der Spannungen im Bauteilquerschnitt

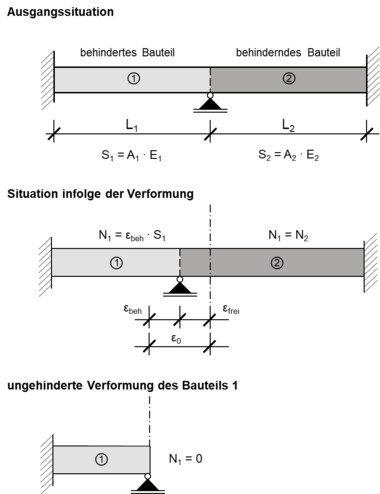
Um abschätzen zu können, wie stark die Verformungen eines Bauteils behindert werden, kann ein Behinderungsgrad ermittelt werden. Dieser Behinderungsgrad kann sowohl für eine reine Dehnbehinderung als auch für eine Krümmungsbehinderung definiert werden.
Der Grad der Dehnungsbehinderung R lässt sich nach aus dem Verhältnis der behinderten Dehnung Δε_beh zur Gesamtdehnung ε₀ ermitteln.

$R=1-{\cfrac {\epsilon _{frei}}{\epsilon _{0}}}={\cfrac {\epsilon _{beh}}{\epsilon _{0}}}$

$\epsilon _{frei}$	freie Dehnung
$\epsilon _{0}$	Gesamtdehnung, die dem Bauteil aufgezwungen wird (Dehnung, die das Bauteil bei ungehinderter Verformung realisieren würde)
$\epsilon _{beh}$	Dehnung, die behindert wird und sich nicht einstellen kann
	$\epsilon _{beh}=\epsilon _{0}-\epsilon _{frei}$

Der Grad der Dehnungsbehinderung kann auch aus dem Verhältnis der Steifigkeiten des behindernden und des behinderten Bauteils ermittelt werden.

$R={\cfrac {S_{2}\cdot L_{1}}{S_{1}\cdot L_{2}+S_{2}\cdot L_{1}}}$

$S_{1}=A_{1}\cdot E_{1}$	Dehnsteifigkeit für das behinderte Bauteil
$S_{2}=A_{2}\cdot E_{2}$	Dehnsteifigkeit für das behindernde Bauteil
$A$	Querschnittsfläche
$E$	Elastizitätsmodul
$L_{1}$	Länge des behinderten Bauteils
$L_{2}$	Länge des behindernden Bauteils

Aufgrund des ansteigenden Elastizitätsmoduls und der damit ansteigenden Steifigkeit beim Erhärten des behinderten Bauteils ist der Behinderungsgrad nicht konstant und nimmt mit zunehmendem Bauteilalter ab. Durch Risse verringert sich die Steifigkeit im Bauteil, sodass sich der Behinderungsgrad erhöht und die Gefahr der weiteren Rissbildung ansteigt.
Je größer der Wert des Behinderungsgrades ist, desto mehr wird die freie Verformungsfähigkeit des behinderten Bauteils eingeschränkt. Bei einem Behinderungsgrad von R = 1,0 ist die freie Verformung vollständig behindert und man spricht vom „vollen Zwang“. Meist ergibt sich der Behinderungsgrad jedoch zu R < 1,0, sodass sich das behinderte Bauteil verformen kann und vom „teilweisen Zwang“ die Rede ist.
Die Krümmungsbehinderung entsteht durch eine über den Querschnitt linear verteilte Dehnung und ist wie nachfolgend definiert.

$K={\cfrac {I_{2}\cdot E_{2}}{I_{1}\cdot E_{1}+I_{2}\cdot E_{2}}}$

$I_{1}$	Trägheitsmoment des behinderten Bauteils
$I_{2}$	Trägheitsmoment des behindernden Bauteils
$E_{1}$	Elastizitätsmodul des behinderten Bauteils
$E_{2}$	Elastizitätsmodul des behindernden Bauteils

In Kombination mit der Dehnungsbehinderung führt die Behinderung der Krümmung zu einer Spannungsverteilung aus zentrischen Zwangsspannungen über die Wandhöhe.
Bei einem biegesteifen Auflager ist die Krümmung vollständig behindert und es treten neben den horizontalen Zwangsschnittgrößen Vertikalkräfte auf, die zu horizontalen Rissen in z.B. der Arbeitsfuge zwischen einer Wand und einer Sohlplatte, führen. Bei einem biegeweichen Auflager hingegen kann sich eine Krümmung einstellen, sodass in der Verbundfuge keine Vertikalkräfte entstehen und die Spannungsverteilung zum Wandkopf hin auf Null fällt.

Verringerung der Zwangsbeanspruchung

Durch eine Verringerung der Bauteiltemperatur können die Dehnungen im Bauteil verringert werden, sodass die entstehenden Zugspannungen eine geringere Größe annehmen. Dies bezieht sowohl die Bauteilerwärmung vor dem Abfließen der Hydratationswärme, beeinflussbar durch die Menge und die Art des Zementes, als auch die Erwärmung infolge Sonneneinstrahlung mit ein. Außerdem kann durch entsprechende Maßnahmen der Zeitraum bis zum Erreichen der Maximaltemperatur im Bauteilquerschnitt verlängert werden, sodass sich am Bauteilrand eine größere Zugfestigkeit entwickeln kann.
Durch eine Dämmung des Bauteils nach dem Betonieren, kann zum Beispiel die Temperaturdifferenz im Bauteilquerschnitt verringert werden, sodass geringere Eigenspannungen entstehen. Es ist jedoch darauf zu achten, dass hierbei die Bauteiltemperatur im Gesamten angehoben wird und dadurch beim Abfließen der Hydratationswärme größere Zugspannungen entstehen.
Zusätzlich dazu sollte das Bauteil möglichst langsam abkühlen und austrocknen, damit die Relaxation langsam entstehende Zugspannungen abbauen kann.
Neben betontechnologischen Maßnahmen können die entstehenden Spannungen auch durch eine konstruktive Verringerung der Verformungsbehinderungen reduziert werden. Bei der Planung von Sohlplatten sollte die Gleitfähigkeit auf dem Untergrund beachtet bzw. sichergestellt werden und in Wänden verringert die Anordnung von Fugen die Zwangsspannungen.

Quellen

Fachliteratur / Normen

Seiteninfo Status: Seite in Bearbeitung