Momentenabminderung an Zwischenauflagern und bei Einzelfundamenten

Idealisierung der Auflager

Um ein Bauwerk berechnen zu können, werden zuerst die tragenden Elemente idealisiert, um ein statisches System zu erhalten. Mit diesem System können dann die Schnittkräfte ermittelt werden. Bei der tatsächlichen Auflagerung handelt es sich jedoch niemals um eine Punktlagerung wie in der angenommenen Idealisierung, sondern um Auflager mit einer bestimmten Breite. Um eine Überbemessung der maximalen Momente an Zwischenauflagern und bei Einzelfundamenten zu verhindern, wurden Vorgehensweisen festgelegt, nach denen sie abgemindert werden dürfen.

Momentenabminderung an Zwischenauflagern

Da die idealisierten Auflager von Durchlaufträgern nicht der tatsächlichen Auflagerung entsprechen, darf eine Abminderung des rechnerischen Stützmomentes über die Auflagerbreite erfolgen. Die Momentenabminderung an Zwischenauflagern wird im EC2 Teil 1-1 Absatz 5.3.2.2 geregelt. Es wird unterschieden zwischen einer frei drehbaren Lagerung und einem monolithischen Anschluss.
Das rechnerische Stützmoment $|M_{\mathrm {Ed} }|$ darf um den Betrag $|\Delta M_{\mathrm {Ed} }|$ abgemindert werden, unter der Voraussetzung, dass bei der Berechnung der Stütztmomente die effektive Stützweite $l_{\mathrm {eff} }$ zwischen den Auflagermitten ermittelt wurde.

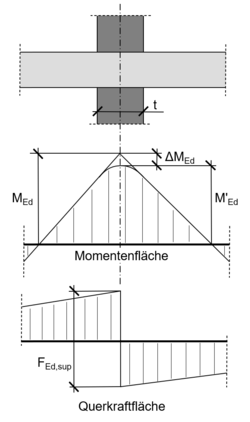
Abminderung bei frei drehbarer Lagerung

Abminderung des Stützmomentes bei einem frei drehbaren Zwischenauflager

Bei einer frei drehbaren Lagerung darf das Stützmoment parabelförmig über die Auflagerbreite ausgerundet werden. Die Abminderung des maximalen Stützmomentes wird aus der Auflagerkraft bzw. dem Querkraftsprung der tatsächlichen Auflagerbreite errechnet. Der maßgebende Bemessungsschnitt liegt dabei weiterhin in der Mitte des Auflagers. Ein Beispiel für ein frei drehbares Lager wäre die Auflagerung einer Decke auf einer Mauerwerkswand. Bei der Bemessung der Bauteile müssen die Mindestmomente eingehalten werden.

Das abgeminderte Moment berechnet sich nach folgenden Formeln:

${\begin{aligned}|\Delta M_{\mathrm {Ed} }|=|F_{\mathrm {Ed,sup} }|\cdot {\cfrac {t}{8}}\end{aligned}}$

${\begin{aligned}|M'_{\mathrm {Ed} }|=|M_{\mathrm {Ed} }|-|\Delta M_{\mathrm {Ed} }|\end{aligned}}$

wobei:

∆MEd ...	Abminderung des Stützmomentes
FEd,sup ...	Bemessungswert der Auflagerreaktion
t ...	Auflagerbreite
M'Ed ...	Abgemindertes Stützmoment
MEd ...	ideelles Spitzenmoment

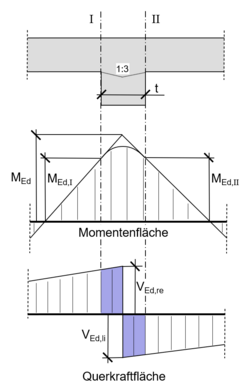
Abminderung bei einem monolithischen Anschluss

Abminderung des Stützmomentes bei einem monolithischen Anschluss zwischen Platte und Auflager

Bei einer monolithischen Verbindung zwischen Platte und Auflager darf das maßgebende Stützmoment am Rand der des Auflagers angenommen werden. Es wird das Moment über beiden Auflagerrändern ermittelt und mit dem Größeren weitergerechnet. Um das Moment am Auflagerrand zu erhalten wird das Spitzenmoment um die Querkraftfläche im Bereich des Auflagers (blau markierte Fläche im Bild) verringert. Die trapezförmige Fläche kann vereinfacht als Rechteck angenommen werden.
Das stützende Bauteil muss eine Vergrößerung der statischen Nutzhöhe von mindestens 1:3 (Neigung) zulassen. Ist die Nutzhöhenvergrößerung unter der Neigung nicht möglich, kann das ausgerundete Moment in Auflagermitte maßgebend werden. Ein Beispiel für einen monolithischen Anschluss wäre die indirekte Auflagerung einer Decke auf einen Stahlbetonunterzug. Bei der Bemessung der Bauteile müssen die Mindestmomente eingehalten werden.

Die abgeminderten Momente berechnen sich nach folgenden Formeln:

${\begin{aligned}|M_{\mathrm {Ed,I} }|=|M_{\mathrm {Ed} }|-|V_{\mathrm {Ed,li} }|\cdot {\cfrac {t}{2}}\end{aligned}}$

${\begin{aligned}|M_{\mathrm {Ed,II} }|=|M_{\mathrm {Ed} }|-|V_{\mathrm {Ed,re} }|\cdot {\cfrac {t}{2}}\end{aligned}}$

wobei:

MEd ...	ideelles Spitzenmoment
t ...	Auflagerbreite
MEd,I ...	Bemessungs-Stützmoment am linken Auflagerrand
MEd,II ...	Bemessungs-Stützmoment am rechten Auflagerrand
VEd,li ...	Bemessungsquerkraft am linken Auflagerrand
VEd,re ...	Bemessungsquerkraft am rechten Auflagerrand

Mindestmomente

Biegemomente M₀ an den Auflagerrändern bei Volleinspannung

Zur Berücksichtigung von Idealisierungen und unbeabsichtigten Abweichungen müssen Mindestwerte der Stützmomente eingehalten werden. Nach EC2 im Teil 1-1 Absatz 5.3.2.2 dürfen die Momente am Rand des Auflagers nicht kleiner sein als 65 % des Moments bei Annahme einer vollen Randeinspannung.

Daraus folgt:

${\begin{aligned}\min \,|M_{\mathrm {Ed} }|\geq 0,65\cdot M_{\mathrm {0} }\end{aligned}}$

wobei:

min MEd ...	Mindestbemessungsmoment
M0 ...	Volleinspannung am Auflagerrand mit der lichten Stützweite ln

Für eine gleichmäßig verteilte und konstante Streckenlast, erhält man folgende Formeln für das Mindestbemessungsmoment:

${\begin{aligned}\min \,|M_{\mathrm {Ed} }|\approx {\cfrac {F_{\mathrm {d} }\cdot l_{\mathrm {n} }^{2}}{12}}\end{aligned}}$ → an der ersten Innenstütze im Randfeld

${\begin{aligned}\min \,|M_{\mathrm {Ed} }|\approx {\cfrac {F_{\mathrm {d} }\cdot l_{\mathrm {n} }^{2}}{18}}\end{aligned}}$ → an den übrigen Innenstützen in Innenfeldern

wobei:

min MEd ...	Mindestbemessungsmoment
Fd ...	gleichmäßig verteilte Bemessungslast
ln ...	lichte Weite zwischen den Auflagern

Momentenabminderung bei Einzelfundamenten

Da die abzutragenden Kräfte über eine Stütze mit einer gewissen Breite in das Fundament eingeleitet werden, können ähnlich wie bei den Zwischenauflagern die Spitzenmomente abgemindert werden. Wichtig ist, dass die Vereinfachungen nur für zentrisch belastete Einzelfundamente gelten, da in den Berechnungsansätzen von einer gradlinigen Verteilung der Bodenpressung ausgegangen wird. Unterschieden wir hierbei zwischen der Abminderung bei nicht biegefesten und biegefesten Verbindungen zwischen Stütze und Fundament.

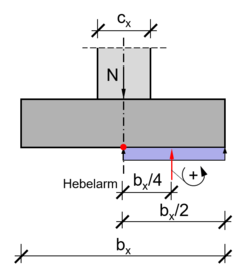
Ideelles Spitzenmoment

ideelles Spitzenmoment (rein theoretisch)

Bei der Berechnung des ideellen Spitzenmomentes wird die Breite der lasteinleitenden Stütze nicht berücksichtigt und das Moment im Fundament am idealisierten System berechnet.
Um die nachfolgenden Momentenabminderung besser verstehen zu können, wird die allgemeine Formel zur Bestimmung des maximalen Momentes hergeleitet:

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N}{b_{\mathrm {x} }}}\cdot {\cfrac {b_{\mathrm {x} }}{2}}\cdot {\cfrac {b_{\mathrm {x} }}{4}}\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N\cdot b_{\mathrm {x} }}{8}}\end{aligned}}$

wobei:

Mmax ...	maximales Spitzenmoment
N ...	Normalkraft aus der Stütze
bx ...	Fundamentbreite in x-Richtung

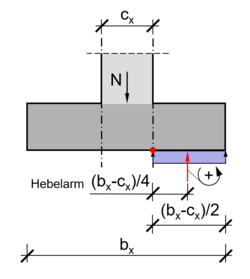
Im ersten Schritt sind die einzelnen Faktoren der zur Ermittlung des Spitzenmomentes aufgeführt und im Zweiten wird die Formel zusammengefasst. Der Bemessungsschnitt liegt in der Mitte des Fundamentes. Mit N/b_x wir die Normalkraft aus der Stütze auf die Fundamentbreite verteilt, sodass man die Bodenpressung erhält. Danach wird die verteilte Normalkraft mit der halben Fundamentbreite b_x/2 multipliziert, um die resultierende Kraft zu erhalten, die das maximale Moment erzeugt (roter Pfeil im Bild). Um das Moment zu erhalten, muss noch mit dem Hebelarm b_x/4 multipliziert werden.

Ausrundungsmoment bei einer nicht biegefesten Verbindung zwischen Stütze und Fundament

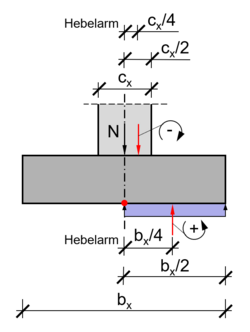
Ausrundungsmoment bei einer nicht biegefesten Verbindung zwischen Stütze und Fundament

Handelt es sich um eine nicht biegefeste Verbindung zwischen Stütze und Einzelfundament (es können keine Biegemomente aus der Stütze in das Fundament übertragen werden), darf das Ausrundungsmoment ermittelt werden. Bei der Berechnung wird nicht mehr nur eine Einzellast angesetzt, sondern die Normalkräfte werden gleichmäßig über die Stützbreite verteilt. Der Bemessungsschnitt liegt dabei weiterhin in der Mitte des Fundamentes und der Stütze.

Das Ausrundungsmoment wird aus folgenden Formeln hergeleitet:

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N}{b_{\mathrm {x} }}}\cdot {\cfrac {b_{\mathrm {x} }}{2}}\cdot {\cfrac {b_{\mathrm {x} }}{4}}-{\cfrac {N}{c_{\mathrm {x} }}}\cdot {\cfrac {c_{\mathrm {x} }}{2}}\cdot {\cfrac {c_{\mathrm {x} }}{4}}\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N\cdot b_{\mathrm {x} }}{8}}-{\cfrac {N\cdot c_{\mathrm {x} }}{8}}\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N}{8}}\cdot \left(b_{\mathrm {x} }-c_{\mathrm {x} }\right)\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N\cdot b_{\mathrm {x} }}{8}}\cdot \left(1-{\cfrac {b_{\mathrm {x} }}{c_{\mathrm {x} }}}\right)\end{aligned}}$

wobei:

Mmax ...	maximales Ausrundungsmoment
N ...	Normalkraft aus der Stütze
bx ...	Fundamentbreite in x-Richtung
cx ...	Stützenbreite in x-Richtung

Der Unterschied zur Ermittlung des ideellen Spitzenmoments liegt in der Berücksichtigung der Auflagerbreite. Es entsteht eine zweite resultierende Kraft aus der Verteilung der Normalkräfte über die Breite der Stütze, welche dem Moment aus der Boddenpressung entgegenwirkt. Dadurch wird das maximale Moment im Fundament kleiner und somit ausgerundet. Das entgegengesetzt drehende Moment berechnet sich analog zu dem aus der Sohlpressung. Die Normalkraft wird über die Breite verteilt N/c_x, dann mit der halben Stützenbreite b_x/2 und dem Hebelarm c_x/4 multipliziert. Die Formel wird in mehreren Schritten vereinfacht und umgestellt, um auf die Schreibweise aus dem Heft 631 des Deutschen Ausschusses für Stahlbetonbau (kurz: DAfStb) zu kommen.

Anschnittmoment bei einer biegefesten Verbindung zwischen Stütze und Fundament

Anschnittsmoment bei einer biegefesten Verbindung zwischen Stütze und Fundament

Wenn die Stütze und das Einzelfundament monolithisch miteinander verbunden sind, dann können Biegemomente aus der Stütze in das Fundament übertragen werden und es darf das Anschnittmoment ermittelt werden. Aufgrund der biegefesten Verbindung und der daraus folgenden höheren Steifigkeit sind die Krümmungen direkt im Stützenbereich so gering, dass sie für die Bemessung nicht mehr maßgebend sind. Dabei rutscht der Berechnungsschnitt an die beiden Ränder der Stütze.

Das Anschnittmoment wird aus folgenden Formeln hergeleitet:

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N}{b_{\mathrm {x} }}}\cdot {\cfrac {(b_{\mathrm {x} }-c_{\mathrm {x} })}{2}}\cdot {\cfrac {(b_{\mathrm {x} }-c_{\mathrm {x} })}{4}}\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N}{b_{\mathrm {x} }\cdot 8}}\cdot \left(b_{\mathrm {x} }^{2}-2\cdot b_{\mathrm {x} }\cdot c_{\mathrm {x} }+c_{\mathrm {x} }^{2}\right)\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N\cdot b_{\mathrm {x} }}{8}}\cdot \left(1-2\cdot {\cfrac {c_{\mathrm {x} }}{b_{\mathrm {x} }}}+{\cfrac {c_{\mathrm {x} }^{2}}{b_{\mathrm {x} }^{2}}}\right)\end{aligned}}$

${\begin{aligned}M_{\mathrm {max} }={\cfrac {N\cdot b_{\mathrm {x} }}{8}}\cdot \left(1-{\cfrac {b_{\mathrm {x} }}{c_{\mathrm {x} }}}\right)^{2}\end{aligned}}$

wobei:

Mmax ...	maximales Anschnittmoment
N ...	Normalkraft aus der Stütze
bx ...	Fundamentbreite in x-Richtung
cx ...	Stützenbreite in x-Richtung

Da der Bemessungsschnitt im Anschnittsbereich liegt, erzeugt nur noch der Sohldruck links und rechts von der Stütze ein Moment. Die Formel setzt sich aus den selben Gleichgewichtsbedingungen wie beim Ausrundungsmoment zusammen. Nur die Abstände müssen anders ermittelt werden, da sich der Schnitt verschoben hat. Die Formel wird wieder in mehreren Schritten vereinfacht, um auf die Schreibweise aus dem Heft 631 (DAfSbt) zu kommen.

Quellen

Seiteninfo Status: Seite fertig, ungeprüft