Brandschutznachweis Stahlbetonstütze (Bsp.): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | + | == Methode A (Tafel) == | |
| − | + | === Gegeben: === | |
| − | |||
Stahlbetonpendelstütze:<br /> | Stahlbetonpendelstütze:<br /> | ||
- unverschieblich<br /> | - unverschieblich<br /> | ||
| Zeile 9: | Zeile 8: | ||
- gefordert: R60<br /> | - gefordert: R60<br /> | ||
| − | + | === Einwirkungen === | |
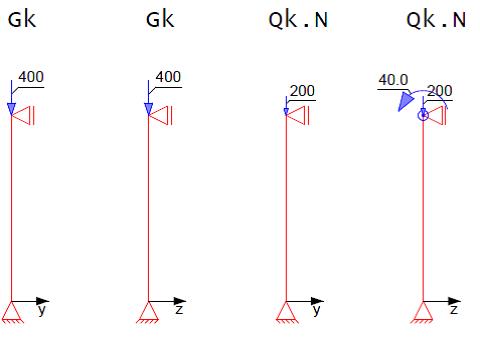
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 1.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br /> | [[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 1.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br /> | ||
<br /> | <br /> | ||
| − | + | === Querschnitts- und Systemabmessungen === | |
<math>\begin{array}{l}b/h=30/30\\l=3m\\\frac{{{d}_{1}}}{h}=\frac{0,054}{0,3}=0,18\approx 0,2\end{array}</math> | <math>\begin{array}{l}b/h=30/30\\l=3m\\\frac{{{d}_{1}}}{h}=\frac{0,054}{0,3}=0,18\approx 0,2\end{array}</math> | ||
| Zeile 19: | Zeile 18: | ||
auf sichere Seite gerundet | auf sichere Seite gerundet | ||
| − | + | === Schnittgrößen === | |
<math>\begin{array}{l}{{N}_{Ed}}=1,35\cdot 400+1,5\cdot 200=840kN\\{{M}_{Ed}}=66,3kNm\end{array}</math> | <math>\begin{array}{l}{{N}_{Ed}}=1,35\cdot 400+1,5\cdot 200=840kN\\{{M}_{Ed}}=66,3kNm\end{array}</math> | ||
| Zeile 25: | Zeile 24: | ||
ohne Rechnung, einschließlich Theorie II. Ordnung | ohne Rechnung, einschließlich Theorie II. Ordnung | ||
| − | + | === Kaltbemessung: bezogene Schnittgrößen === | |
<math>\begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-840}{30\cdot 30\cdot 0,85\cdot \frac{2,0}{1,5}}=-0,82\\{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{6630}{30\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,0}{1,5}}=0,22\end{array}</math> | <math>\begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-840}{30\cdot 30\cdot 0,85\cdot \frac{2,0}{1,5}}=-0,82\\{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{6630}{30\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,0}{1,5}}=0,22\end{array}</math> | ||
| − | + | === Kaltbemessung: Interaktionsdiagramm === | |
Ermittlung des mechanischen Bewehrungsgrades, <math>{{\omega }_{tot}}=0,56~</math> | Ermittlung des mechanischen Bewehrungsgrades, <math>{{\omega }_{tot}}=0,56~</math> | ||
| Zeile 36: | Zeile 35: | ||
gewählt: 2x 6ø12, <math>{{A}_{s}}=13,57cm{}^\text{2}~</math> | gewählt: 2x 6ø12, <math>{{A}_{s}}=13,57cm{}^\text{2}~</math> | ||
| − | + | === Heißbemessung: Bedingungen === | |
- Bewehrungsgrad <math>\frac{13,57}{30\cdot 30}=0,015\le 0,04</math> | - Bewehrungsgrad <math>\frac{13,57}{30\cdot 30}=0,015\le 0,04</math> | ||
| Zeile 43: | Zeile 42: | ||
Bemessung nach Tafel legitimiert. | Bemessung nach Tafel legitimiert. | ||
| − | + | === Heißbemessung: Außergewöhnliche Einwirkungskombination während des Brandfalls === | |
<math>{{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN</math> | <math>{{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN</math> | ||
| − | + | === Heißbemessung: Ermittlung des Reduktionsfaktors === | |
<math>{{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62</math> | <math>{{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62</math> | ||
| − | + | === Heißbemessung: Bezogene Schnittgrößen === | |
(vereinfacht mit <math>0,62\cdot {{\nu }_{Ed}}</math> oder genauer mit <math>{{\alpha }_{cc}}=1,0~</math>): | (vereinfacht mit <math>0,62\cdot {{\nu }_{Ed}}</math> oder genauer mit <math>{{\alpha }_{cc}}=1,0~</math>): | ||
<math>\begin{array}{l}{{\nu }_{Ed,fi,t}}=\frac{{{N}_{Ed,fi}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-520}{30\cdot 30\cdot \frac{2,0}{1,5}}=-0,43\\{{\mu }_{Ed,fi,t}}=\frac{{{M}_{Ed,fi}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{0,62\cdot 6630}{30\cdot 30{}^\text{2}\cdot \frac{2,0}{1,5}}=0,11\end{array}</math> | <math>\begin{array}{l}{{\nu }_{Ed,fi,t}}=\frac{{{N}_{Ed,fi}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-520}{30\cdot 30\cdot \frac{2,0}{1,5}}=-0,43\\{{\mu }_{Ed,fi,t}}=\frac{{{M}_{Ed,fi}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{0,62\cdot 6630}{30\cdot 30{}^\text{2}\cdot \frac{2,0}{1,5}}=0,11\end{array}</math> | ||
| − | + | === Heißbemessung: Mechanischer Bewehrungsgrad === | |
bei Berücksichtigung von <math>{{\alpha }_{cc}}=1,0~</math>: | bei Berücksichtigung von <math>{{\alpha }_{cc}}=1,0~</math>: | ||
<math>{{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/\frac{2,0}{1,5} \right)}{30\cdot 30}=0,49</math> | <math>{{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/\frac{2,0}{1,5} \right)}{30\cdot 30}=0,49</math> | ||
| − | + | === Heißbemessung: Ermittlung der zulässigen bezogenen Normalkraft mithilfe des Interaktionsdiagramms === | |
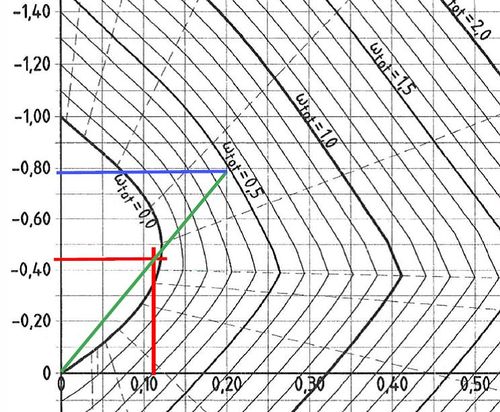
[[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 2.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br /> | [[File:Brandschutznachweis Stahlbetonstütze (Bsp.) 2.jpg|rahmenlos|rand|tumb|500px|Baustatik-Wiki]]<br /> | ||
<br /> | <br /> | ||
| Zeile 87: | Zeile 86: | ||
Eine Nachweisführung mit Methode B kann in diesem Fall nicht erfolgen, weil die Stütze eine Schlankheit von 30 als Bedingung übersteigt. | Eine Nachweisführung mit Methode B kann in diesem Fall nicht erfolgen, weil die Stütze eine Schlankheit von 30 als Bedingung übersteigt. | ||
| − | + | == Methode A (Gleichung) == | |
| + | Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A).<br /> | ||
| + | Die Vorgehensweise zu Ermittlung des Ausnutzungsgrades ist dieselbe. | ||
| − | === | + | === Mechanischer Bewehrungsgrad === |
| − | = | + | <math>{{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/0,85\cdot \frac{2,0}{1,5} \right)}{30\cdot 30}=0,58</math> |
| − | |||
| − | === | + | === Ermittlung der Summanden === |
| − | === Methode B === | + | <math>\begin{array}{l}{{R}_{\eta ,fi}}=83\cdot \left( 1-{{\mu }_{fi}}\cdot \frac{1+\omega }{(0,85/{{\alpha }_{cc}})+\omega } \right)=83\cdot \left( 1-0,55\cdot \frac{1+0,58}{(0,85/1)+0,58} \right)=32,56\\{{R}_{a}}=1,6\cdot (a-30)=1,6\cdot \left( 54-30 \right)=38,4\\{{R}_{l}}=9,6\cdot (5-{{l}_{0,fi}})=9,6\cdot (5-3)=19,2\\{{R}_{b}}=0,09\cdot b'=0,09\cdot \frac{2\cdot {{A}_{c}}}{b+h}=0,09\cdot \frac{2\cdot (300{}^\text{2}-1357)}{300+300}=26,59\\{{R}_{n}}=12\end{array}</math> |
| + | |||
| + | === Ermittlung der Branddauer === | ||
| + | |||
| + | <math>R=120\cdot {{\left( \frac{{{R}_{\eta ,fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}=120\cdot {{\left( \frac{32,56+38,4+19,2+26,59+12}{120} \right)}^{1,8}}=136\min </math> | ||
| + | <br /><br /> | ||
| + | Nachweis erfüllt. | ||
| + | |||
| + | == Methode B == | ||
| + | Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A). Die Länge wird hier mit <math>l=2,5m</math> vorgegeben. Das Moment nach Theorie II. Ordnung ergibt sich zu <math>{{M}_{Ed,2}}=65,25kNm</math>. | ||
| + | |||
| + | === Mechanischer Bewehrungsgrad === | ||
| + | |||
| + | <math>\omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{13,57\cdot \frac{50}{1,15}}{\left( {{30}^{2}}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}}=0,59a</math> | ||
| + | |||
| + | === Außergewöhnliche Einwirkungskombination während des Brandfalls === | ||
| + | |||
| + | <math>{{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN</math> | ||
| + | |||
| + | === Ermittlung des Reduktionsfaktors === | ||
| + | |||
| + | <math>{{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62</math> | ||
| + | |||
| + | === Ermittlung des Ausnutzungsgrades === | ||
| + | |||
| + | <math>n=\frac{{{N}_{Ed,fi}}}{0,7\cdot \left( {{A}_{c}}\cdot {{f}_{cd}}+{{A}_{s}}\cdot {{f}_{yd}} \right)}=\frac{520}{0,7\cdot \left[ \left( 30{}^\text{2}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}+13,57\cdot \frac{50}{1,15} \right]}=0,47</math> | ||
| + | |||
| + | === Zulässige Knicklänge === | ||
| + | |||
| + | <math>{{\lambda }_{fi,t}}=\frac{{{l}_{0,fi}}}{i}=\frac{{{l}_{0,fi}}}{\sqrt{\frac{I}{A}}}=\frac{250}{\sqrt{\frac{{{30}^{4}}/12}{{{30}^{2}}}}}=28,87\le 30</math> | ||
| + | |||
| + | === Zulässige Ausmitte === | ||
| + | |||
| + | <math>e=\frac{{{M}_{0,Ed,fi}}}{{{N}_{Ed,fi}}}=\frac{0,62\cdot 65,25}{520}=0,079m>b\cdot 0,25=0,075m</math> | ||
| + | <br /><br /> | ||
| + | Bedingung nicht erfüllt, ein Eingang in die Tafel ist hinfällig. | ||
Version vom 18. September 2015, 14:14 Uhr
Methode A (Tafel)
Gegeben:
Stahlbetonpendelstütze:
- unverschieblich
- beidseitig gelenkig gelagert
- Nutzung als Verkaufsraum
- allseitig beflammt
- gefordert: R60
Einwirkungen
Querschnitts- und Systemabmessungen
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\begin{array}{l}b/h=30/30\\l=3m\\{\frac {{d}_{1}}{h}}={\frac {0,054}{0,3}}=0,18\approx 0,2\end{array}}}
auf sichere Seite gerundet
Schnittgrößen
ohne Rechnung, einschließlich Theorie II. Ordnung
Kaltbemessung: bezogene Schnittgrößen
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {\begin{array}{l}{{\nu }_{Ed}}={\frac {{N}_{Ed}}{b\cdot h\cdot {{f}_{cd}}}}={\frac {-840}{30\cdot 30\cdot 0,85\cdot {\frac {2,0}{1,5}}}}=-0,82\\{{\mu }_{Ed}}={\frac {{M}_{Ed}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}}={\frac {6630}{30\cdot 30{}^{\text{2}}\cdot 0,85\cdot {\frac {2,0}{1,5}}}}=0,22\end{array}}}
Kaltbemessung: Interaktionsdiagramm
Ermittlung des mechanischen Bewehrungsgrades,
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{A}_{s}}={{\omega }_{tot}}\cdot {\frac {b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}}=0,56\cdot {\frac {0,3\cdot 0,3}{{\frac {50}{1,15}}/\left(0,85\cdot {\frac {2}{1,5}}\right)}}=13,09cm{}^{\text{2}}}
gewählt: 2x 6ø12, Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{A}_{s}}=13,57cm{}^{\text{2}}~}
Heißbemessung: Bedingungen
- Bewehrungsgrad
- Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{l}_{0,fi}}=3\leq 3}
Bemessung nach Tafel legitimiert.
Heißbemessung: Außergewöhnliche Einwirkungskombination während des Brandfalls
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN}
Heißbemessung: Ermittlung des Reduktionsfaktors
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62}
Heißbemessung: Bezogene Schnittgrößen
(vereinfacht mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,62\cdot {{\nu }_{Ed}}} oder genauer mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc}}=1,0~} ):
Heißbemessung: Mechanischer Bewehrungsgrad
bei Berücksichtigung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc}}=1,0~} :
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/\frac{2,0}{1,5} \right)}{30\cdot 30}=0,49}
Heißbemessung: Ermittlung der zulässigen bezogenen Normalkraft mithilfe des Interaktionsdiagramms
Vom Diagrammnullpunkt über den Schnittpunkt der bezogenen heißbemessenen Schnittgrößen wird der mechanische Bewehrungsgrad angezielt und damit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu }_{Ed,fi,t,zul}}=-0,79~}
abgelesen.
Der Bemessungswiderstand der Normalkraft ergibt sich durch Wiedereinführen der Abmessungen:
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{N}_{Rd}}={{\nu }_{Ed,fi,t,zul}}\cdot b\cdot h\cdot {{f}_{cd}}=-0,79\cdot 30\cdot 30\cdot {\frac {2}{1,5}}=-948kN}
Das Verhältnis aus Einwirkung und Widerstand ergibt den Ausnutzungsgrad
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{fi}}=\frac{{{N}_{Ed,fi,t}}}{{{N}_{Rd}}}=\frac{-520}{-948}=0,55}
Durch Interpolation ergeben sich in der Tafel des Eurocode 2 für Methode A mit geforderter Brandwiderstandsdauer von 60 Minuten die folgenden Mindestabmessungen und Achsabstände:
212,5mm/38,5mm oder 312,5mm/33,25mm
Stütze mit 300mm/54mm eingehalten, Nachweis erfüllt.
Anmerkungen:
In der Vergleichsrechnung mit dem Modul S402.de wird die „kalte“ Einwirkungskombination mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{G,\inf }}}
, jedoch auch mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{Q,\sup }}}
berechnet. Weiterhin ist der Bemessungswert der „heißen“ Einwirkungskombination nicht nachzuvollziehen. Als Konsequenz ergibt sich ein höherer Ausnutzungsfaktor und eine entsprechend höhere Forderung zum Einhalten der Forderung R60.
Eine Nachweisführung mit Methode B kann in diesem Fall nicht erfolgen, weil die Stütze eine Schlankheit von 30 als Bedingung übersteigt.
Methode A (Gleichung)
Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A).
Die Vorgehensweise zu Ermittlung des Ausnutzungsgrades ist dieselbe.
Mechanischer Bewehrungsgrad
Ermittlung der Summanden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{R}_{\eta ,fi}}=83\cdot \left( 1-{{\mu }_{fi}}\cdot \frac{1+\omega }{(0,85/{{\alpha }_{cc}})+\omega } \right)=83\cdot \left( 1-0,55\cdot \frac{1+0,58}{(0,85/1)+0,58} \right)=32,56\\{{R}_{a}}=1,6\cdot (a-30)=1,6\cdot \left( 54-30 \right)=38,4\\{{R}_{l}}=9,6\cdot (5-{{l}_{0,fi}})=9,6\cdot (5-3)=19,2\\{{R}_{b}}=0,09\cdot b'=0,09\cdot \frac{2\cdot {{A}_{c}}}{b+h}=0,09\cdot \frac{2\cdot (300{}^\text{2}-1357)}{300+300}=26,59\\{{R}_{n}}=12\end{array}}
Ermittlung der Branddauer
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=120\cdot {{\left( \frac{{{R}_{\eta ,fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}=120\cdot {{\left( \frac{32,56+38,4+19,2+26,59+12}{120} \right)}^{1,8}}=136\min }
Nachweis erfüllt.
Methode B
Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A). Die Länge wird hier mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l=2,5m} vorgegeben. Das Moment nach Theorie II. Ordnung ergibt sich zu Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{M}_{Ed,2}}=65,25kNm} .
Mechanischer Bewehrungsgrad
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{13,57\cdot \frac{50}{1,15}}{\left( {{30}^{2}}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}}=0,59a}
Außergewöhnliche Einwirkungskombination während des Brandfalls
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN}
Ermittlung des Reduktionsfaktors
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62}
Ermittlung des Ausnutzungsgrades
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle n={\frac {{N}_{Ed,fi}}{0,7\cdot \left({{A}_{c}}\cdot {{f}_{cd}}+{{A}_{s}}\cdot {{f}_{yd}}\right)}}={\frac {520}{0,7\cdot \left[\left(30{}^{\text{2}}-13,57\right)\cdot 0,85\cdot {\frac {2}{1,5}}+13,57\cdot {\frac {50}{1,15}}\right]}}=0,47}
Zulässige Knicklänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{fi,t}}=\frac{{{l}_{0,fi}}}{i}=\frac{{{l}_{0,fi}}}{\sqrt{\frac{I}{A}}}=\frac{250}{\sqrt{\frac{{{30}^{4}}/12}{{{30}^{2}}}}}=28,87\le 30}
Zulässige Ausmitte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e=\frac{{{M}_{0,Ed,fi}}}{{{N}_{Ed,fi}}}=\frac{0,62\cdot 65,25}{520}=0,079m>b\cdot 0,25=0,075m}
Bedingung nicht erfüllt, ein Eingang in die Tafel ist hinfällig.