Durchstanzen - Besonderheiten von Fundamenten: Unterschied zwischen den Versionen
Mwulf (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „===Besonderheiten von Fundamenten ohne Durchstanzbewehrung=== Genauere Informationen zu Stützenkopfverstärkungen: [[Durchstanzen (Besonderheiten von Fundame…“) |
Mwulf (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
===Besonderheiten von Fundamenten ohne Durchstanzbewehrung=== | ===Besonderheiten von Fundamenten ohne Durchstanzbewehrung=== | ||
| − | |||
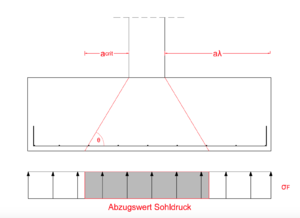
Bei Bodenplatten und Stützenfundamenten darf in der Fläche <math>A_{crit}</math> die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden. Durch die Bodenpressung und eine geringere Schubschlankheit fällt der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dieser Parameter ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt <ref name="Q9" >Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchtanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009</ref>.<br /> | Bei Bodenplatten und Stützenfundamenten darf in der Fläche <math>A_{crit}</math> die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden. Durch die Bodenpressung und eine geringere Schubschlankheit fällt der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dieser Parameter ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt <ref name="Q9" >Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchtanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009</ref>.<br /> | ||
Version vom 7. März 2016, 09:24 Uhr
Besonderheiten von Fundamenten ohne Durchstanzbewehrung
Bei Bodenplatten und Stützenfundamenten darf in der Fläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{crit}}
die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden. Durch die Bodenpressung und eine geringere Schubschlankheit fällt der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dieser Parameter ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt [1].
Die reduzierte Querkraftbeanspruchung ermittelt sich wie folgt:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed, red}=V_{Ed}-\Delta V_{Ed}}
Dabei stellt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed}}
den resultierenden Sohldruck der kritischen Fläche ohne das Fundamenteigengewicht dar.
Der im Vornherein unbekannte Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{crit}}
lässt sich wie folgt ermitteln (NA):
- gedrungene Fundamente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda \le 2,0 } : interactive Ermittlung des kritischen Rundschnitts
- schlanke Fundamente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda >2,0} : konstanter Rundschnitt im Abstand 1,0d.
mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda=\frac{a_{\lambda}}{d}}
und der Bedingung:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{crit}\le 2d}
Bei Fundamenten ohne vorherrschende Normalspannung und somit einem
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{cp} = 0} , wird der Nachweis wie folgt geführt:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed}\le\nu_{Rd}=C_{Rd,c}\cdot k\cdot (100\cdot f_{ck})^{1/3}\cdot\frac{2d}{a_{crit}}\ge\nu_{min}\cdot\frac{2d}{a_{crit}}} (NA)
Da bei Fundamenten ein Einfluss der Schlankheit vorherrscht, wird das geforderte Zuverlässigkeitsniveau nicht erreicht, folglich muss die Gleichung angepasst werden [2]:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_{Rd,c}=0,15/\gamma_c}
mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_c=1,5}
Die Einwirkung setzt sich hierbei folgendermaßen zusammen:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed}=\beta\cdot\frac{V_{Ed,red}}{u_{crit\cdot d}}}
mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta\le 1,10 } (NA)
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta= 1,10 }
(NA) für mittige Belastung
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta= 1+k\cdot\frac{M_{Ed}\cdot u_{crit}}{V_{Ed,red}\cdot W}}
für aussermittige Belastung
Es besteht somit eine Analogie zwischen dem Nachweis der Durchstanztragfähigkeit
und der Ermittlung der Querkrafttragfähigkeit bei biegebewehrten Stahlbetonbauteilen.
Da durch den rotationssymmetrischen Durchstanzkegel eine höhere Rissverzahnung vorliegt, fällt die Durchstanztragfähigkeit jedoch höher aus [3].
Ermittlung des Abstandes acrit
In Abhängigkeit des Abstandes acrit kann mit der folgenden Gleichung das maßgebende Minimum ermittelt werden. Somit ergibt sich der relevante kritische Rundschnitt.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{V_{Rd,c}}{1-\frac{A_{cont}}{A_F}}}
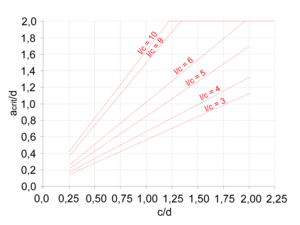
Neben der aufwendigen iterativen Methode zur Ermittlung von acrit bietet das aufgezeigte Diagramm (siehe Bild 15) eine alternative Bestimmungsoption. Dieses stellt die Zusammenhänge der folgenden Eingangsparameter dar [4]:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{c}{d} und \frac{l}{c}}
mit
l- Fundamentlänge
c- Stützenbreite
d- statische Nutzhöhe
Ausmittig belastete Fundamente mit klaffenden Fugen im Rundschnittbereich
In diesem Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (e = l/6)}
sollte die Berechnung über einzelne Sektoren erfolgen. Der abzuziehende Wert für den Sohldruck ergibt sich somit für jeden Sektor separat [5].
- ↑ Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchtanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009
- ↑ Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
- ↑ Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012.
- ↑ Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012
- ↑ G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010