Bemessungsmoment am Anschnitt (Bsp.): Unterschied zwischen den Versionen
Aklemm (Diskussion | Beiträge) |
Aklemm (Diskussion | Beiträge) |
||
| Zeile 9: | Zeile 9: | ||
==Beispiel 1 <small>Bemessungsmomente für monolithische Auflager</small>== | ==Beispiel 1 <small>Bemessungsmomente für monolithische Auflager</small>== | ||
| − | Das folgende Beispiel zeigt eine manuelle Berechnung der Bemessungsmomente am Anschnitt der monolithischen Auflager, verglichen mit den [[Ermittlung der Bemessungsmomente (S340.de)#Bemessung am Anschnitt|Bemessungsmomenten]], welche von dem Modul S340.de ausgegeben werden. Desweiteren werden die Bemessungsmomente von dem Modul S340.de mit den [[Ermittlung der Bemessungsmomente (S340.de)#Mindestmoment am Innenauflager|Mindestmomenten]] berechnet nach den Regeln vom Modul S340.de- gegenüber gestellt und bewertet. | + | Das folgende Beispiel zeigt eine manuelle Berechnung der Bemessungsmomente am Anschnitt der monolithischen Auflager, verglichen mit den [[Ermittlung der Bemessungsmomente (S340.de)#Bemessung am Anschnitt|Bemessungsmomenten]], welche von dem Modul S340.de ausgegeben werden. Desweiteren werden die Bemessungsmomente von dem Modul S340.de mit den [[Ermittlung der Bemessungsmomente (S340.de)#Mindestmoment am Innenauflager|Mindestmomenten]] -berechnet nach den Regeln vom Modul S340.de- gegenüber gestellt und bewertet. |
===Aufgabe=== | ===Aufgabe=== | ||
Ermittlung des Bemessungsmoment über einer frei drehbaren Lagerung für einen Stahlbetondeckenplatte mit folgendem System:<br /> | Ermittlung des Bemessungsmoment über einer frei drehbaren Lagerung für einen Stahlbetondeckenplatte mit folgendem System:<br /> | ||
Version vom 31. März 2016, 17:04 Uhr
| Hauptseite • Stahlbetonbau • Beispiele • Hinweise für Leser • Hinweise für Autoren |
Beispiel 1 Bemessungsmomente für monolithische Auflager
Das folgende Beispiel zeigt eine manuelle Berechnung der Bemessungsmomente am Anschnitt der monolithischen Auflager, verglichen mit den Bemessungsmomenten, welche von dem Modul S340.de ausgegeben werden. Desweiteren werden die Bemessungsmomente von dem Modul S340.de mit den Mindestmomenten -berechnet nach den Regeln vom Modul S340.de- gegenüber gestellt und bewertet.
Aufgabe
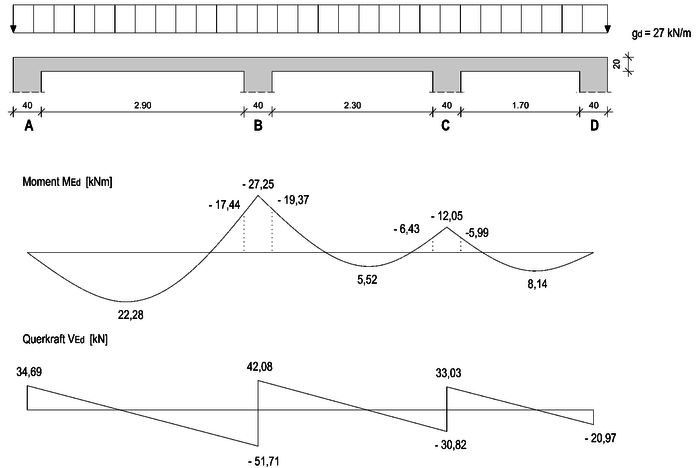
Ermittlung des Bemessungsmoment über einer frei drehbaren Lagerung für einen Stahlbetondeckenplatte mit folgendem System:
Vorgabewerte
Schnittgrößen wurden aus einer Rechnung von dem Modul S340.de übernommen:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B}=-27{,}25\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B,li}=-17{,}44\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,B,re}=-19{,}37\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,B,li}=-51{,}71\,\mathrm{kN}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,B,re}=42{,}08\,\mathrm{kN}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,C}=-12{,}05\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,C,li}=-6{,}43\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle M_\mathrm{Ed,C,re}=-5{,}99\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,C,li}=-30{,}82\,\mathrm{kN}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_\mathrm{Ed,C,re}=33{,}03\,\mathrm{kN}}
Auflagerbreite:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t=0{,}40\,\mathrm{m}}
Deckenstärke:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h=0{,}20\,\mathrm{m}}
Berechnung
Bemessung am Anschnitt von Auflager B
manuelle Berechnung der Momente am Anschnitt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=\vert M_\mathrm{Ed}\vert - \vert V_\mathrm{Ed,li}\vert \cdot \cfrac{t}{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=27{,}25\,\mathrm{kNm} - 51{,}71\,\mathrm{kN} \cdot \cfrac{0{,}40\,\mathrm{m}}{2}=16{,}91\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=\vert M_\mathrm{Ed}\vert - \vert V_\mathrm{Ed,re}\vert \cdot \cfrac{t}{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=27{,}25\,\mathrm{kNm} - 42{,}08\,\mathrm{kN} \cdot \cfrac{0{,}40\,\mathrm{m}}{2}=18{,}83\,\mathrm{kNm}}
- Die manuelle Berechnung ist nur eine Näherung, die vom Modul S340.de nicht beachtet wird, da das Programm die Schnittgrößen an den Anschnitten genau ermitteln kann.
Anschnittmoment ermittelt vom Modul S340.de nach linear-elastischer Schnittgrößenermittlung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=\underline{17{,}44\,\mathrm{kNm}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=\underline{19{,}37\,\mathrm{kNm}}}
Mindestmoment
Mindestmoment als Innenstütze im Randfeld:
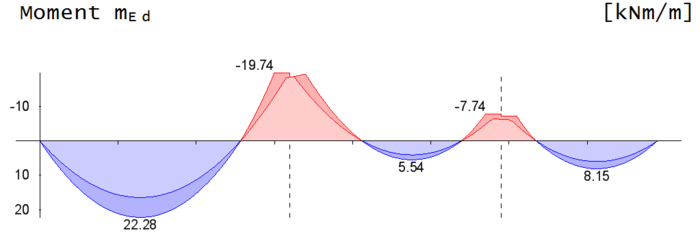
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Rand}\vert=0{,}65\cdot \cfrac{(g_\mathrm{d} + q_\mathrm{d})\cdot (l_\mathrm{n}\cdot a_\mathrm{i})^{~2}}{8}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i}=\mathrm{min} \{ 0{,}5\cdot t~;~0{,}5\cdot h \}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i}= 0{,}5\cdot 0{,}20\,\mathrm{m}=0{,}10\,\mathrm{m}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Rand}\vert=0{,}65\cdot \cfrac{27\,\mathrm{kN}\mathrm{m}^{-1}\cdot (3{,}00\,\mathrm{m})^{~2}}{8}=\underline{\underline{19{,}74\,\mathrm{kNm}}}~~~\mathrm{massgebend}}
Mindestmoment als Innenstütze im Innenfeld:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Innen}\vert=0{,}65\cdot \cfrac{(g_\mathrm{d} + q_\mathrm{d})\cdot l_\mathrm{n}^{~2}}{12}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Innen}\vert=0{,}65\cdot \cfrac{27\,\mathrm{kN}\mathrm{m}^{-1}\cdot (2{,}30\,\mathrm{m})^{~2}}{12}=\underline{7{,}74\,\mathrm{kNm}}}
Bemessung am Anschnitt von Auflager C
manuelle Berechnung der Momente am Anschnitt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=\vert M_\mathrm{Ed}\vert - \vert V_\mathrm{Ed,li}\vert \cdot \cfrac{t}{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=12{,}05\,\mathrm{kNm} - 30{,}82\,\mathrm{kN} \cdot \cfrac{0{,}40\,\mathrm{m}}{2}=5{,}89\,\mathrm{kNm}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=\vert M_\mathrm{Ed}\vert - \vert V_\mathrm{Ed,re}\vert \cdot \cfrac{t}{2}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=12{,}05\,\mathrm{kNm} - 33{,}03\,\mathrm{kN} \cdot \cfrac{0{,}40\,\mathrm{m}}{2}=5{,}44\,\mathrm{kNm}}
- Die manuelle Berechnung ist nur eine Näherung, die vom Modul S340.de nicht beachtet wird, da das Programm die Schnittgrößen an den Anschnitten genau ermitteln kann.
Anschnittmoment ermittelt vom Modul S340.de nach linear-elastischer Schnittgrößenermittlung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,I}\vert=\underline{6{,}43\,\mathrm{kNm}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vert M_\mathrm{Ed,II}\vert=\underline{5{,}99\,\mathrm{kNm}}}
Mindestmoment
Mindestmoment als Innenstütze im Innenfeld:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Innen}\vert=0{,}65\cdot \cfrac{(g_\mathrm{d} + q_\mathrm{d})\cdot l_\mathrm{n}^{~2}}{12}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Innen}\vert=0{,}65\cdot \cfrac{27\,\mathrm{kN}\mathrm{m}^{-1}\cdot (2{,}30\,\mathrm{m})^{~2}}{12}=\underline{\underline{7{,}74\,\mathrm{kNm}}}~~~\mathrm{massgebend}}
Mindestmoment als Innenstütze im Randfeld:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Rand}\vert=0{,}65\cdot \cfrac{(g_\mathrm{d} + q_\mathrm{d})\cdot (l_\mathrm{n}\cdot a_\mathrm{i})^{~2}}{8}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i}=\mathrm{min} \{ 0{,}5\cdot t~;~0{,}5\cdot h \}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i}= 0{,}5\cdot 0{,}20\,\mathrm{m}=0{,}10\,\mathrm{m}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{min}\vert M_\mathrm{Ed,Rand}\vert=0{,}65\cdot \cfrac{27\,\mathrm{kN}\mathrm{m}^{-1}\cdot (1{,}80\,\mathrm{m})^{~2}}{8}=\underline{7{,}11\,\mathrm{kNm}}}
Vergleich mit mb-AEC Baustatik
In der Ausgabe vom Modul S340.de, erscheint folgender Ausdruck:
Seiteninfo
|