Stahlbetonstütze - Verfahren mit Nennkrümmung: Unterschied zwischen den Versionen
Gast (Diskussion | Beiträge) |
Gast (Diskussion | Beiträge) |
||
| Zeile 19: | Zeile 19: | ||
<br /> | <br /> | ||
| − | Das Modellstützenverfahren eignet sich primär für Einzelstützen, kann aber bei Berücksichtigung einer realistischen Krümmungsannahme auch für Stützen eines Gesamttragwerks angewendet werden | + | Das Modellstützenverfahren eignet sich primär für Einzelstützen, kann aber bei Berücksichtigung einer realistischen Krümmungsannahme auch für Stützen eines Gesamttragwerks angewendet werden <ref>DIN EN 1992: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken</ref>.<br /> |
Die Bemessung erfolgt nach Ermittlung der Gesamtausmitte entweder mit den Interaktionsdiagrammen für [[Druckglieder - Bemessung#Symmetrisch bewehrte Bauteile durch einachsige Biegung und Längskraft beansprucht|symmetrisch bewehrte Querschnitte]] oder direkt mit Interaktionsdiagrammen speziell für das Modellstützenverfahren. | Die Bemessung erfolgt nach Ermittlung der Gesamtausmitte entweder mit den Interaktionsdiagrammen für [[Druckglieder - Bemessung#Symmetrisch bewehrte Bauteile durch einachsige Biegung und Längskraft beansprucht|symmetrisch bewehrte Querschnitte]] oder direkt mit Interaktionsdiagrammen speziell für das Modellstützenverfahren. | ||
Version vom 31. Juli 2017, 08:29 Uhr
| Hauptseite • Stahlbetonbau • Grundlagen/Begriffe • Hinweise für Leser • Hinweise für Autoren |
Allgemeines
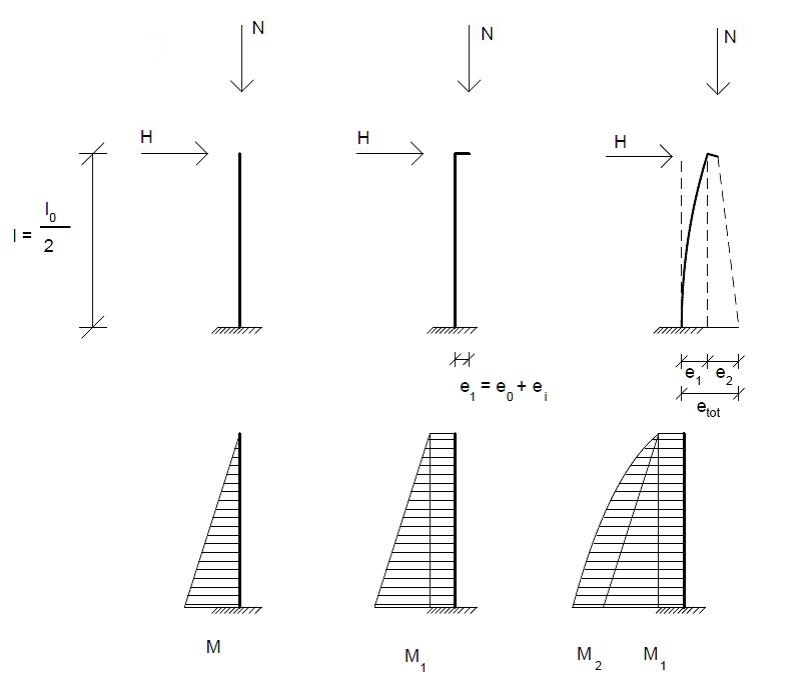
Das Verfahren mit Nennkrümmung beschreibt die näherungsweise Bestimmung der Schnittgrößen nach Theorie II. Ordnung. Es wird vereinfachend gegenüber genaueren Verfahren vorwiegend bei rechteckigen oder kreisförmigen Stahlbetonstützen angewendet, kann aber auch andere Querschnittsformen bemessen, solange die Bewehrung annähernd symmetrisch angeordnet ist [1]. Die Modellstütze ist hierbei eine Kragstütze, deren Länge die halbe Knicklänge der ursprünglich zu bemessenen Stütze beträgt und am Stützenkopf frei verschieblich ist. Die Kopfverschiebung der Modellstütze wird je nach zu erwartendem Krümmungsverlauf abgeschätzt und als zusätzliche Ausmitte in die Schnittgrößenberechnung aufgenommen.
Bedingungen
Bedingungen für die Anwendung des Verfahrens sind ein konstanter Querschnitt über die gesamte Länge und eine planmäßige Mindestausmitte von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}>0,1\cdot h}
, wobei h die Querschnittshöhe in jeweilige Richtung ist. Bei kleineren planmäßigen Ausmitten ist es nach wie vor legitim, liefert aber wegen wachsender zu sicherer Betrachtung unwirtschaftliche Ergebnisse. Nach [2] ist außerdem eine einfach gekrümmte Verformungsfigur und eine Knicklänge von maximal dem 15-fachen der jeweiligen Querschnittsabmessung Voraussetzung für das Nachweisverfahren.
Das Modellstützenverfahren eignet sich primär für Einzelstützen, kann aber bei Berücksichtigung einer realistischen Krümmungsannahme auch für Stützen eines Gesamttragwerks angewendet werden [3].
Die Bemessung erfolgt nach Ermittlung der Gesamtausmitte entweder mit den Interaktionsdiagrammen für symmetrisch bewehrte Querschnitte oder direkt mit Interaktionsdiagrammen speziell für das Modellstützenverfahren.
Erfordernis
Nach Eurocode 2 sind Auswirkungen nach Theorie II. Ordnung zu berücksichtigen, wenn sie gegenüber denen der Theorie I. Ordnung 10% größer sind. Für Einzeldruckglieder ist diese Bedingung für eine leichtere Handhabung in Form eines Grenzwertes der Schlankheit beschrieben. Hierbei gilt unter Berücksichtigung des nationalen Anhangs eine Grenzschlankheit von
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{\lim }}=25~}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left| n \right|\ge 0,41}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{\lim }}=\frac{16}{\sqrt{n}}}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left| n \right|<0,41}
mit
(Druckkraft positiv)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed}}}
- dem Bemessungswert der Normalkraft
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{c}}}
- der Betonquerschnittsfläche
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{cd}}}
- dem Bemessungswert der Betondruckkraft.
Der zweite Grenzwert erlaubt eine höhere Schlankheit als 25. Dabei wird berücksichtigt, dass bei geringerer Normalkraftbeanspruchung die Momente nach Theorie II. Ordnung entsprechend kleiner werden und demnach vernachlässigbar sind.
Schnittgrößenermittlung
Das zusätzliche Moment am Stützenfuß beträgt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2}}={{N}_{Ed}}\cdot {{e}_{tot}}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2}}}
- dem Moment nach Theorie II. Ordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}}
- der Gesamtausmitte des Stützenkopfs (mit Index total)
Die Gesamtausmitte am Stützenfuß beträgt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}={{e}_{0}}+{{e}_{i}}+{{e}_{2}}~}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}}
- der planmäßigen Ausmitte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}}
- der ungewollten Ausmitte (mit Index für imperfection)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}}
- der Ausmitte nach Theorie II. Ordnung.
Ein zusätzliches Moment und eine daraus resultierende Verformung ergibt demnach die Ausmitte als Hebelarm multipliziert mit der Längsdruckkraft.
Die planmäßige Ausmitte ergibt sich aus:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}=\frac{{{M}_{Ed}}}{{{N}_{Ed}}}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{Ed}}}
- dem Bemessungswert des Moments
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed}}}
- dem Bemessungswert der Normalkraft.
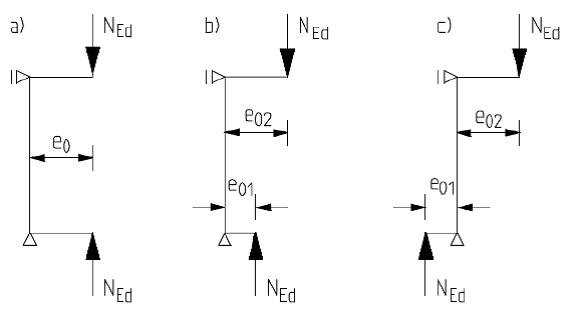
Bei unverschieblichen Stützen mit linearem Momentenverlauf entspricht die planmäßige Ausmitte bei unterschiedlichem Moment an den Stützenenden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}=\max \left\{ 0,6\cdot {{e}_{02}}+0,4\cdot {{e}_{01}}\ ;\ 0,4\cdot {{e}_{02}} \right\}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left| {{e}_{01}} \right|\le \left| {{e}_{02}} \right|}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0i}}}
- der Lastausmitte am jeweiligen Stützenende.
Die Ausmitten sind mit jeweiligen Vorzeichen einzusetzen. Hierbei wird die Ausmitte im mittleren Drittel der Stütze maßgebend.
Die ungewollte Ausmitte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}~}
(oder auch Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{a}}~}
) berücksichtigt nicht vermeidbare und kalkulierbare Einflüsse wie etwa ungerade Stabachsen, unsymmetrisch verlegte Bewehrung oder ungewollt exzentrische Lasteinleitungen.
Sie wird pauschal zur Gesamtausmitte hinzuaddiert, wenn es zum Nachweis nach Theorie II. Ordnung kommt. Ansonsten ist sie vernachlässigbar. Bei der Summierung werden stets alle Ausmitten ungünstig in dieselbe Richtung angenommen, also mit gleichem Vorzeichen. Es gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}={{\Theta }_{i}}\cdot \frac{{{l}_{0}}}{2}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\Theta }_{i}}}
- dem Grundwert
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\Theta }_{i}}=\frac{1}{200\cdot {{\alpha }_{h}}}}
im Bogenmaß
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{h}}}
- demAbminderungsbeiwert für die Höhe (mit Index für height), Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0\le {{\alpha }_{h}}=\frac{2}{{{l}^{0,5}}}\le 1}
l - der tatsächliche Länge der Stütze in [m]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}}
- der Knicklänge der Stütze
Die Ausmitte nach erfolgter Kopfverschiebung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}}
ergibt sich zu
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}=\frac{1}{r}\cdot l_{0}^{2}\cdot {{K}_{1}}\cdot \frac{1}{c}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}}
-der Krümmung
r - dem Krümmungsradius
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0}}}
- der Knicklänge
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{1}}}
- einem Faktor, um Übergang der Schlankheitsgrenzwerte zu berücksichtigen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{1}}=\frac{\lambda }{10}-2,5}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 25\le \lambda \le 35}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{1}}=1~}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda >35~}
c - einem Beiwert zum Krümmungsverlauf
Der Krümmungsverlauf wird in 3 Grenzfällen beschrieben, wobei die Kopfverschiebung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}}
sich aus dem Integral des Produktes aus virtuellem Moment und Krümmung an jeweiliger Stelle x ergibt. Je Krümmungsverlauf kommt es zu Beiwerten von
- 8 bei konstantem Momentenverlauf, also auch konstanter Krümmung
- 10 bei parabelförmigem Krümmungsverlauf
- 12 bei dreiecksförmigem Krümmungsverlauf
- 16 bei hyperbolischem Krümmungsverlauf.
Hierbei wird c = 10 üblicherweise als Mittelwert der ersten drei genannten Krümmungsverläufe gewählt. Im Gegensatz zum Eurocode 2 sieht die Fachliteratur im Allgemeinen keine Wahl des Beiwertes vor und gibt c = 10 als Konstante der Formel vor.
Die Krümmung ermittelt sich wie folgt:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}={{K}_{r}}\cdot {{K}_{\phi }}\cdot \frac{1}{{{r}_{0}}}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}}
- dem Beiwert zur Berücksichtigung der Krümmungsabnahme bei steigendem Längsdruck (mit Index für radius)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{\varphi }}}
- einem kriechberücksichtigender Beiwert
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{{{r}_{0}}}=\frac{{{\varepsilon }_{yd}}}{0,45\cdot d}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{yd}}=\frac{{{f}_{yd}}}{{{E}_{s}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{yd}}}
- dem Bemessungswert der Stahlstreckgrenze (mit Index für Stahl und design)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{E}_{s}}}
- dem Elastizitätsmodel für Stahl (mit Index für steel)
d - der statische Nutzhöhe bei gegenüberliegender Bewehrungsanordnung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d=\frac{h}{2}+{{i}_{s}}}
- bei allseitig verteilter Bewehrung
h - der Querschnittsabmessung in jeweilige Richtung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{i}_{s}}}
- dem Trägheitsradius der Bewehrung (mit Index für steel).
Der Beiwert Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}}
ist vorerst auf Grundlage folgender Gleichung abzuschätzen, da die hierin enthaltene Stahlquerschnittsfläche zu diesem Zeitpunkt des Nachweises noch nicht bekannt ist. Es empfiehlt sich eine erste Annahme zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}=1}
und einer nachfolgenden Iteration nach erstem Bemessungsdurchgang und Errechnen einer Bewehrung.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}=\frac{{{n}_{u}}-n}{{{n}_{u}}-{{n}_{bal}}}\le 1}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{n}_{bal}}}
- n bei maximaler Biegetragfähigkeit, es darf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{n}_{bal}}}
= 0,4 angenommen werden
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s}}}
- der Bewehrungsfläche.
Die Auswirkungen durch Kriechen sind bei der Berechnung nach Theorie II. Ordnung zu berücksichtigen. Sie dürfen allerdings vernachlässigt werden, wenn alle drei folgenden Bedingungen eingehalten sind:
- die Endkriechzahl Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi \left( \infty ,{{t}_{0}} \right)\le 2}
- die Schlankheit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda \le 75}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{M}_{0,Ed}}}{{{N}_{Ed}}}\ge h}
(mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{0,Ed}}}
dem Moment nach Theorie I. Ordnung).
Außerdem können sie nach [4] vernachlässigt werden, wenn sie Teil eines unverschieblichen Systems sind und an den Stützenenden jeweils monolithisch angeschlossen sind.
Bei zu vernachlässigender Kriecheinwirkung kann Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{\varphi }}=1}
gesetzt werden, andernfalls gilt
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{\varphi }}=1+\beta \cdot {{\phi }_{ef}}\ge 1}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =0,35+\frac{{{f}_{ck}}}{200}-\frac{\lambda }{150}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{ck}}}
- der charakteristische Betondruckfestigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varphi }_{ef}}=\varphi \left( \infty ,{{t}_{0}} \right)\cdot \frac{{{M}_{0,Eqp}}}{{{M}_{0,Ed}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi \left( \infty ,{{t}_{0}} \right)}
- der Endkriechzahl, zu bestimmen nach EC2 Abs. 3.1.4
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{0,Eqp}}}
- Moment nach Theorie I. Ordnung im Grenzzustand der Gebrauchstaug-lichkeit (mit Indizes Einwirkung, quasi, permanent).
Bemessung
Nach Berechnung der Schnittgrößen nach Theorie II. Ordnung können die Interaktionsdiagramme für symmetrisch bewehrte und unter Normalkraft und Moment beanspruchte Querschnitte angewendet werden.
Alternativ dazu gibt es etwa in [5] oder [6] Interaktionsdiagramme für das Verfahren mit Nennkrümmung. Hierbei sind neben den Eingangswerten der oben genannten Interaktionsdiagramme der Quotient aus Knicklänge und Querschnittsabmessung in jeweilige Richtung und die Schlankheit erforderlich. Eine Interpolation ist möglich, allerdings reicht üblicherweise auch die Wahl der nächsthöheren Schlankheit für annehmbare Ergebnisse.
Grenzen
Das Modellstützenverfahren darf bei zweiachsiger Ausmitte getrennt für beide Richtungen angewendet werden, wenn folgende Bedingungen erfüllt sind
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}\frac{{{\lambda }_{y}}}{{{\lambda }_{z}}}\le 2\\\frac{{{\lambda }_{z}}}{{{\lambda }_{y}}}\le 2\end{array}}
und
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{e}_{y}}/{{h}_{eq}}}{{{e}_{z}}/{{b}_{eq}}}\le 0,2}
oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{e}_{z}}/{{b}_{eq}}}{{{e}_{y}}/{{h}_{eq}}}\le 0,2}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{b}_{eq}}={{i}_{y}}\cdot \sqrt{12}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{h}_{eq}}={{i}_{z}}\cdot \sqrt{12}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{i}_{i}}}
- dem Trägheitsradius bezogen auf jeweilige Achse.
Bei einer gehaltenen Richtung ist diese Betrachtung natürlich hinfällig.
Als zusätzliche Bedingung gilt bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0,z}}>0,2h}
(z hierbei die stärkere Achse), dass der getrennt ablaufende Nachweis der schwächeren Achse y mit einer reduzierten Druckzonenbreite Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{h}_{red}}}
geführt wird:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{h}_{red}}=\frac{0,5\cdot h+{{h}^{2}}}{12\cdot e}\le h}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e={{e}_{0,z}}+{{e}_{i,z}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0,z}}}
- der planmäßigen Ausmitte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i,z}}}
- der ungewollten Ausmitte, beide Werte im Betrag eingesetzt.
Quellen
- ↑ Lohmeyer, G., Baar S., Ebeling, G.: Stahlbetonbau, Bemessung – Konstruktion – Ausführung, Hannover 2012
- ↑ Baumgart, R.: Skript Massivbau, Darmstadt 2013
- ↑ DIN EN 1992: Bemessung und Konstruktion von Stahlbeton- und Spannbetontragwerken
- ↑ Lohmeyer, G., Baar S., Ebeling, G.: Stahlbetonbau, Bemessung – Konstruktion – Ausführung, Hannover 2012
- ↑ Schneider, K.-J.: Bautabellen für Ingenieure, Siegen 2010
- ↑ Holschemacher, K., Müller, T., Lobisch, F.: Bemessungshilfsmittel für Betonbauteile nach Eurocode 2, Leipzig 2012
Seiteninfo
|