Lasteinzugsfläche (Bsp.)
Beispiele
In den folgenden Beíspielen wird die Lasteinzugsfläche eines deckengleichen Unterzuges berechnet.
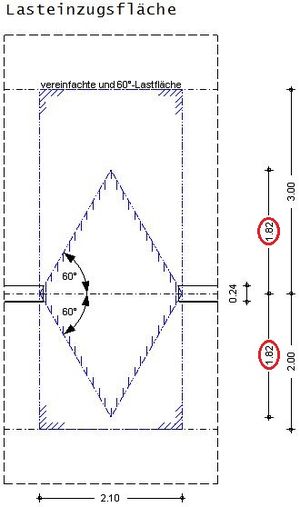
Bsp. 1
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{E}=\cfrac{l_\mathrm{eff}}{2}*tan(60)=\cfrac{2,1m}{2}*tan(60)=\underline{\underline{1,82\,\mathrm{m}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eo}=\cfrac{l_\mathrm{p,o}}{2}=\cfrac{6,0m}{2}=\underline{\underline{3,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eu}=\cfrac{l_\mathrm{p,u}}{2}=\cfrac{4,0m}{2}=\underline{\underline{2,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}
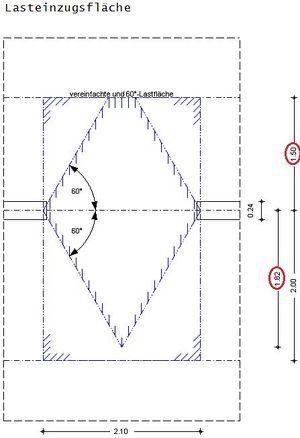
Bsp. 2
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b_\mathrm{E}=\cfrac{l_\mathrm{eff}}{2}*tan(60)=\cfrac{2,1m}{2}*tan(60)=\underline{\underline{1,82\,\mathrm{m}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eo}=\cfrac{l_\mathrm{p,o}}{2}=\cfrac{3,0m}{2}=\underline{\underline{1,5\,\mathrm{m}}}<1,82m~(l_\mathrm{Eo}~ist~massgebend)}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_\mathrm{Eu}=\cfrac{l_\mathrm{p,u}}{2}=\cfrac{4,0m}{2}=\underline{\underline{2,0\,\mathrm{m}}}>1,82m~(b_\mathrm{E}~ist~massgebend)}
Quellen
Sonstiges
- Modul-Version: 2015.0240
- Autor: T. Lange
- Veröffentlicht am: 14.04.2015
- Status: in Bearbeitung