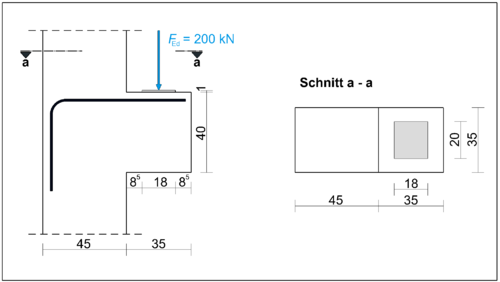
Verankerung an Konsolen (Bsp.)

Berechnungsbeispiel zur Verankerung an Konsolen

Kontext

In diesem Berechnungsbeispiel ist die Verankerungslänge der Zugbewehrung an einer Konsole nachzuweisen. Allgemeine Regeln zur Verankerungslänge und spezielle Hinweise zu Konsolen finden sich hier

Aufgabenstellung

Für die gegebene Konsole ist die Verankerung der Zugbewehrung unter der Lastplatte nachzuweisen.

Gegeben sind folgende Daten:

• Beton C35/45
• Betonstahlstahl B500B
• Gewählte Zugbewehrung: 2 Schlaufen Ø 12
• $A_{s,erf}=3,8cm^{2}$

Lösung

Verbundfestigkeit

Bewehrung oben → mäßiger Verbund

→ C35/45 → $f_{bd}=0,7\cdot 3,37N/mm^{2}=2,36N/mm^{2}=0,236kN/cm^{2}$

Stahlspannung

2 Schlaufen Ø 12 → $A_{s,vorh}=4,52cm^{2}$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\sigma}_{sd} = f_{yd} \cdot \frac{A_{s,erf}}{A_{s,vorh}} = 43,5 kN/cm^2 \cdot \frac{3,8 cm^2}{4,52 cm^2} = 36,57 kN/cm^2}

Grundwert der Verankerungslänge

$l_{b,rqd}={\frac {\emptyset _{s}}{4}}\cdot {\frac {{\sigma }_{sd}}{f_{bd}}}={\frac {1,2cm}{4}}\cdot {\frac {36,57kN/cm^{2}}{0,236kN/cm^{2}}}=46,5cm$

Ersatzverankerungslänge

$l_{b,eq}={\alpha }_{1}\cdot {\alpha }_{4}\cdot {\alpha }_{5}\cdot l_{b,rqd}$

Formgebung: Schlaufe → ${\alpha }_{1}=0,7$

Angeschweißte Querstäbe: Keine → ${\alpha }_{4}=1,0$

Querdruck: Aus aufgelagertem Bauteil → Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\alpha}_5 = 2/3}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,eq} = 0,7 \cdot 1,0 \cdot 2/3 \cdot 46,5 cm = 21,7 cm}

Mindestverankerungslänge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot {\alpha}_1 \cdot {\alpha}_4 \cdot {\alpha}_5 \cdot \left( \frac{\O_s}{4} \cdot \frac{f_{yd}}{f_{bd}} \right) \\ 10 \cdot {\alpha}_5 \cdot \O_s \end{matrix}} \right\} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 0,3 \cdot 0,7 \cdot 1,0 \cdot 2/3 \cdot \left( \frac{1,2 cm}{4} \cdot \frac{43,5 kN/cm^2}{0,236 kN/cm^2} \right) \\ 10 \cdot 2/3 \cdot 1,2 cm \end{matrix}} \right\} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_{b,min} = max\left\{ {\begin{matrix} 7,7 cm \\ 8 cm \end{matrix}} \right\} }

Nachweis der Verankerungslänge

Die Verankerungslänge beginnt an der Innenkante der Auflagerplatte.

$l_{b,vorh}=18cm+8,5cm-c_{nom}=18cm+8,5cm-3,5cm=23cm$

$l_{b,eq}=21,7cm\leq 23,0cm=l_{b,vorh}$

→ Verankerung in der geplanten Weise möglich