Durchstanzen - Korrekturfaktor β
| Stahlbetonbau • Grundlagen/Begriffe • Durchstanzen |
Korrekturfaktor β
- nach EC 2-1-1, 6.4.3.(6)
Infolge von Biegung ist die aufgebrachte Querkraft nicht mehr gleichmäßig über den Umfang verteilt, die Belastung einer Seite ist folglich erhöht. Der Lasterhöhungsfaktor β berücksichtigt diesen Umstand[1].
Zur Ermittlung des Faktors β stehen drei Verfahren zur Verfügung.
Diese werden folgend erläutert:
Konstanter Faktor für ausgesteifte Systeme mit nahezu gleichen Stützweiten
Es werden horizontal unverschiebliche, ausgesteifte Systeme mit Stützweitenunterschieden
von maximal 25 % und eine Belastung durch Gleichlast angenommen [2]. Die Stützweitenverhältnisse betragen somit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,8\leq l_1/l_2\leq 1,25}
[3].
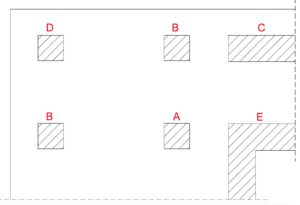
Für diesen Fall können somit folgende konstante Näherungswerte angenommen werden(siehe Bild 10):
- 1,10 Innenstützen
- 1,40 Randstützen
- 1,35 Wandenden (NA)
- 1,50 Eckstützen
- 1,20 Wandecken (NA)
- Bei Fundamenten wird ein Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta \leq 1,10} angenommen.
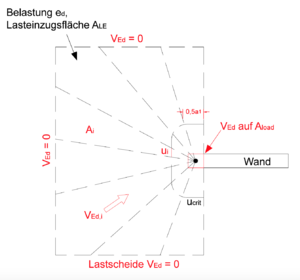
Ermittlung über Sektormodell
Im ersten Schritt sind die Querkraftnulllinien anzusätzen. Diese werden abgeschätzt
oder errechnet (linear-elastisch). Anschließend findet eine Unterteilung
der Lasteinzugsfläche in i-Lasteinleitungssektoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_i}
(siehe Bild) statt.
Hierbei sollten mindestens 3-4 Sektoren pro Quadrant betrachtet werden [4].
.
Der Lasterhöhungsfaktor ergibt sich somit wie folgt [5]:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed}=e_d \cdot A_{LE}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed,m}=\nu_Ed \cdot u_{crit}}
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta=max\{ \nu_{Ed,i}/\nu_{Ed,m}\}}
Genaueres Verfahren
nach EC 2-1-1, 6.4.3 (1;2)
Sind die oben genannten Voraussetzungen nicht erfüllt oder ist die bezogene Ausmitte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e/c}
bei Randstützen größer als 1,2 (wobei c die Stützenabmessung in Richtung der Ausmitte darstellt), ist der Lasterhöhungsfaktor mit genaueren Verfahren
zu ermitteln. Hierbei wird die Annahme einer vollplastischen Schubspannungsverteilung am kritischen Rundschnitt getroffen [6].
Die Gleichung lautet somit wie folgt:
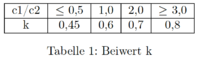
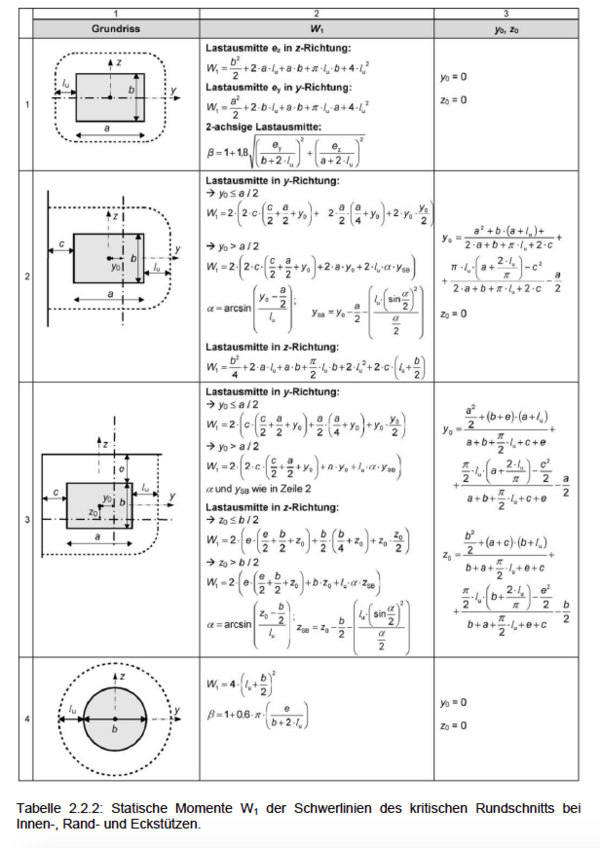
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta=1+k\cdot\frac{M_{Ed}}{V_{Ed}}\cdot\frac{u_1}{W_1}\le 1,10}
mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_1=\int_0^{u_i} |e| dl}
und somit bei einer geschlossenen Rechteckstütze mit c1 parallel und c2 senkrecht zur Lastausmitte:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_1=\frac{c_1^2}{2}+c_1c_2+4c_2d+16d^2+2\pi dc_1}
und dem Beiwert k
Bei Decken-Stützenknoten mit zweiachsiger Ausmitte gilt (NA)[5]:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle W_1=1+\sqrt{(k_y\cdot\frac{M_{Ed,y}}{V_{Ed}}\cdot\frac{u_1}{W_{1,y}})^2+(k_z\cdot\frac{M_{Ed,z}}{V_{Ed}}\cdot\frac{u_1}{W_{1,z}})^2}\ge 1,10}
Quellen
- ↑ Prof. Dipl.-Ing. Frank Prietz. Durchstanzen nach DIN EN 1992-1-1 +NA.Skript
- ↑ Dipl.-Ing. Klaus Beer. Bewehren nach DIN EN 1992-1-1(EC2). Vieweg+Teubner, S. 196-207, 3. Aufl. edition, 2012
- ↑ G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010
- ↑ K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012
- ↑ 5,0 5,1 5,2 Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012
- ↑ Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
Seiteninfo
|