Momentenausrundung (Bsp.)

Beispiel 1 Momentenausrundung über Mauerwerk

Das folgende Beispiel zeigt eine Berechnung der Momentenausrundung, wie Sie mit dem Modul S340.de geführt wird.

Aufgabe

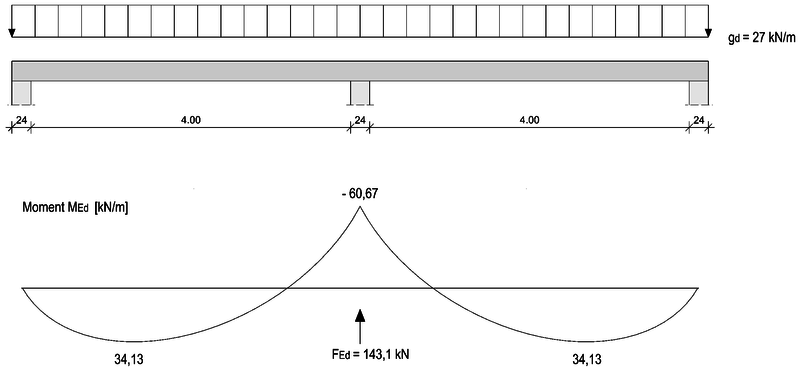
Ermittlung des Bemessungsmoment über einer frei drehbaren Lagerung, für einen Stahlbetonträger mit folgendem System:

Vorgabewerte

Die folgenden benutzten Größen sind:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{y}~....~\mathrm{Flaechentraegheitsmoment}~~~~~~~~\left([I_\mathrm{y}]=\mathrm{m}^{4}\right) }
$E~....~\mathrm {Elastizitaetsmodul} ~~~~~~~~\left([E]=\mathrm {N} \mathrm {m} ^{-2}\right)$
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l~....~\mathrm{Laenge}~~~~~~~~\left([l]=\mathrm{m}\right)}

Aus Nachlagewerk entnommene Werte seien:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{y}=18260\,\mathrm{cm}^{4}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=210000\,\mathrm{N}\mathrm{mm}^{-2}}

mit der Vorgabe einer selbst definierten Länge:
$l=5{,}00\,\mathrm {m}$

Berechnung

Durchbiegung unter einer Einzellast in Feldmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\cfrac{F\cdot l^{3}}{48\cdot E\cdot I_\mathrm{y}}}

Federsteifigkeit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\cfrac{F}{w} =\cfrac{\cancel{F}\cdot 48\cdot E\cdot I_\mathrm{y}}{\cancel{F}\cdot l^{3}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\cfrac{48\cdot 210000\,\mathrm{N}\mathrm{mm}^{-2}\cdot 18260\,\mathrm{cm}^{4}} {\left(5{,}00\,\mathrm{m}\right)^{3}} =\cfrac{48\cdot 210000\cdot 18260} {5{,}00^{3}}~\cdot ~ \cfrac{\mathrm{N}\mathrm{mm}^{-2}\cdot\mathrm{cm}^{4}} {\mathrm{m}^{3}} =Zahlenwert \cdot \cfrac{10^{-6}\,\mathrm{N}\mathrm{m}^{-2}\cdot 10^{-8}\,\mathrm{m}^{4}} {\mathrm{m}^{3}} =...=\underline{\underline{147249\,\mathrm{kN}\mathrm{m}^{-1}}} }

Sonstiges

• Modul-Version: 2014.011
• Autor: R. Wengatz
• Veröffentlicht am: 24.02.2015
• Status: in Bearbeitung