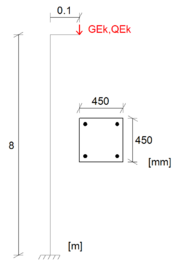
Stahlbeton-Kragstütze im Brandfall (Bsp.)

Ein Beispiel für die Berechnung einer Stahlbeton-Kragstütze nach dem vereinfachten Verfahren des nationalen Anhang AA des EC 2-1-2.

Aufgabenstellung

Gegeben

• Kragstütze, vierseitig beflammt, in einer Versammlungsstätte (Kategorie C)
• h/b = 450/450mm
• L = 8m
• Lastausmitte e₁ = 0,1m
• Beton C40/50, f_cd = 22,67N/mm²
• Stahl B500B, f_yd = 435N/mm²
• Bewehrungsverhältnis ρ = 0,02 = 2%
• Achsabstand a = 50mm
• G_Ek = 50kN; Q_Ek = 75kN

Gefordert

Für die Stahlbeton-Kragstütze soll eine Feuerwiderstandsdauer von 90 Minuten nachgewiesen werden.

Nachweis

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle |{{\nu}_{E,fi,d}}| \leq |{{\nu}_{R,fi,d,90}}|}

νE,fi,d	Längskrafteinwirkung
νR,fi,d,90	Normalkrafttragfähigkeit

Längskrafteinwirkung (ν_E,fi,d)

${{N}_{E,fi,d}}={{N}_{Gk}}+{{\psi }_{2,1}}\cdot {{N}_{Qk}}=50kN+0,6\cdot 75kN=92kN$

${{\nu }_{E,fi,d}}={\frac {{N}_{E,fi,d}}{{A}_{c}\cdot {f}_{cd}}}$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{c}} = \frac{{{(45cm)}^{2}}}{{{100%}}}\cdot98% = 1984,5cm^2}

${{\nu }_{E,fi,d}}={\frac {92\cdot 10^{3}kN}{(22,67N/mm^{2}\cdot 198450mm^{2})}}=0,020$

Normalkrafttragfähigkeit (ν_R,fi,d,90)

Überprüfung der Randbedingungen

• Normalbeton

	zwischen C20/25 und C50/60
	C40/50; Randbedingung erfüllt
	Abweichung von kc erforderlich, da C40/50 ≈ C30/37

• Bewehrungslage

einlagige Bewehrung; Randbedingung erfüllt

• Querschnittsabmessungen

450mm; Randbedingung erfüllt

• geometrischer Bewehrungsgrad (ρ)

	1% ≤ 2% ≤ 8%; Randbedingung erfüllt
	kρ=1,0, da ρ = 2%. Es ist keine Abweichung erforderlich.

• bezogener Achsabstand (a/h)

	Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,05 \le \frac{{{50}}}{{{450}}} = 0,11 \le 0,15} ; Randbedingung erfüllt
	ka = 0,11 ≈ 0,10. Abweichung von Ka erforderlich.

• bezogene Knicklänge (l_0,fi/h)

$10\leq 2\cdot {\frac {8m}{0,45m}}=35,6\leq 50$; Randbedingung erfüllt

• bezogene Lastausmitte (e₁/h)

${\frac {0,10m}{0,45m}}=0,22\leq 1,5$; Randbedingung erfüllt

• Brandbeanspruchung

4-seitige Brandbeanspruchung, keine Abweichung kfi erforderlich.

Standarddiagramm (für 450mm)

Standarddiagramm für eine 450mm Stahlbeton-Kragstütze

Standarddiagramm mit den Eingangswerten l0,fi = 35,6 und e1/h = 0,22

• mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0,fi}} = 35,6} und ${\frac {{e}_{1}}{h}}=0,22$
• Mit dem Standarddiagramm ergibt sich X_R,90 mit:

${{X}_{R,90}}=-0,095$

Gleichung zur Berechnung der Normaltragkraft ν_R,fi,d,90

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\nu}_{R,fi,d,90}} = {{k}_{fi}}\cdot{{k}_{a}}\cdot{{k}_{C}}\cdot{{k}_{\rho}}\cdot{{X}_{R90}}}

kfi = 1,0	da 4-seitig beansprucht
kρ = 1,0	da ρ = 2%
XR90 = -0,095	aus dem Standarddiagramm

Beiwert k_a

${{k}_{a}}={\frac {(h\prime -1)}{0,05}}\cdot ({\frac {a}{h}})-2\cdot h\prime +3$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h\prime = max\{0,65\cdot(\frac{{{5-h}}}{{{150}}})-{{k}_{1}};1\}}

${{k}_{1}}=max\{0,65\cdot (1-({\frac {{e}_{1}}{h}}))\cdot (3-{\frac {h}{150}});0\}$

${{k}_{1}}=0,65\cdot (1-({\frac {100}{450}}))\cdot (3-{\frac {450}{150}})=0$

$h\prime =0,65\cdot (5-{\frac {450}{150}})-0=1,3$

${{k}_{a}}={\frac {1,3-1}{0,05}}\cdot ({\frac {50}{450}})-2\cdot 1,3+3=1,067$

Beiwert k_c

${{k}_{c}}=({\frac {{k}_{1}-1}{20}})\cdot {{f}_{ck}}-1,5\cdot {{k}_{1}}+2,5$

${{k}_{1}}=max\{1,1-0,1\cdot ({\frac {{e}_{1}}{h}});1\}$

${{k}_{1}}=1,1-0,1\cdot ({\frac {100}{450}})=1,078$

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{k}_{c}} = (\frac{{{1,078-1}}}{{{20}}})\cdot40-1,5\cdot1,078+2,5 = 1,039}

Ergebnis der Normalkrafttragfähigkeit

${{\nu }_{R,fi,d,90}}=1\cdot 1,067\cdot 1,039\cdot 1\cdot (-0,095)=-0,105$