Brandschutznachweis Stahlbetonstütze (Bsp.)

Methode A (Tafel)

Gegeben:

Stahlbetonpendelstütze:
- unverschieblich
- beidseitig gelenkig gelagert
- Nutzung als Verkaufsraum
- allseitig beflammt
- gefordert: R60

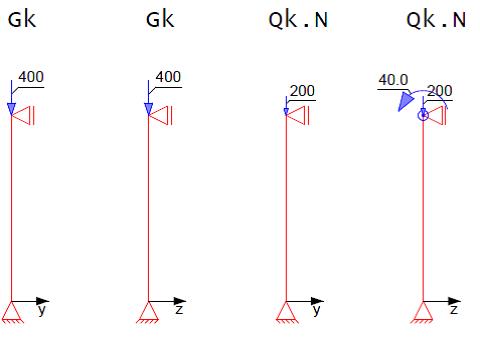
Einwirkungen

Querschnitts- und Systemabmessungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}b/h=30/30\\l=3m\\\frac{{{d}_{1}}}{h}=\frac{0,054}{0,3}=0,18\approx 0,2\end{array}}

auf sichere Seite gerundet

Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{N}_{Ed}}=1,35\cdot 400+1,5\cdot 200=840kN\\{{M}_{Ed}}=66,3kNm\end{array}}

ohne Rechnung, einschließlich Theorie II. Ordnung

Kaltbemessung

Bezogene Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-840}{30\cdot 30\cdot 0,85\cdot \frac{2,0}{1,5}}=-0,82\\{{\mu }_{Ed}}=\frac{{{M}_{Ed}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{6630}{30\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,0}{1,5}}=0,22\end{array}}

Interaktionsdiagramm

Ermittlung des mechanischen Bewehrungsgrades, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{tot}}=0,56~}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s}}={{\omega }_{tot}}\cdot \frac{b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}=0,56\cdot \frac{0,3\cdot 0,3}{\frac{50}{1,15}/\left( 0,85\cdot \frac{2}{1,5} \right)}=13,09cm{}^\text{2}}

gewählt: 2x 6ø12, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s}}=13,57cm{}^\text{2}~}

Heißbemessung

Bedingungen

- Bewehrungsgrad ${\frac {13,57}{30\cdot 30}}=0,015\leq 0,04$
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{l}_{0,fi}}=3\le 3}

Bemessung nach Tafel legitimiert.

Außergewöhnliche Einwirkungskombination während des Brandfalls

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN}

Ermittlung des Reduktionsfaktors

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62}

Bezogene Schnittgrößen

(vereinfacht mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 0,62\cdot {{\nu }_{Ed}}} oder genauer mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc}}=1,0~} ):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed,fi,t}}=\frac{{{N}_{Ed,fi}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-520}{30\cdot 30\cdot \frac{2,0}{1,5}}=-0,43\\{{\mu }_{Ed,fi,t}}=\frac{{{M}_{Ed,fi}}}{b\cdot {{h}^{2}}\cdot {{f}_{cd}}}=\frac{0,62\cdot 6630}{30\cdot 30{}^\text{2}\cdot \frac{2,0}{1,5}}=0,11\end{array}}

Mechanischer Bewehrungsgrad

bei Berücksichtigung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\alpha }_{cc}}=1,0~} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/\frac{2,0}{1,5} \right)}{30\cdot 30}=0,49}

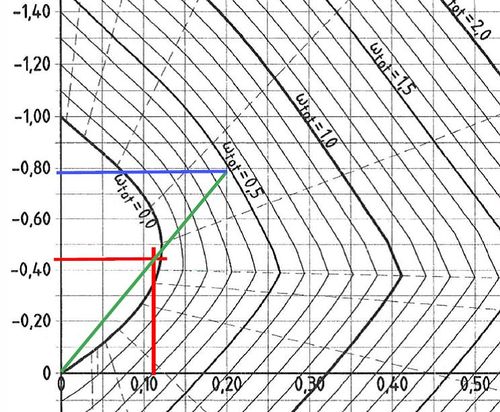
Ermittlung der zulässigen bezogenen Normalkraft mithilfe des Interaktionsdiagramms

Vom Diagrammnullpunkt über den Schnittpunkt der bezogenen heißbemessenen Schnittgrößen wird der mechanische Bewehrungsgrad angezielt und damit ${{\nu }_{Ed,fi,t,zul}}=-0,79~$ abgelesen.
Der Bemessungswiderstand der Normalkraft ergibt sich durch Wiedereinführen der Abmessungen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Rd}}={{\nu }_{Ed,fi,t,zul}}\cdot b\cdot h\cdot {{f}_{cd}}=-0,79\cdot 30\cdot 30\cdot \frac{2}{1,5}=-948kN}

Das Verhältnis aus Einwirkung und Widerstand ergibt den Ausnutzungsgrad

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\mu }_{fi}}=\frac{{{N}_{Ed,fi,t}}}{{{N}_{Rd}}}=\frac{-520}{-948}=0,55}

Durch Interpolation ergeben sich in der Tafel des Eurocode 2 für Methode A mit geforderter Brandwiderstandsdauer von 60 Minuten die folgenden Mindestabmessungen und Achsabstände:

212,5mm/38,5mm oder 312,5mm/33,25mm

Stütze mit 300mm/54mm eingehalten, Nachweis erfüllt.

Anmerkungen:
In der Vergleichsrechnung mit dem Modul S402.de wird die „kalte“ Einwirkungskombination mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{G,\inf }}} , jedoch auch mit ${{\gamma }_{Q,\sup }}$ berechnet. Weiterhin ist der Bemessungswert der „heißen“ Einwirkungskombination nicht nachzuvollziehen. Als Konsequenz ergibt sich ein höherer Ausnutzungsfaktor und eine entsprechend höhere Forderung zum Einhalten der Forderung R60.
Eine Nachweisführung mit Methode B kann in diesem Fall nicht erfolgen, weil die Stütze eine Schlankheit von 30 als Bedingung übersteigt.

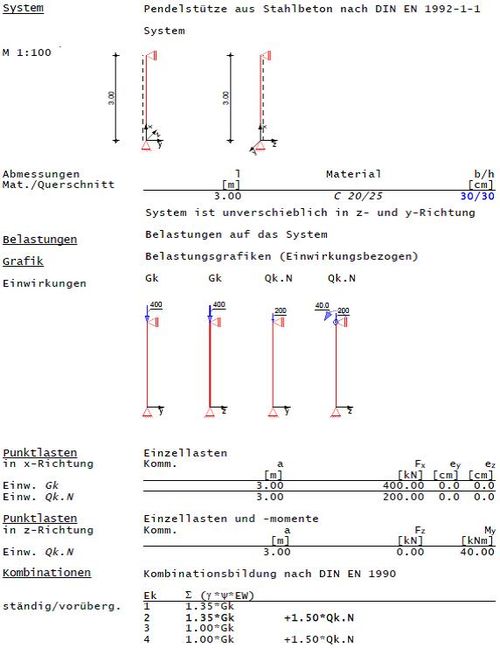
mb-Vergleichsrechnung

Methode A (Gleichung)

Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A).
Die Vorgehensweise zu Ermittlung des Ausnutzungsgrades ist dieselbe.

Mechanischer Bewehrungsgrad

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\omega }_{vorh}}=\frac{{{A}_{s,vorh}}\cdot ({{f}_{yd}}/{{f}_{cd}})}{b\cdot h}=\frac{13,57\cdot \left( \frac{50}{1,15}/0,85\cdot \frac{2,0}{1,5} \right)}{30\cdot 30}=0,58}

Ermittlung der Summanden

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{R}_{\eta ,fi}}=83\cdot \left( 1-{{\mu }_{fi}}\cdot \frac{1+\omega }{(0,85/{{\alpha }_{cc}})+\omega } \right)=83\cdot \left( 1-0,55\cdot \frac{1+0,58}{(0,85/1)+0,58} \right)=32,56\\{{R}_{a}}=1,6\cdot (a-30)=1,6\cdot \left( 54-30 \right)=38,4\\{{R}_{l}}=9,6\cdot (5-{{l}_{0,fi}})=9,6\cdot (5-3)=19,2\\{{R}_{b}}=0,09\cdot b'=0,09\cdot \frac{2\cdot {{A}_{c}}}{b+h}=0,09\cdot \frac{2\cdot (300{}^\text{2}-1357)}{300+300}=26,59\\{{R}_{n}}=12\end{array}}

Ermittlung der Branddauer

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R=120\cdot {{\left( \frac{{{R}_{\eta ,fi}}+{{R}_{a}}+{{R}_{l}}+{{R}_{b}}+{{R}_{n}}}{120} \right)}^{1,8}}=120\cdot {{\left( \frac{32,56+38,4+19,2+26,59+12}{120} \right)}^{1,8}}=136\min }

Nachweis erfüllt.

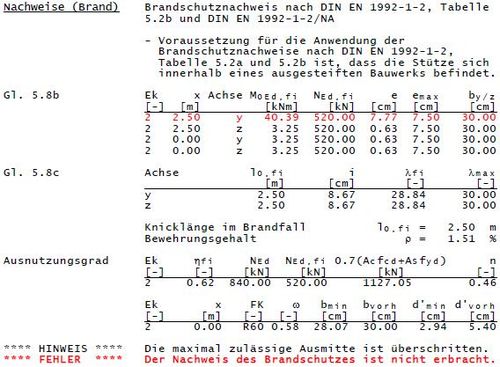
mb-Vergleichsrechnung

Methode B

Grundlage sind das System und die Einwirkungen aus Beispiel (Methode A). Die Länge wird hier mit Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle l=2,5m} vorgegeben. Das Moment nach Theorie II. Ordnung ergibt sich zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{Ed,2}}=65,25kNm~} .

Mechanischer Bewehrungsgrad

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{13,57\cdot \frac{50}{1,15}}{\left( {{30}^{2}}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}}=0,59a}

Außergewöhnliche Einwirkungskombination während des Brandfalls

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{N}_{Ed,fi}}={{N}_{G}}+{{\psi }_{2}}\cdot {{N}_{Q}}=400+0,6\cdot 200=520kN}

Ermittlung des Reduktionsfaktors

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\eta }_{fi}}=\frac{{{N}_{Ed,fi}}}{{{N}_{Ed}}}=\frac{520}{840}=0,62}

Ermittlung des Ausnutzungsgrades

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed,fi}}}{0,7\cdot \left( {{A}_{c}}\cdot {{f}_{cd}}+{{A}_{s}}\cdot {{f}_{yd}} \right)}=\frac{520}{0,7\cdot \left[ \left( 30{}^\text{2}-13,57 \right)\cdot 0,85\cdot \frac{2}{1,5}+13,57\cdot \frac{50}{1,15} \right]}=0,47}

Zulässige Knicklänge

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{fi,t}}=\frac{{{l}_{0,fi}}}{i}=\frac{{{l}_{0,fi}}}{\sqrt{\frac{I}{A}}}=\frac{250}{\sqrt{\frac{{{30}^{4}}/12}{{{30}^{2}}}}}=28,87\le 30}

Zulässige Ausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e=\frac{{{M}_{0,Ed,fi}}}{{{N}_{Ed,fi}}}=\frac{0,62\cdot 65,25}{520}=0,079m>b\cdot 0,25=0,075m}

Bedingung nicht erfüllt, ein Eingang in die Tafel ist hinfällig.

mb-Vergleichsrechnung

Quellen

Seiteninfo Status: Seite fertig, ungeprüft