Durchstanzen - Besonderheiten von Fundamenten

Aus Baustatik-Wiki
Zur Navigation springen Zur Suche springen


Besonderheiten bei der Ermittlung des Bemessungswertes der einwirkenden Querkraft

Allgemeines

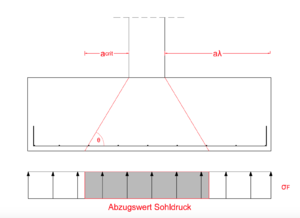
Bei Bodenplatten und Stützenfundamenten darf in der Fläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{crit}} die Einwirkung vollständig um den günstig wirkenden Sohldruck abgemindert werden.
Durch die Bodenpressung und eine geringere Schubschlankheit fällt darüber hinaus der Durchstanzkegel deutlich steiler aus als bei schlanken Deckenplatten. Aufgrund dessen ist die Lage des maßgeblichen Rundschnitts im Voraus nicht bekannt [1].
Die reduzierte Querkraftbeanspruchung ermittelt sich wie folgt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed, red}=V_{Ed}-\Delta V_{Ed}}


wobei:

VEd - gesamte aus der Stützennormalkraft resultierende Querkraft im kritischen Rundschnitt
ΔVEd - Gesamtwert der innerhalb der kritischen Fläche wirkenden Bodenpressung
VEd,red - um den Betrag der innerhalb der kritischen Fläche wirkenden Bodenpressung reduzierte Querkraft im kritischen Rundschnitt

Der im Vornherein unbekannte Abstand acrit lässt sich wie folgt ermitteln (NA):

  • gedrungene Fundamente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda \le 2,0 } : iterative Ermittlung des kritischen Rundschnitts
  • schlanke Fundamente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda >2,0} : konstanter Rundschnitt im Abstand 1,0d.


mit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda=\frac{a_{\lambda}}{d}}


und der Bedingung:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{crit}\le 2d}



Ermittlung der Sohlpressung bei ausmittig belasteten Fundamenten mit klaffenden Fugen im Rundschnittbereich

In diesem Fall Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (e = l/6)} sollte die Berechnung über einzelne Sektoren erfolgen. Der abzuziehende Wert für den Sohldruck ergibt sich somit für jeden Sektor separat [2].


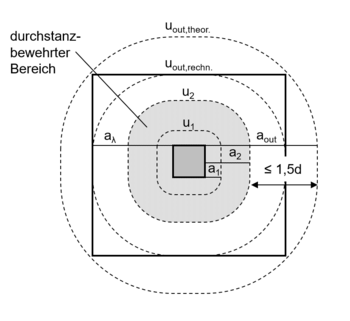
Ermittlung des Abstandes acrit

Diagramm zur grafischen Herleitung des maßgebenden Rundschnitts bei Einzelfundamenten

Wenn die Lage des kritischen Rundschnitts iterativ ermittelt werden muss, dann ist derjenige Rundschnitt maßgebend, in welchem - unter Berücksichtigung des Abzugs der Sohlpressung innerhalb der kritischen Fläche - die größte Auslastung auftritt. Das zugehörige Kriterium kann mit der nachfolgenden Bedingung angegeben werden. Im kritischen Rundschnitt erreicht dieses Kriterium ein Minimum.

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{V_{Rd,c}}{1-\frac{A_{crit}}{A_{Fund}}}= Minimum}


wobei:

VRd,c - Gesamtwert der ohne Durchstanzbewehrung aufnehmbaren Querkraft im kritischen Rundschnitt
Acrit - Flächeninhalt der durch den kritischen Rundschnitt eingeschlossenen Fläche
AFund - Fundamentfläche



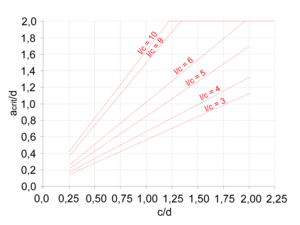
Neben der aufwändigen iterativen Methode zur Ermittlung von acrit bietet das aufgezeigte Diagramm (siehe Bild) eine alternative Bestimmungsoption. Dieses stellt die Zusammenhänge der folgenden Eingangsparameter dar [3]:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{c}{d} } und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{l}{c}}

mit
l- Fundamentlänge
c- Stützenbreite
d- statische Nutzhöhe


Zudem ist es möglich Iteration von einer Excel-Anwendung durchführen zu lassen. Dadurch spart man einiges an Zeit und kann verschiedene Fundamentmaße überprüfen, um einen möglichst wirtschaftlichen Querschnitt zu ermitteln. Es müssen lediglich die Fundamentmaße, die Materialparameter und der Längsbewehrungsgrad eingegeben werden. Dann wird eine Tabelle sowie ein Graph erstellt, an dem man den kritischen Rundschnitt ablesen kann.

Dazu einfach auf den folgenden Link drücken, um die Anwendung herunterzuladen:

→Exel-Anwendung←



Besonderheiten bei Fundamenten ohne Durchstanzbewehrung

Bei Fundamenten ohne vorherrschende Normalspannung und somit einem

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{cp} = 0} , wird der Nachweis wie folgt geführt:


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed}\le\nu_{Rd}=C_{Rd,c}\cdot k\cdot (100\cdot f_{ck})^{1/3}\cdot\frac{2d}{a_{crit}}\ge\nu_{min}\cdot\frac{2d}{a_{crit}}} (NA)



Da bei Fundamenten ein Einfluss der Schlankheit vorherrscht, wird das geforderte Zuverlässigkeitsniveau nicht erreicht, folglich muss die Gleichung angepasst werden [4]:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_{Rd,c}=0,15/\gamma_c}
Fundament ohne Durchstanzbewehrung

mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_c=1,5}
Die Einwirkung setzt sich hierbei folgendermaßen zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Ed}=\beta\cdot\frac{V_{Ed,red}}{u_{crit\cdot d}}}

mit

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta\ge 1,10 } (NA)


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta= 1,10 } (NA) für mittige Belastung
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \beta =1+k\cdot {\frac {M_{Ed}\cdot u_{crit}}{V_{Ed,red}\cdot W}}} für aussermittige Belastung


Es besteht somit eine Analogie zwischen dem Nachweis der Durchstanztragfähigkeit und der Ermittlung der Querkrafttragfähigkeit bei biegebewehrten Stahlbetonbauteilen. Da durch den rotationssymmetrischen Durchstanzkegel eine höhere Rissverzahnung vorliegt, fällt die Durchstanztragfähigkeit jedoch höher aus [5].

Besonderheiten von Fundamenten mit Durchstanzbewehrung


Bei Fundamenten ist die reduzierte einwirkende Querkraft Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle V_{Ed,red}} von den ersten zwei Bewehrungsreihen voll aufzunehmen, dabei ist der Betontraganteil nicht in Abzug zu bringen. Die erforderliche Bewehrung ist gleichmäßig auf die ersten beiden Reihen zu verteilen [6].


Die Maximaltragfähigkeit des Fundaments setzt sich folgendermaßen zusammen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rd,max}=1,4\cdot\nu_{Rd,c,u1}}


Bei Fundamenten ist u1 gegebenenfalls durch den interativ ermittelten Wert von u im Abstand acrit zu ersetzen. Hier darf bei der Ermittlung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \nu_{Rd,c}} keine Betondruckspannung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma_{cp}} durch eine Vorspannung berücksichtigt werden [6]. Wird der Maximalwert überschritten, so müssen Maßnahmen zur Steigerung des Querkraftwiderstands ergriffen werden.

Hierzu gehören [3]

  • Erhöhung der Betongüte
  • Vergrößerung der Fundamentenhöhe
  • oder Erhöhung des Bewehrungsgrades


Folgende Nachweise sind zu führen [4]:

  • für Bügelbewehrung:


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta\cdot V_{Ed,red}\le V_{Rd,s}=A_{sw, 1+2}\cdot f_{ywd,ef}}


Umgestellt zur Ermittlung der Bewehrungsmenge:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{sw, 1+2}=\frac{\beta\cdot V_{Ed,red}}{f_{ywd,ef}}}

  • für Schrägbewehrung:


Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta\cdot V_{Ed,red}\le V_{Rd,s}=1,3\cdot A_{sw, 1+2}\cdot f_{ywd,ef}\cdot \sin(\alpha)}


Weitere eventuell erforderliche Bewehrungsreihen werden mit 33 % von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A_{sw,1+2}} versehen.

einzuhaltende radialen Abstände der Durchstanzbewehrung nach EC2-1-1/NA
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle A_{sw,2+i}=0,33\cdot A_{sw,1+2}}


Hierbei darf innerhalb der betrachteten Bewehrungsreihe die Bodenpressung der Fundamentfläche in Abzug gebracht werden [2].


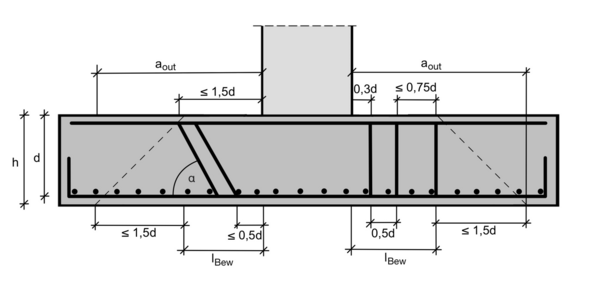
Bei der Verlegung der Bügelbewehrung sind radiale sowie tangentiale Abstände einzuhalten.

radialen Abstände:

  • 1. Reihe im Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_0=0,3d}
  • 2. Reihe im Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_0+s_1= 0,3d + 0,5d = 0,8d}
  • 3. Reihe im Abstand Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_0+s_1+s_i = 0,3d + 0,5d + 0,75d = 1,55d } → bei gedrungenen Fundamenten: Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle s_{0}+s_{1}+s_{i}=0,3d+0,5d+0,5d=1,3d}


äußerer Rundschnitt liegt außerhalb des Fundaments

tangentialen Abstände:

  • 1. innerhalb des kritischen Rundschnitts Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_t \le 1,5d}
  • 2. außerhalb des kritischen Rundschnitts Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle s_t \le 2,0d}



Wenn der äußere Rundschnitt außerhalb des Einzelfundaments liegt (siehe Bild), dann wird eine dritte Bewehrungsreihe wird nicht mehr benötigt, da bereits ein Großteil des äußeren Rundschnitts außerhalb des Fundaments liegt. Da aout außerhalb des Fundaments liegt, wird mit aλ weitergerechnet. Der günstig wirkende Sohldruck kann vollständig innerhalb der äußeren Rundschnitts angesetzt werden, wodurch die einwirkende Querkraft fast vollständig reduziert wird.





Quellen

  1. ↑ Markus Ricker. Zur Zuverlässigkeit der Bemessung gegen Durchstanzen bei Einzelfundamenten. Dissertation (Reihnisch-Westfälische Technischen Hochschule Aachen), 2009
  2. ↑ 2,0 2,1 G. Zehetmaier K. Zilch. Bemessung im konstruktiven Betonbau. Springer, S.313-361, 2. Aufl. edition, 2010
  3. ↑ 3,0 3,1 Dr.-Ing. Markus Staller/Dipl.-Ing. Christian Juli. Durchstanzen von Flachdecken und Fundamenten. Hochschule München- Einführung in den Eurocode 2 mit Praxisbeispielen und Konstruktion im Stahlbeton- und Spannbetonbau, 2012
  4. ↑ 4,0 4,1 Prof. Dr-Ing. Jens Minnert. Durchstanzen nach EC 2-1-1 und EC 2-1-1/NA. mb AEC- Fit für den Eurocode, 2012
  5. ↑ Prof. Dr.-Ing. Rudolf Baumgart. Durchstanznachweis nach EC 2. Skript Hochschule Darmstadt-University of Applied Sciences, 2012.
  6. ↑ 6,0 6,1 K. Zilch F. Fingerloos, J. Hegger. Eurocode 2 für Deutschland. Ernst + Sohn, Beuth-Verlag, S. 263-281, 1. Aufl. edition, 2012
Seiteninfo
Quality-flag-white.gif
Status: Seite in Bearbeitung
Modul-Version: 2015.0240
Abgerufen von „https://baustatik-wiki.fiw.hs-wismar.de/mediawiki/index.php?title=Durchstanzen_-_Besonderheiten_von_Fundamenten&oldid=15353“