Querkraftbemessung
| Hauptseite • Stahlbetonbau • Grundlagen/Begriffe • Hinweise für Leser • Hinweise für Autoren |
Allgemeines
Der Nachweis der ausreichenden Querkrafttragfähigkeit ist mit der Bedingung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{V}_{Ed}}\le {{V}_{Rd}}}
erfüllt.
Die aufnehmbare Querkraft kann durch die drei folgenden Werte bestimmt sein:
- VRd,c - Bemessungswert der aufnehmbaren Querkraft ohne Schubbewehrung (Index c für concrete, da die Zugstreben durch die Rissverzahnung zwischen den Betonzähnen ersetzt werden)
- VRd,s - Bemessungswert der aufnehmbaren Querkraft (begrenzt auf die Tragfähigkeit der Querkraftbewehrung) mit Schubbewehrung als Zugstrebe (Index s für steel).
- VRd,max - Bemessungswert der Querkraft, begrenzt durch die Tragfähigkeit der Betondruckstrebe. Diese Bedingung muss in allen Querschnittsbereichen erfüllt sein.
Für den Fall, dass VEd ≤ VRd,c ist rechnerisch keine Querkraftbewehrung erforderlich.
Bei Balken und Platten mit b/h ≤ 5,0 ist eine Mindestbewehrung vorzusehen.
Wenn VEd > VRd,c muss die Querkraftbewehrung bemessen werden.
Der Bemessungswert der Querkraft VEd darf den Bemessungswiderstand VRd,max keinesfalls überschreiten.
Bemessungsmodelle
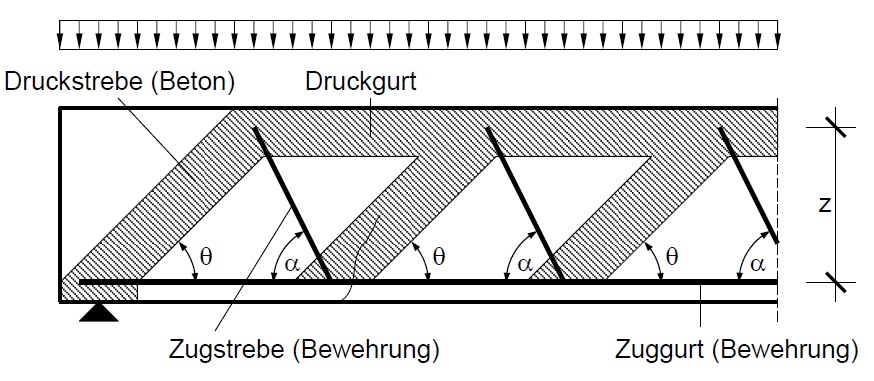
Die Bemessung erfolgt auf der Grundlage einer Fachwerkanalogie.
Dabei wird von einem Fachwerkmodell im klassischen Stahlbetonbalken ausgegangen:
- Betondruckzone als Druckgurt
- Längsbewehrung als Zuggurt
- Druckdiagonalen im Beton
- gegebenenfalls angeordnete Querkraftbewehrung als Zugstreben.
Bauteile ohne rechnerisch erforderliche Querkraftbemessung
Auch ohne Bügelbewehrung kommt es durch die Kornverzahnung in den Rissen und der Dübelwirkung der Längsbewehrung zu begrenzter Querkrafttragfähigkeit. Die Grenze ist hierbei die Betonzugfestigkeit in den Einspannungen der sich ausgebildeten Betonzähne. Zum Nachweis gehört folgende Gleichung:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{V}_{Rd,c}}=[{{C}_{Rdc}}\cdot k\cdot {{(100\cdot {{\rho }_{l}}\cdot {{f}_{ck}})}^{\frac{1}{3}}}+0,12\cdot {{\sigma }_{cp}}]\cdot {{b}_{w}}\cdot d\ge {{V}_{Rd,c,\min }}}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{C}_{Rdc}}=\frac{0,15}{{{\gamma }_{c}}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=1+\sqrt{\frac{200}{d}} \left\{ \begin{matrix} \ge 1,0 \\ \le 2,0 \\ \end{matrix} \right\}}
[mm] Beiwert zur Berücksichtigung der Bauteilhöhe (Maßstabseffekt)
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{b}_{w}}~}
- der kleinsten Querschnittsbreite innerhalb der Zugzone(mit Index w für width) [mm]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d~}
- der statischen Nutzhöhe [mm]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{f}_{ck}}~}
- der charakkteristische Betondruckspannung [N/mm²]
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\sigma }_{cp}}=\frac{{{N}_{Ed}}}{{{A}_{c}}} \le 0,2\cdot {{f}_{cd}}}
[N/mm²] einwirkende Längsspannungen, Druck hierbei positiv einzusetzen
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\rho }_{l}}=\frac{{{A}_{sl}}}{{{b}_{w}}\cdot d}\le 0,02}
geometrischer Bewehrungsgrad der Längsbewehrung
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\gamma }_{c}}=1,5~}
bei ständiger und vorübergehender Bemessungssituation
Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{\gamma }_{c}}=1,3~}
bei außergewöhnlicher Bemessungssituation
Die Gleichung ist nicht dimensionsrein.
Manche Formeln der Fachliteratur beinhalten dabei noch einen zusätzlichen Faktor, der die Querkrafttragfähigkeit bei Leichtbeton abmindert.
Die der Querkraft entgegenwirkende Verzahnung und Dübelwirkung ist in der Formel mit enthalten. Weiterhin berücksichtigt der Faktor k eine Abminderung der Tragfähigkeit bei wachsender Bauteilhöhe [vgl. [1]] und σ die gegebenenfalls auftretenden, günstig wirkenden Längsdruckkräfte.
Eine Mindestquerkrafttragfähigkeit wird bei geringeren Längsbewehrungsgraden maßgebend, da die ursprüngliche Gleichung zu sichere Ergebnisse ausgibt.
Sie formuliert sich zu
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{V}_{Rd,c,\min }}=\left[ \frac{{{\kappa }_{1}}}{{{\gamma }_{c}}}\cdot {{\left( {{k}^{3}}\cdot {{f}_{ck}} \right)}^{0,5}}+0,12\cdot {{\sigma }_{cp}} \right]\cdot {{b}_{w}}\cdot d}
mit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\kappa }_{1}}=0,0525~}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d\le 60cm}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\kappa }_{1}}=0,0375~}
für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d\ge 80cm}
(Zwischenwerte sind zu interpolieren)
Quellen
- ↑ Goris, A.: Stahlbetonbau-Praxis nach Eurocode 2, Band 1: Grundlagen, Bemessung, Beispiele, Siegen 2013
Seiteninfo
|