Auflagerbreite (S220.de)

Eingabe

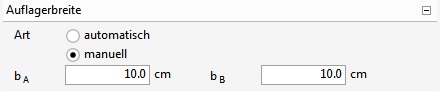
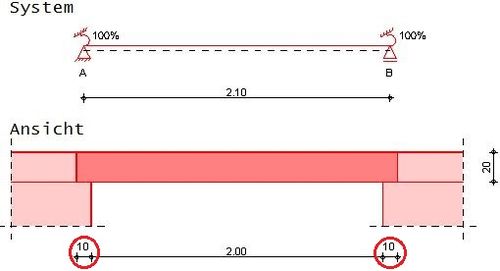
Die Auflagerbreiten "b_A" und "b_B" [cm] können automatisch vom Modull bestimmt, oder manuell eingetragen werden (0 ≤ b_A,B ≤ 999)

Berechnungsgrundlagen

Hinweis:

• Bei der automatischen Ermittlung der Auflagerbreite wird für b folgender Wert gesetzt:

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle b_{\mathrm {A,B} }=max~(10cm,~(3-{\cfrac {E}{100\%}})*l_{\mathrm {eff} }*{\cfrac {0,025}{1,05}})}

Um zu verstehen, was hinter dieser Berechnung steckt, wird die Formel im Folgenden näher betrachtet. Dabei ist zu beachten, dass die Auflagerbreite auf maximal 10cm begrenzt wird. Bei der Untersuchung fällt auf, dass die Formel aus zwei Teilen zusammengesetzt ist:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}b_\mathrm{A,B} = Auflagerart * a_\mathrm{i}\end{align}}

Wobei:

• Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Auflagerart = (3-\cfrac{E}{100%})}
• Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i} = l_\mathrm{eff} * \cfrac{0,025}{1,05}}
  
  

Auflagerart:
Das Modul berücksichtigt noch die DIN 1045-1, 7.3.1, in der die Auflagerbreite abhängig von der Einspannung ist und anderen Werten als nach EC2-1-1, 5.3.2.2 entspricht.

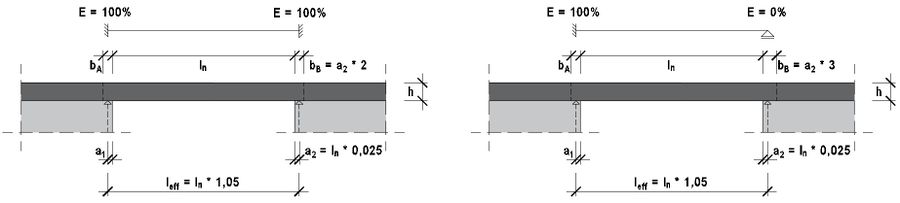
• Auflager mit voller Einspannung (E = 100%):
  
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}b_\mathrm{A,B} = a_\mathrm{i} * 2\end{align}}

• Frei drehbares Endauflager (0% ≤ E ≤ 100%):
  
  

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i} * 2 \le b \le a_\mathrm{i} * 3}

→ Aus den beiden Bedingungen ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}Auflagerart = (3-\cfrac{E}{100%})\end{align}}

a_i:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{eff} = l_\mathrm{n} * 1,05\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{eff} = l_\mathrm{n} + a_\mathrm{1} + a_\mathrm{2} = l_\mathrm{n} * 1,0 + l_\mathrm{n} * 0,025 + l_\mathrm{n} * 0,025\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}a_\mathrm{1} = a_\mathrm{2} = a_\mathrm{i}\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}a_\mathrm{i} = l_\mathrm{n} * 0,025\end{align}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align}l_\mathrm{n} = \cfrac{l_\mathrm{eff}}{1,05}\end{align}}

→ Daraus ergibt sich:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_\mathrm{i} = l_\mathrm{eff} * \cfrac{0,025}{1,05}}

Wobei:

a_i - Abstand des Auflagerpunktes vom Auflagerrand [cm]

b_A,B - Breite des linken/ rechten Auflagers [cm]

E - Einspannung des Auflagers [%]

l_eff - Effektive Stützweite [cm]

l_n - Lichter Abstand zwischen den Auflagerrändern

Quellen

Seiteninfo Status: überarbeitungsbedürftig Modul-Version: 2015.0240