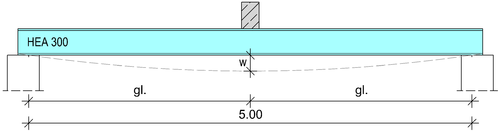
Auflagerelastizitäten (Bsp.)
Beispiel 1 Federsteifigkeit
Die folgende Rechnung ist beispielhaft für die Ermittlung der Federsteifigkeit eines Trägers. Das Beispiel ist modul-unabhängig.
Aufgabe
Im folgenden Beispiel wird ein Stahlbetonbalken auf einen Stahlträger (HEA 300) gelagert. Zur Bestimmung der Auflagerelastizität wird die Federsteifigkeit des Trägers ermittelt:
Vorgabewerte
Aus Nachschlagewerk[1] entnommene Werte:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I_\mathrm{y}=18260\,\mathrm{cm}^{4}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E=210000\,\mathrm{N}\mathrm{mm}^{-2}}
mit der Vorgabe einer selbst definierten Länge:
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l=5{,}00\,\mathrm{m}}
Berechnung
Durchbiegung unter einer Einzellast in Feldmitte
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w=\cfrac{F\cdot l^{3}}{48\cdot E\cdot I_\mathrm{y}}}
Federsteifigkeit
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\cfrac{F}{w} =\cfrac{\cancel{F}\cdot 48\cdot E\cdot I_\mathrm{y}}{\cancel{F}\cdot l^{3}}}
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k=\frac{ 48\cdot21000\,\mathrm{kNcm}^{ -2 }\cdot18260\,\mathrm{cm}^{ 4 }}{ (500\,\mathrm{cm})^{ 3 }}=147,249\,\frac{ \mathrm{kN} }{ \mathrm{cm} }=\underline{\underline{14724,9 \,\frac{ \mathrm{kN} }{ \mathrm{m} }}} }
Quellen
- ↑ [Schneider-2014] Albert, A (Hrsg.).: Schneider, Bautabellen für Ingenieure. 21. Auflage, Bundesamanzeiger Verlag, Köln 2014, ISBN 978-3-8462-0304-0
Seiteninfo
|