Stahlbetonstütze - Verfahren mit Nennkrümmung (Bsp.)

Veranschaulichung des Verfahrens mit Nennkrümmung

Dieses Berechnungsbeispiel verdeutlicht die Vorgehensweise bei der Bemessung einer Stahlbetonstütze nach dem Verfahren mit Nennkrümmung.

Handrechnung

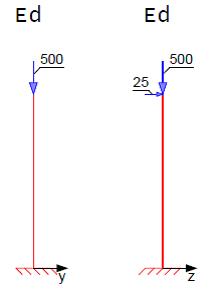
Einwirkungen

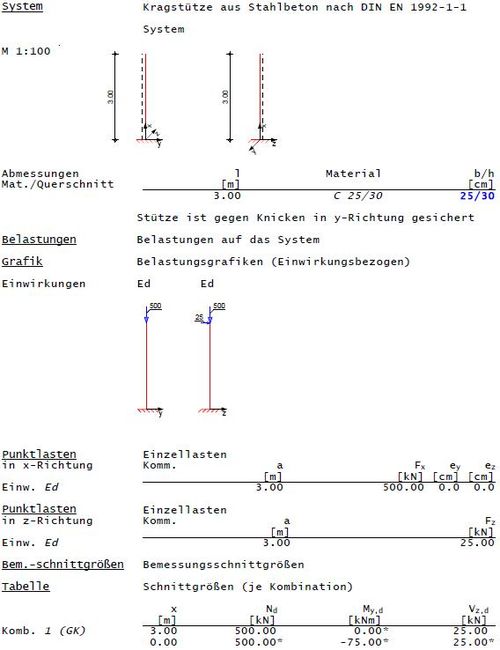
Querschnittsabmessungen, Betongüte und Endkriechzahl

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}b/h=25/30cm\quad \quad {{d}_{1}}=3,5cm\\l=3m\quad \quad \quad \quad \quad \quad C25/30\\\phi \left( \infty ,{{t}_{0}} \right)=2,0\end{array}}

In x-y-Ebene schließen Wände an, die Stütze ist in diese Richtung gehalten.

Schnittgrößen nach Theorie I. Ordnung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{N}_{Ed}}=-500kN\\{{M}_{y,Ed}}=25\cdot 3=75kNm\end{array}}

Schlankheitskriterium

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda =\frac{{{l}_{0}}}{{{i}_{y}}}=\frac{\beta \cdot {{l}_{col}}}{\sqrt{\frac{{{I}_{y}}}{A}}}=\frac{2\cdot 300}{\sqrt{\frac{(25\cdot 30{}^\text{3})/12}{25\cdot 30}}}=69,28}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{-500}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,47}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\lambda }_{\lim }}=25~}

Berücksichtigung von Einwirkungen nach Theorie II. Ordnung erforderlich.

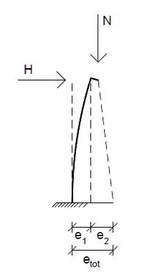
Planmäßige Ausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{0}}=\frac{{{M}_{Ed}}}{{{N}_{Ed}}}=\frac{75}{500}=0,15m}

Ungewollte Ausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}0\le {{\alpha }_{h}}=\frac{2}{{{l}^{0,5}}}\le 1\\{{\alpha }_{h}}=\frac{2}{{{3}^{0,5}}}=1,15\\{{\alpha }_{h}}=1\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{i}}={{\Theta }_{i}}\cdot \frac{{{l}_{0}}}{2}=\frac{1}{200\cdot {{\alpha }_{h}}}\cdot \frac{{{l}_{0}}}{2}=\frac{1}{200\cdot 1}\cdot \frac{6}{2}=0,015m}

Ausmitte nach Theorie II. Ordnung

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{\varphi }_{ef}}=\varphi \left(\infty ,{{t}_{0}}\right)\cdot {\frac {{M}_{0,Eqp}}{{M}_{0,Ed}}}=2\cdot {\frac {75}{75}}=2}

(wegen gegebener Bemessungswerte kann das Moment im GZG nicht genauer ermittelt werden)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta =0,35+\frac{{{f}_{ck}}}{200}-\frac{\lambda }{150}=0,35+\frac{25}{200}-\frac{69,28}{150}=0,013}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{K}_{\varphi }}=1+\beta \cdot {{\varphi }_{ef}}\ge 1\\{{K}_{\varphi }}=1+0,013\cdot 2=1,03\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{K}_{r}}=1~} (wegen vorerst unbekannter Bewehrung mit 1 angenommen)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{\varepsilon }_{yd}}=\frac{{{f}_{yd}}}{{{E}_{s}}}=\frac{500/1,15}{200000}=2,174\cdot {{10}^{-3}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{{{r}_{0}}}=\frac{{{\varepsilon }_{yd}}}{0,45\cdot d}=\frac{2,174\cdot {{10}^{-3}}}{0,45\cdot (0,3-0,035)}=0,0182{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}={{K}_{r}}\cdot {{K}_{\varphi }}\cdot \frac{1}{{{r}_{0}}}=1\cdot 1,03\cdot 0,0182=0,0188{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}=\frac{1}{r}\cdot l_{0}^{2}\cdot {{K}_{1}}\cdot \frac{1}{c}=0,0188\cdot 6{}^\text{2}\cdot 1\cdot \frac{1}{10}=0,0676m}

Gesamtausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}={{e}_{0}}+{{e}_{i}}+{{e}_{2}}=0,15+0,015+0,0676=0,2326m~}

Resultierendes Moment am Stützenfuß

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2,Ed}}={{N}_{Ed}}\cdot {{e}_{tot}}=500\cdot 0,2326=116,3kNm}

Bezogene Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=\frac{{{N}_{Ed}}}{b\cdot h\cdot {{f}_{cd}}}=\frac{-500}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=-0,47\\{{\mu }_{Ed}}=\frac{{{M}_{2,Ed}}}{b\cdot h{}^\text{2}\cdot {{f}_{cd}}}=\frac{11630}{25\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,36\end{array}}

Bemessung mit Interaktionsdiagramm für symmetrisch bewehrte Querschnitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{{{d}_{1}}}{h}=\frac{0,035}{0,3}=0,12\approx 0,1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\omega }_{tot}}=0,61\\{{A}_{s,tot}}={{\omega }_{tot}}\cdot \frac{b\cdot h}{{{f}_{yd}}/{{f}_{cd}}}=0,61\cdot \frac{25\cdot 30}{\frac{50}{1,15}/0,85\cdot \frac{2,5}{1,5}}=14,9cm{}^\text{2}\end{array}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{A}_{s1}}={{A}_{s2}}=\frac{14,9}{2}=7,35cm{}^\text{2}} , gewählt: 5ø14 je Seite, Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{A}_{s,vorh}}=7,7cm{}^{\text{2}}~}

Weitere Berechnung mit genauerem Krümmungsbeiwert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=\frac{{{N}_{Ed}}}{{{A}_{c}}\cdot {{f}_{cd}}}=-0,47}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega =\frac{{{A}_{s}}\cdot {{f}_{yd}}}{{{A}_{c}}\cdot {{f}_{cd}}}=\frac{2\cdot 7,7\cdot \frac{50}{1,15}}{25\cdot 30\cdot 0,85\cdot \frac{2,5}{1,5}}=0,63}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{n}_{u}}=1+\omega =1,63~}

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle {{K}_{r}}={\frac {{{n}_{u}}-n}{{{n}_{u}}-{{n}_{bal}}}}={\frac {1,63-0,47}{1,63-0,4}}=0,94}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{1}{r}={{K}_{r}}\cdot {{K}_{\varphi }}\cdot \frac{1}{{{r}_{0}}}=0,94\cdot 1,03\cdot 0,0182=0,0176{{m}^{-1}}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{2}}=\frac{1}{r}\cdot l_{0}^{2}\cdot {{K}_{1}}\cdot \frac{1}{c}=0,0176\cdot 6{}^\text{2}\cdot 1\cdot \frac{1}{10}=0,0634m}

Gesamtausmitte

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{e}_{tot}}={{e}_{0}}+{{e}_{i}}+{{e}_{2}}=0,15+0,015+0,0634=0,2284m~}

Resultierendes Moment am Stützenfuß

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {{M}_{2,Ed}}={{N}_{Ed}}\cdot {{e}_{tot}}=500\cdot 0,2284=114,22kNm}

Bezogene Schnittgrößen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{array}{l}{{\nu }_{Ed}}=-0,47\\{{\mu }_{Ed}}=\frac{{{M}_{2,Ed}}}{b\cdot h{}^\text{2}\cdot {{f}_{cd}}}=\frac{11422}{25\cdot 30{}^\text{2}\cdot 0,85\cdot \frac{2,5}{1,5}}=0,36\end{array}}

Keine wesentliche Veränderung, Bemessung bleibt bei 2x5ø14.
Anmerkung: die Berechnung mit dem Modul ergibt einen erforderlichen Querschnitt von 0,02cm² über den vorhandenen mit 10ø14 an und verlangt daraufhin 2 weitere Stäbe.

mb-Berechnung

Quellen

Seiteninfo Status: Seite fertig, ungeprüft