Elementdecken - Bemessungsbeispiel: Unterschied zwischen den Versionen
MExner (Diskussion | Beiträge) |
MExner (Diskussion | Beiträge) |
||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 287: | Zeile 287: | ||
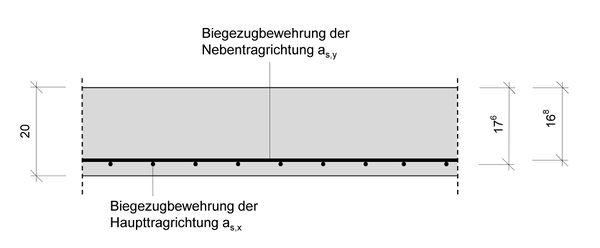
Es wird angenommen, dass die Bewehrungslage der Haupttragrichtung sinnvollerweise außen angeordnet wird (größerer Hebelarm der inneren Kräfte). | Es wird angenommen, dass die Bewehrungslage der Haupttragrichtung sinnvollerweise außen angeordnet wird (größerer Hebelarm der inneren Kräfte). | ||
<br/><br/> | <br/><br/> | ||
| − | + | ::[[Datei:Elementdecken-Bemessungsbeispiel 8.jpg|none|thumb|600px|Bewehrungsanordnung monolithisch hergestellte Ortbetondecke]] | |
| − | + | <br/><br/> | |
| − | |||
:: <math> c_{\,V}=20\,\,mm </math> <br/><br/> | :: <math> c_{\,V}=20\,\,mm </math> <br/><br/> | ||
:: <math> \varnothing_{s,x} = \varnothing_{s,y} = 8\,\,mm </math> <br/><br/> | :: <math> \varnothing_{s,x} = \varnothing_{s,y} = 8\,\,mm </math> <br/><br/> | ||
| Zeile 296: | Zeile 295: | ||
:: <math> d_{1,y} = c_{\,V} + \varnothing_{s,x} + 0,5 * \varnothing_{s,y} = 20\,\,mm + 8\,\,mm + 0,5 * 8\,\,mm = 32\,\,mm </math> <br/><br/> | :: <math> d_{1,y} = c_{\,V} + \varnothing_{s,x} + 0,5 * \varnothing_{s,y} = 20\,\,mm + 8\,\,mm + 0,5 * 8\,\,mm = 32\,\,mm </math> <br/><br/> | ||
:: <math> d_y = h - d_{1,y} = 200\,\,mm - 32\,\,mm = 168\,\,mm </math><br/><br/> | :: <math> d_y = h - d_{1,y} = 200\,\,mm - 32\,\,mm = 168\,\,mm </math><br/><br/> | ||
| − | + | ||
| − | |||
| − | |||
:: <math> \mu_{Eds,i} = \frac{m_{Eds,i}} {b * d_{i}^{\,2} * f_{cd}} </math><br/><br/> | :: <math> \mu_{Eds,i} = \frac{m_{Eds,i}} {b * d_{i}^{\,2} * f_{cd}} </math><br/><br/> | ||
:: <math> m_{Eds,i} = m_{Ed,i}\,\,\,\,(n_{Ed,i} = 0 ) </math><br/><br/> | :: <math> m_{Eds,i} = m_{Ed,i}\,\,\,\,(n_{Ed,i} = 0 ) </math><br/><br/> | ||
| Zeile 315: | Zeile 312: | ||
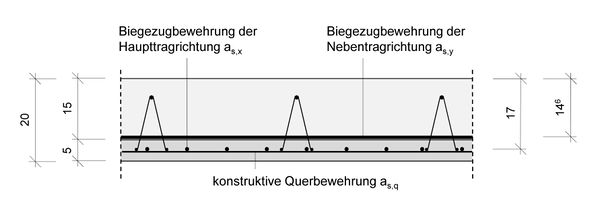
:* die Biegezugbewehrung der Nebentragrichtung wird auf dem Halbfertigteil angeordnet und liegt dadurch 22 mm weiter oben<br/> | :* die Biegezugbewehrung der Nebentragrichtung wird auf dem Halbfertigteil angeordnet und liegt dadurch 22 mm weiter oben<br/> | ||
<br/> | <br/> | ||
| + | ::[[Datei:Elementdecken-Bemessungsbeispiel 9.jpg|thumb|none|600px|Bewehrungsanordnung Elementdecke]] | ||
| + | <br/><br/> | ||
:: <math> c_{\,V}=20\,\,mm </math> <br/><br/> | :: <math> c_{\,V}=20\,\,mm </math> <br/><br/> | ||
:: <math> \varnothing_{s,q} = 6\,\,mm\,\,(konstruktive\,\,Querbewehrung)</math> <br/><br/> | :: <math> \varnothing_{s,q} = 6\,\,mm\,\,(konstruktive\,\,Querbewehrung)</math> <br/><br/> | ||
| Zeile 371: | Zeile 370: | ||
Es ergeben sich für das Beispiel folgende Werte:<br/> | Es ergeben sich für das Beispiel folgende Werte:<br/> | ||
<br/> | <br/> | ||
| − | :<math> neu\,\,a_{s,x}=2,60\,\,cm^2/m*\frac{17, | + | :<math> neu\,\,a_{s,x}=2,60\,\,cm^2/m*\frac{17,6\,\,cm}{17,0\,\,cm} = \underline{\underline{2,69\,\,cm^2/m}}</math><br/><br/> |
:<math> neu\,\,a_{s,y}=1,45\,\,cm^2/m*\frac{16,8\,\,cm}{14,6\,\,cm} = \underline{\underline{1,67\,\,cm^2/m}}</math><br/><br/> | :<math> neu\,\,a_{s,y}=1,45\,\,cm^2/m*\frac{16,8\,\,cm}{14,6\,\,cm} = \underline{\underline{1,67\,\,cm^2/m}}</math><br/><br/> | ||
| Zeile 409: | Zeile 408: | ||
Der Nachweis der Verbundfuge ist für die Beanspruchung in dieser Tragrichtung offensichtlich erbracht. | Der Nachweis der Verbundfuge ist für die Beanspruchung in dieser Tragrichtung offensichtlich erbracht. | ||
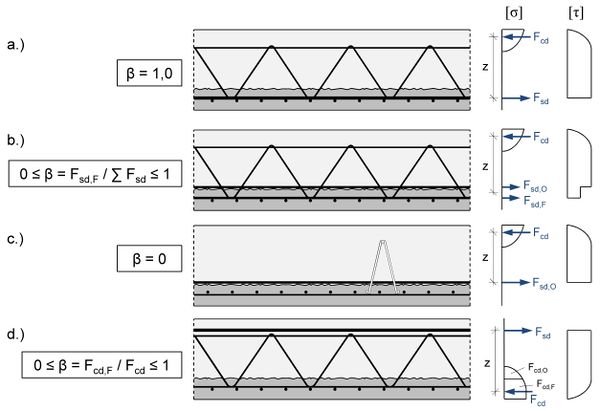
| − | In der Hauptragrichtung ergibt sich an den Endauflagern ein Verhältniswert von β = 1,0 (Abbildung Buchstabe a). | + | In der Hauptragrichtung ergibt sich an den Endauflagern ein Verhältniswert von ''β = 1,0'' (Abbildung Buchstabe a). |
| − | + | Die maximale einwirkende Querkraft befindet sich jedoch am Zwischenauflager. Dort müsste bei genauer Betrachtung berechnet werden, welcher Anteil der Betondruckzone sich im Halbfertigteil befindet und ins Verhältnis zur gesamten Betondruckzone gesetzt werden (Abbildung Buchstabe d). | |
| − | Vereinfachend und auf der sicheren Seite liegend wird auch hier ein Verhältniswert von β = 1,0 angesetzt (volle Schubübertragung durch die Verbundfuge). | + | Vereinfachend und auf der sicheren Seite liegend wird auch hier ein Verhältniswert von ''β = 1,0'' angesetzt (volle Schubübertragung durch die Verbundfuge). |
| − | + | ||
| + | Für den Nachweis am Zwischenauflager wird vereinfachend ebenfalls eine statische Nutzhöhe von ''d = 170 mm'' angenommen. | ||
Der Hebelarm der inneren Kräfte wird mit ''z = 0,9 * d'' bestimmt (keine Querkraftbewehrung erforderlich). | Der Hebelarm der inneren Kräfte wird mit ''z = 0,9 * d'' bestimmt (keine Querkraftbewehrung erforderlich). | ||
Die einwirkende Schubkraft ergibt sich folgendermaßen:<ref name="Technische Information Filigran"/> | Die einwirkende Schubkraft ergibt sich folgendermaßen:<ref name="Technische Information Filigran"/> | ||
<br/><br/> | <br/><br/> | ||
| − | :<math>v_{Edi} = \frac{\beta * v_{Ed}}{z* | + | :<math>v_{Edi} = \frac{\beta * v_{Ed}}{z*b_{i}}</math><br/><br/> |
:{| | :{| | ||
| Zeile 428: | Zeile 428: | ||
|<math>z</math>||... Hebelarm der inneren Kräfte | |<math>z</math>||... Hebelarm der inneren Kräfte | ||
|- | |- | ||
| − | |<math> | + | |<math>b_{i}</math>||... wirksame Breite der Verbundfuge |
|}<br/><br/> | |}<br/><br/> | ||
Aktuelle Version vom 1. August 2020, 11:11 Uhr
Aufgabenstellung
Die Bemessung von Elementdecken soll anhand des folgenden Beispiels veranschaulicht werden.
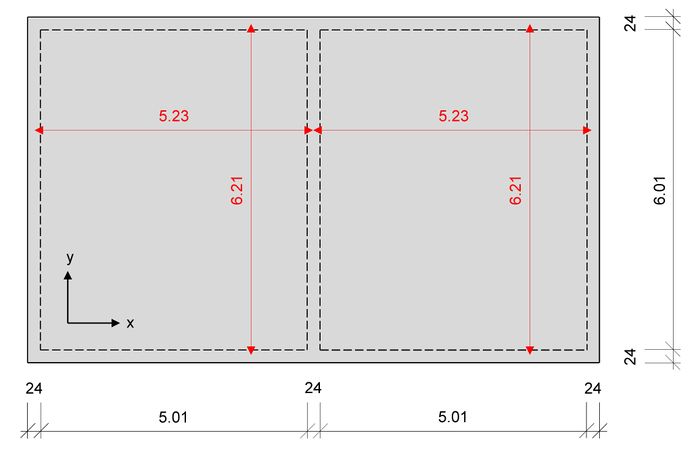
Es handelt sich dabei um eine zweiachsig gespannte Durchlaufplatte über dem dargestellten Grundriss.
Die rechnerischen Spannweiten wurden bereits ermittelt und im Grundriss angegeben.
Außerdem sind die folgenden Paramater und Bemessungschnittgrößen (nach Czerny) für die Bemessung bekannt:
- Deckenstärke h=20 cm
- Dicke des Halbfertigteils hP = 50 mm
- Halbfertigteil und Ortbeton aus C25/30
- Expositionsklasse XC 1 (Innenbauteil)
- raue Oberfläche der Verbundfuge
- Bewehrungsanordnung:
- Biegezugbewehrung der Hauptragrichtung und konstruktive Querbewehrung inkl. Abstandhalter im Halbfertigteil,
- Biegezugbewehrung der Nebentragrichtung vollständig im Ortbeton,
- direkte Verlegung der bauseitigen Zulagen auf den Halbfertigteilen
- Stabdurchmesser:
- Biegezugbewehrung Øs 8 mm
- konstruktive Querbewehrung Øs 6 mm
Bemessungsschnittgrößen in x-Richtung (Haupttragrichtung) max. Feldmoment m x,F = + 19,5 kNm/m Stützmoment m x,S = - 44,00 kNm/m Querkraft am Endauflager q x,A = +/- 29,95 kN/m Querkraft am Zwischenauflager q x,B = +/- 52,65 kN/m in y-Richtung (Nebentragrichtung) max. Feldmoment m y,F = + 10,62 kNm/m Querkraft am Endauflager q y,A = +/- 25,67 kN/m
Bemessung für den Montagezustand
Elementierung
Die Bemessung für den Montagezustand beginnt mit der Einteilung des Deckengrundrisses in Elemente (Elementierung). Dabei sind die Anwendungsregeln nach Eurocode 2 und den Zulassungen zu beachten (siehe Seite Elementdecken - Anwendungsregeln - Abschnitt Abmessungen Halbfertigteil, Aufbetonschicht und Gesamtdecke). Dieses betrifft insbesondere folgende Punkte:
- mögliche Elementabmessungen und -massen (Kosten)
- Passplattenanteil (Kosten)
- Lage von Stoßfugen (Drillsteifigkeit)
- Auflagerung der Halbfertigteile (Randunterstützungen, Mörtelbettauflagerung, Auflagerpressung)
- Anordnung der Gitterträger (Tragrichtung, Lastverteilung)
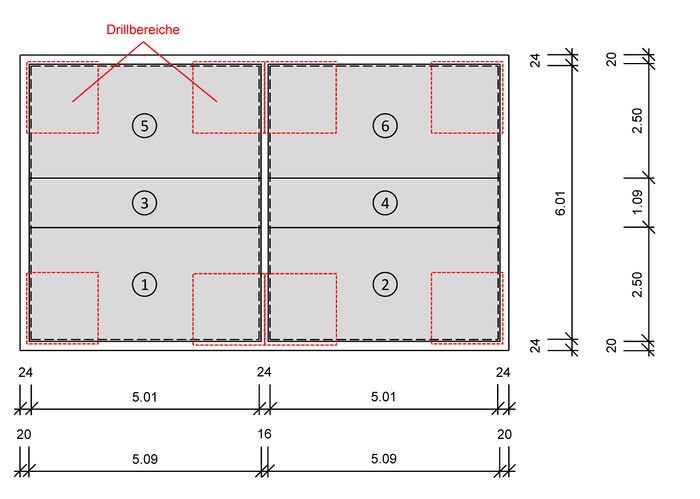
Unter Berücksichtigung der genannten Punkte, wird die dargestellte Elementierung gewählt.
Diese besteht aus zwei Passplatten (Pos. 3 und 4) und vier Standardbreiten ( Pos. 1, 2, 5, 6).
Die Stoßfugen wurden aus den Drillbereichen ferngehalten, um eine Verringerung der Drillsteifgkeit auszuschließen.
Außerdem wurde eine allseitige Auflagerung der Halbfertigteile von 40 mm gewählt um eine trockene Auflagerung auf dem Geschossmauerwerk zu ermöglichen.
Eine Begrenzung der maximalen Auflagerpressung entsprechend Eurocode 2 ist im Weiteren zu beachten bzw. nachzuweisen.
Die Abmessungen der einzelnen Elemente (Positionen) können der Abbildung entnommen werden. Diese müssen zusammen mit den Einzelmassen der Positionen im Verlegeplan angegeben werden.
Die Massen der Positionen werden folgendermaßen berechnet:
mit:
... Einzelmasse der Position ... Länge der Position ... Breite der Position ... Dicke der Position ... Dichte Stahlbeton (2,5 to/m³)
Es ergeben sich die folgenden Einzelmassen der Positionen.
- Positionen 1 - 6 (Platten mit einer Standardbreite von 2,50 m):
- Positionen 3 und 4 (Passplatten mit einer von Breite 1,09 m):
Gitterträgerwahl
Die Wahl der Gitterträger erfolgt in Abhängigkeit von der Funktion und der Auslastung der Decke.
Im vorliegenden Beispiel sollen Standardgitterträger verwendet werden. Diese sollen die Tragfähigkeit im Montagezustand (Montagegitterträger) sicherstellen und im Endzustand als Verbundbewehrung anrechenbar sein.
Auf die sich bereits daraus ergebenden Anforderungen an die erforderliche Gitterträgerhöhe wird auf der Seite Elementdecken - Anwendungsregeln - Abschnitt Gitterträgerhöhen eingegangen.
Auf die verschiedenen Gitterträgertypen und Anwendungsbereiche wird auf der Seite Gitterträger nach Zulassung eingegangen.
Die Entwurfshöhe der Gitterträger kann tabellarisch bestimmt werden:
| Deckenhöhe | + 200 mm |
| obere Betondeckung (XC 1) | - 20 mm |
| obere Bewehrungslage | - 20 mm |
| konstrukive Querbewehrung im Halbfertigteil | - 6 mm |
| untere Betondeckung (XC 1) | - 20 mm |
| verbleibende Bauhöhe | + 134 mm |
| gew. Gitterträger-Entwurfshöhe | 130 mm |
|---|
Es wird ein Standard-Gitterträger Typ E der Fa. Filigran (Zulassung Z-15.1-147) mit der folgenden Stabkonfiguration gewählt:
- - gerippte Untergurte Øs = 6 mm
- - glatte Diagonalen Øs = 6 mm
- - glatter Obergurt Øs = 10 mm
Die Bezeichnung der Gitterträger erfolgt entsprechend geltenden Vereinbarungen nach folgendem Schema:[1]
- Gitterträgertyp Entwurfshöhe - Untergurtdurchmesser Diagonalendurchmesser Obergurtdurchmesser
Zu beachten ist, dass Untergurt- und Obergurtdurchmesser stets mit jeweils zwei Ziffern zu beschreiben sind, auch bei Durchmessern kleiner 10 mm. Beim Diagonalendurchmesser genügt eine Ziffer, da die verfügbaren Diagonalendurchmesser immer im einstelligen Millimeterbereich liegen.
Für den gewählten Gitterträger ergibt sich folgende Bezeichnung:
- E 13 - 06 6 10
Gitterträgeranordnung
Bei der Anordnung der Gitterträger sind insbesondere folgende Punkte zu beachten (siehe Seite Elementdecken - Anwendungsregeln - Abschnitt Gitterträgeranordnung)
- maximale Gitterträgerabstände in Abhängigkeit von der Funktion (Montagegitterträger/ Verbundbewehrung/ Querkraftbewehrung)
- maximale Abstände zu Elementrändern
- Mindestbestückung bei Passplatten
- gleichmäßige, möglichst symmetrische Verteilung
- Knotenanordnung über Auflagern (Randunterstützungen)
Im vorliegenden Beispiel sollen die Montagegitterträger als Verbundbewehrung anrechenbar sein.
Der Querabstand der Gitterträger untereinander ist daher auf 75 cm und zu Elementrändern auf 37,5 cm begrenzt. Außerdem sind die Passplatten breiter als 37,5 cm und müssen daher mindestens zwei Gitterträger erhalten.
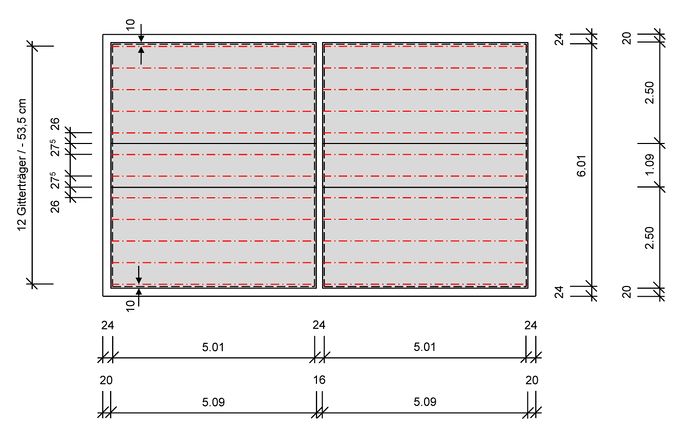
Es werden daher 12 Gitterträger gleichmäßig über den Deckengrundriss verteilt. Es ergibt sich ein konstanter Gitterträgerabstand von 53,5 cm. Die Abstände der Gitterträger zu Elementrändern ergeben sich ebenfalls und können der Abbildung entnommen werden.
Sowohl die Gitterträgerabstände untereinander, als auch die Abstände zu Elementrändern ermöglichen eine Anrechenbarkeit als Verbundbewehrung.
Die Gitterträger enden im Halbfertigteil. Die Länge wird auf 5,07 m festgelegt.
Begrenzung der Montagestützweite
Die eigentliche Bemessung für den Montagezustand erfolgt durch Begrenzung der Abstände zwischen den Montageunterstützungen (Montagestützweiten). Auf Erläuterungen zum Tragverhalten und zur Systembildung für die Berechnung wird auf der Seite Elementdecken - Tragverhalten und Bemessung - Abschnitt Bemessung für den Montagezustand eingegangen.
In diesem Beispiel soll der Nachweis durch Verwendung der in Bemessungshilfen tabellierten zulässigen Montagestützweiten gezeigt werden.
Für den gewählten Gitterträger stellt der Hersteller (Filigran Trägersysteme GmbH & Co. KG) eine Bemessungshilfe, die FI-Norm E-1-2100, zur Verfügung.
Dieser können die zulässigen Montagestützweiten für bestimmte Obergurt- und Diagonalendurchmesser in Abhängigkeit vom Trägerabstand, der Trägerhöhe und der Deckenhöhe entnommen werden.
Bei niedrigen Gitterträgern mit Obergurtdurchmessern bis 10 mm sind besondere Regelungen zu beachten, wenn im Montagezustand keine günstige Durchlaufwirkung an Zwischenunterstützungen zu erwarten ist (Klammerwerte).
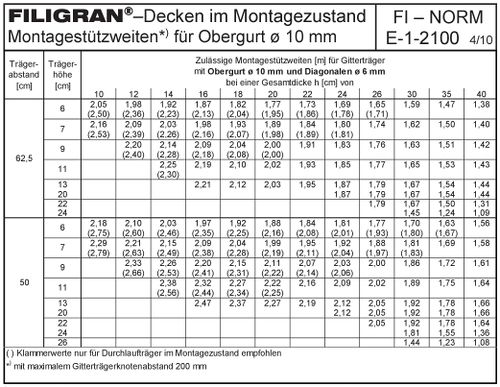
Der im Beispiel festgelegte Gitterträgerabstand von 53,5 cm ist nicht tabelliert. Die zulässige Montagestützweite kann in diesem Fall vereinfachend für den nächstgrößeren Trägerabstand aus der FI-Norm abgelesen oder linear interpoliert werden.
In diesem Fall soll vereinfachend der nächstgrößere Trägerabstand angesetzt werden. Für einen Trägerabstand von 62,5 cm, eine Trägerhöhe von 13 cm und eine Deckendicke von 20 cm ergibt sich eine zulässige Montagestützweite von 2,03 m. Besonderheiten bezüglich einer vorhandenen oder nicht vorhandenen Durchlaufwirkung sind bei der gewählten Trägerhöhe nicht zu beachten.
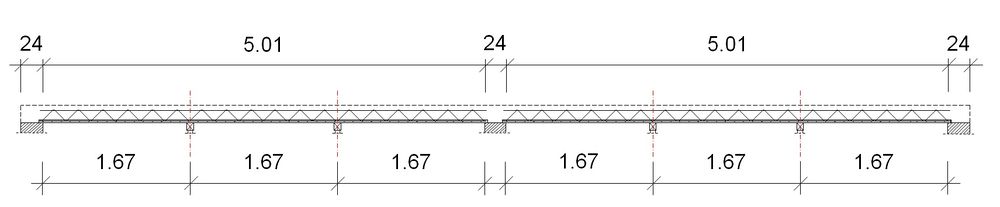
Die zulässige Montagestützweite von 2,03 m ist bei einer lichten Weite zwischen den Auflagerwänden von 5,01 m nicht ausreichend um lediglich mit einer mittigen Unterstützungsreihe auszukommen. Es werden daher zwei Unterstützungsreihen in den Drittelpunkten der lichten Deckenspannweite angeordnet. Es ergibt sich eine vorhandene Montagestützweite von 1,67 m.
Grundsätzlich sind an Wandauflagern zusätzliche Randunterstützungen für den Montagezustand anzuordnen. Diese dürfen unter Einhaltung bestimmter Bedingungen entfallen (Mindestauflagertiefe und Knotenanordnung über den Auflagern). Die gewählte Auflagertiefe ist mit 40 mm größer als 35 mm und die erste Bedingung somit erfüllt. Für die Überprüfung der zweiten Bedingung (Knotenanordnung über den Auflagern) muss die Auflagerkraft je Gitterträger für die vorhandene Montagestützweite und den vorhandenen Gitterträgerabstand ermittelt werden.
Die Berechnung der vorhandenen Auflagerkraft je Gitterträger kann durch Umstellung der Formeln erfolgen, welche für die Berechnung der zulässigen Montagestützweite aus der zulässigen Querkraft in Bemessungshilfen enthalten sind.
Da die Formeln für die Berechnung der Stützweite am Einfeldsystem gelten, entspricht die Querkraft beträgsmäßig der Auflagerkraft.
Durch gleichsetzen von zul. V = vorh. V und zul. l M = vorh. l M ergeben sich die folgenden Formeln für die Berechnung der Auflagerkraft je Gitterträger.
Auflagerlast je Gitterträger unter Eigenlast + Flächenlast (Nutzlast):
Auflagerlast je Gitterträger unter Eigenlast + Einzellast (Nutzlast) am Auflager:
mit:
... vorhandene Auflagerkraft je Gitterträger [kN] ... vorhandene Querkraft je Gitterträger [kN] ... vorhandene Montagestützweite [m] ... Eigenlast der Decke (Fertigteil + Ortbeton) [kN/m²] ... Flächenlast (Nutzlast) [kN/m²] ... Einzellast (Nutzlast) [kN] ... Gitterträgerabstand [m]
Für das Beispiel ergeben sich folgende Werte:
Auflagerlast je Gitterträger unter Eigenlast + Flächenlast (Nutzlast):
Auflagerlast je Gitterträger unter Eigenlast + Einzellast (Nutzlast) am Auflager:
Da die Auflagerkräfte je Gitterträger kleiner/gleich 5,0 kN sind, darf auf zusätzliche Randunterstützungen im Montagezustand verzichtet werden, wenn entlang der Auflagerlinie jeder zweite Gitterträger so angeordnet wurde, dass sich ein Untergurtknoten über dem Auflager befindet. Dieses ist bereits bei der Herstellung der Halbfertigteile im Betonfertigteilwerk zu beachten und vor der Verlegung der Halbfertigteile zu kontrollieren.
Die Anordnung der Montageunterstützungen und die Lage der Bezugspunkte für die Montagestützweite kann der Abbildung entnommen werden.
Mindestlängsbewehrung
Um ein Reißen des Zuggurtes (Beton, Gitterträgeruntergurte, Zulagebewehrung im Halbfertigteil) noch vor dem Ausknicken des Gitterträgerobergurtes zu vermeiden, müssen die Halbfertigteile einen Längsbewehrungsquerschnitt aufweisen.
Dieser Mindestlängsbewehrungsquerschnitt kann den Zulassungen oder Bemessungshilfen entnommen werden. Vereinfacht kann der erforderliche Bewehrungsquerschnitt unter der Annahme berechnet werden, dass Zug- und Druckgurt betragsmäßig die gleichen Kräfte aufnehmen. Die Berechnung erfolgt mit der unten dargestellten Formel.[1]
mit:
... erfordeliche Mindestlängsbewehrung je Gitterträgerobergurt [cm²] ... globaler Sicherheitsbeiwert 1,75 ... zulässiges Moment aus Gitterträgerzulassung [kNcm] ... Entwurfshöhe des Gitterträgers (UK UG bis OK OG) [cm] ... charakteristische Streckgrenze der Gitterträgeruntergurte bzw. Zulagebewehrung [kN/cm²]
Bei einer Trägerhöhe von 13 cm und einem Obergurtdurchmesser von 10 mm ergibt sich gemäß der entsprechenden Zulassung des gewählten Gitterträgers (Z-15.1-147) ein zulässiges Moment von 2,10 kNm je Gitterträger.
Es ergibt sich ein erforderlicher Mindestlängsbewehrungsquerschnitt zu:
Die Gitterträgeruntergurte (2 Ø 6 = 0,57 cm²) decken den erforderlichen Mindestlängsbewehrungquerschnitt bereits fast vollständig ab.
Da die vorhandene Stützweite kleiner als die maximal zulässige Stützweite ist, wird das zulässige Moment nicht ausgereizt.
Es kann daher davon ausgegangen werden, dass die Gitterträgeruntergurte allein ausreichend sind, um das Biegetragverhalten im Montagezustand sicherzustellen.
Wären die Gitterträgeruntergurte nicht ausreichend, könnte die im Halbfertigteil verlegte Biegezugbewehrung, die für den Endzustand erforderlich ist, angerechnet werden.
Mindestquerbewehrung (konstruktiv)
Um eine ausreichende Biegesteifigkeit über die Elementbreite (quer zu den Gitterträgern) im Montagezustand sicherzustellen, ist konstruktiv eine Mindestquerbewehrung einzulegen. Dieses wird in diesem Beispiel durch Ø 6 im maximalen Abstand von 25 cm gewährleistet. Im Betonfertigteilwerk wird die konstruktive Querbewehrung teilweise inkl. vormontierter Abstandhalter als erstes auf den Fertigungstischen positioniert und darauf die Gitterträger und weiteren Zulagen angeordnet.
Bemessung für den Endzustand
Biegebemessung und Vergleich der Ergebnisse
Die Biegebemessung von Elementdecken erfolgt in der Regel auf Grundlage einer statischen Berechnung für eine monolithisch hergestellte Ortbetondecke (Ortbetonstatik) durch den Hersteller der Elementdecke. Wenn jedoch bereits in den frühen Planungsphasen feststeht, dass die Decken als Elementdecken ausgeführt werden sollen, können diese auch gleich als solche bemessen werden.
Um die verschiedenen Berechnungsmöglichkeiten zu zeigen und einen Vergleich der Ergebnisse zu ermöglichen, soll die Biegebemessung der Decke in diesem Beispiel in den nachfolgenden drei Schritten erfolgen:
Auf weiterführende Nachweise wie z.B. Betondeckungmaße, maximale Stababstände, Verankerung der Bewehrung, Übergreifungslängen, Mindestbewehrung zur Sicherstellung der Duktilität usw. wird an dieser Stelle nicht eingegangen. Es gelten im Wesentlichen die gleichen Regelungen wie bei Ortbetondecken. Auf Besonderheiten z.B. bei der erforderlichen Betondeckung zur Verbundfuge, beim Nachweis der Verankerung der Bewehrung an Endauflagern oder bei Bewehrungsanordnungen mit gestoßener Biegebewehrung wird u.A. auf den Seiten Elementdecken - Anwendungsregeln und Betondeckung - Abschnitt Betondeckungsmaße bei Halbfertigteilen eingegangen.
Bemessung als monolithisch hergestellte Ortbetondecke
Die Bemessung der Biegezugbewehrung für die maximalen Feldmomente in x- und y-Richtung (siehe Aufgabenstellung) erfolgt mit dem Omega-Verfahren (Schneider Bautabellen (23. Auflage) Tafel 2a. [3]
Es wird angenommen, dass die Bewehrungslage der Haupttragrichtung sinnvollerweise außen angeordnet wird (größerer Hebelarm der inneren Kräfte).
Vollständige Neubemessung unter Berücksichtigung der geänderten statischen Nutzhöhen
Bei der vollständigen Neubemessung erfolgt die Berechnung analog zur ersten Variante jedoch mit dem Unterschied, dass sich die Höhenlagen der Bewehrung und somit die statischen Nutzhöhen in ungünstiger Weise ändern:
- die Biegezugbewehrung der Hauptragrichtung liegt auf der konstruktiven Querbewehrung im Halbfertigteil und dadurch 6 mm weiter oben
- die Biegezugbewehrung der Nebentragrichtung wird auf dem Halbfertigteil angeordnet und liegt dadurch 22 mm weiter oben
Umbemessung auf Grundlage der Ortbetonstatik durch lineare Erhöhung der Bewehrungsquerschnitte
Die Umbemessung auf Grundlage der Ortbetonstatik erfolgt durch lineare Erhöhung der erforderlichen Bewehrungsquerschnitte um das Verhältnis der statischen Nutzhöhen.
Eine Anpassung erfolgt dabei in der Regel nur für die Bewehrungslage im Ortbeton. Um einen vollständigen Vergleich der Ergebnisse zu ermöglichen, wird auch der Bewehrungsquerschnitt im Halbfertigteil linear erhöht.
Folgende Werte werden für die Umbemessung benötigt:
| Werte aus der Ortbetonstatik | reduzierte statische Nutzhöhe in der Elementdecke | ||
|---|---|---|---|
Die Berechnung der neuen erforderlichen Bewehrungsquerschnitte erfolgt mit der Formel:
wobei:
... neuer erforderlicher Bewehrungsquerschnitt der Tragrichtung i (Elementdecke) ... erforderlicher Bewehrungsquerschnitt der Tragrichtung i (Ortbetonstatik) ... statische Nutzhöhe der Tragrichtung i (Ortbetonstatik) ... statische Nutzhöhe der Tragrichtung i (Elementdecke)
Es ergeben sich für das Beispiel folgende Werte:
Vergleich der Ergebnisse
Allgemein ist zu erkennen, dass sich bei der Ausführung als Elementdecke höhere erforderliche Bewehrungsgrade ergeben. Dieses betrifft insbesondere die Bewehrung, welche im Ortbeton verlegt wird. In diesem Beispiel trifft dieses nur für die Bewehrung der Nebentragrichtung zu, bei anderen Bewehrungsanordnungen gilt dieses auch für Stoßzulagen im Ortbeton.
Ein Vergleich der Ergebnisse der vollständigen Neubemessung und der vereinfachten linearen Erhöhung der Bewehrungsquerschnitte zeigt, dass sich bei der linearen Erhöhung geringfügig geringere erforderliche Bewehrungsquerschnitte ergeben. Für übliche Standardanwendungen wird dieses Verfahren jedoch als ausreichend genau angesehen.[1]
Die folgende Tabelle zeigt einen prozentualen Vergleich der erforderlichen Bewehrungsquerschnitte die sich aus den verschiedenen Berechnungsverfahren ergeben (Bezugwert ist je Tragrichtung die Ausführung als monolithisch hergestellte Ortbetondecke).
| Monolitisch hergestellte Ortbetondecke | Elementdecke | ||
|---|---|---|---|
| Neubemessung | lineare Erhöhung | ||
Nachweis der Verbundfuge
Einwirkende Schubspannung
Die Tragfähigkeit der Verbundfuge ist für die einwirkende Schubkraft nachzuweisen. Die einwirkende Schubkraft ist abhängig von der Bewehrungsanordnung und wird mit Hilfe des Verhältniswertes β bestimmt. Auf die Bedeutung dieses Wertes wird auf der Seite Elementdecken - Tragverhalten und Bemessung - Abschnitt Einwirkende Schubspannung eingegangen.
Da in vorliegendem Beispiel die Bewehrung der Nebentragrichtung vollständig im Ortbeton liegt, ist der Verhältniswert β für die Nebentragrichtung gleich Null (Abbildung Buchstabe c). Der Nachweis der Verbundfuge ist für die Beanspruchung in dieser Tragrichtung offensichtlich erbracht.
In der Hauptragrichtung ergibt sich an den Endauflagern ein Verhältniswert von β = 1,0 (Abbildung Buchstabe a). Die maximale einwirkende Querkraft befindet sich jedoch am Zwischenauflager. Dort müsste bei genauer Betrachtung berechnet werden, welcher Anteil der Betondruckzone sich im Halbfertigteil befindet und ins Verhältnis zur gesamten Betondruckzone gesetzt werden (Abbildung Buchstabe d). Vereinfachend und auf der sicheren Seite liegend wird auch hier ein Verhältniswert von β = 1,0 angesetzt (volle Schubübertragung durch die Verbundfuge).
Für den Nachweis am Zwischenauflager wird vereinfachend ebenfalls eine statische Nutzhöhe von d = 170 mm angenommen. Der Hebelarm der inneren Kräfte wird mit z = 0,9 * d bestimmt (keine Querkraftbewehrung erforderlich).
Die einwirkende Schubkraft ergibt sich folgendermaßen:[2]
... Bemessungswert der einwirkenden Schubkraft in der Verbundfuge (Index i für "Interface" - dt.: Schnittstelle) ... Verhältniswert der einwirkenden Schubkraft in der Verbundfuge ... Bemessungswert der einwirkenden Querkraft je Meter ... Hebelarm der inneren Kräfte ... wirksame Breite der Verbundfuge
Schubwiderstand
Der Tragwiderstand der Verbundfuge wird nach den Zulassungen und Eurocode 2 folgendermaßen bestimmt. [2] [4]
wobei:
... maßgebender Bemessungswert der aufnehmbaren Schubkraft in der Verbundfuge ... Bemessungswert der Schubtragfähigkeit der Verbundfuge ohne Verbundbewehrung ... Bemessungswert der Schubtragfähigkeit der Verbundbewehrung ... Obergrenze des Bemessungswertes der Schubtragfähigkeit der Verbundfuge nach EC2-1-1, 6.2.5 (1) ... Obergrenze des Bemessungswertes der Schubtragfähigkeit der Verbundfuge nach Zulassung ... Betondruckfestigkeit ... Betonzugfestigkeit ... Streckgrenze der Verbundbewehrung ... Verbundbewehrungsgrad (Querschnittsfläche der Verbundbewehrung je m² Verbundfugenoberfläche ... Neigung der Verbundbewehrung (Diagonalen mit 35° ≤ α ≤ 90°)
In die Bemessung gehen an verschiedenen Stellen die Rauigkeitsbeiwerte ein, welche in Abhängigkeit von der Oberflächenbeschaffenheit der Verbundfuge der folgenden Tabelle entnommen werden können:[2]
Fugenbeschaffenheit glatt 0,2 0,6 0,2 rau 0,4 0,7 0,5
wobei:
... Rauigkeitsbeiwert für den Adhäsionstraganteil ... Rauigkeitsbeiwert für den Reibungstraganteil ... Rauigkeitsbeiwert zur Abminderung der Betonfestigkeit
Die Schubtragfähigkeit der Verbundfuge ohne Verbundbewehrung kann für die Betongüte C25/30 bei rauer Fuge mit vRdi,c = 0,408 N/mm² aus dem folgenden Tabellenauszug aus der Bemessungshilfe [2] abgelesen werden.
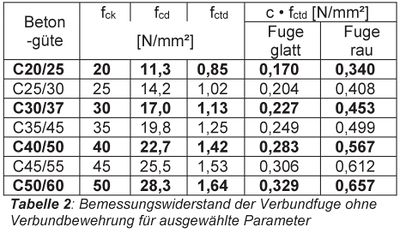 Bemessungswiderstand der Verbundfuge ohne Verbundbewehrung - Auszug aus FI – Norm-2-4539 [2]
Bemessungswiderstand der Verbundfuge ohne Verbundbewehrung - Auszug aus FI – Norm-2-4539 [2]
Der Traganteil der Verbundbewehrung könnte mit der oben dargestellten Formel für jeden Gitterträger berechnet werden.
Dafür ist unter anderem die Kenntnis der Diagonalenneigung α erforderlich. Der Gitterträgerabstand geht über den Verbundbewehrungsgrad in die Berechnung ein.
In diesem Beispiel sollen statt der Berechnung die Tabellenwerte aus den Bemessungshilfen verwendet werden.
Dem folgenden Tabellenauszug für eine raue Verbundfuge kann auf der sicheren Seite liegend der Wert für eine Trägerhöhe von 150 mm und einen Trägerabstand von 55 cm abgelesen werden und beträgt vRdi,s = 0,23 N/mm².
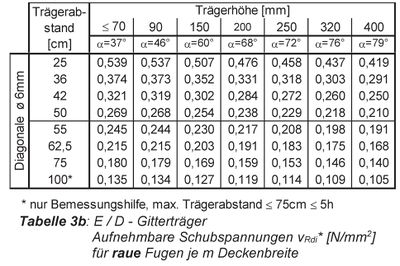 Bemessungswiderstand der Schubtragfähigkeit der Verbundbewehrung bei rauer Fuge - Auszug aus FI – Norm-2-4539 [2]
Bemessungswiderstand der Schubtragfähigkeit der Verbundbewehrung bei rauer Fuge - Auszug aus FI – Norm-2-4539 [2]
Die Obergrenze des Bemessungswertes der Schubtragfähigkeit der Verbundfuge nach EC2-1-1, 6.2.5 (1) vRdi,max wird in Abhängigkeit von der Betongüte und der Fugenrauigkeit folgendermaßen berechnet.
Aus der folgenden Tabelle wird die Obergrenze für die Schubtragfähigkeit der Verbundfuge aus den Zulassungen für die Betongüte C25/30 bei rauer Fuge abgelesen und beträgt vRdi,max,Zul = 2,80 N/mm²:[2]
| Zulassungsgrenzen für den Bemessungswert der Schubtragfähigkeit vRdi,max,Zul [N/mm²] | ||
|---|---|---|
| Betongüte | glatte Fuge | raue Fuge |
| C20/25 | 1,13 | 2,40 |
| C25/30 | 1,42 | 2,80 |
| C30/37 | 1,70 | 3,30 |
| C35/45 | 1,98 | 3,60 |
| C40/50 | 2,27 | 3,80 |
| C45/55 | 2,55 | 4,00 |
| C50/60 | 2,83 | 4,10 |
Die maßgebende Schubtragfähigkeit ist der geringste Wert der zuvor bestimmten Werte.
Nachweis
Der Nachweis der Schubtragfähigkeit der Verbundfuge erfolgt folgendermaßen und ist erbracht:
Querkraftbemessung
Für das vorgestellte Beispiel ist rechnerisch keine Querkraftbewehrung erforderlich. Auf eine Ausführung der Berechnung wird daher an dieser Stelle verzichtet.
Verschiedene Beispiele für die Querkraftbemessung bei Elementdecken mit erforderlicher Querkraftbewehrung sind im Betonkalender 2016 [1] zu finden.
Quellen
- ↑ 1,0 1,1 1,2 1,3 1,4 Furche, Johannes u. Bauermeister, Ulrich: Elementbauweise mit Gitterträgern nach Eurocode 2. In Betonkalender 105. Jahrgang (2016), Seiten 469-635
- ↑ 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 Filigran Trägersysteme GmbH & Co. KG: Technische Information Filigran Elementdecke (7/2018)
- ↑ Albert, Andrej u.a.: Schneider Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen. Köln 2018 (23. Auflage)
- ↑ Fingerloos, Frank u. Hegger, Josef u. Zilch, Konrad: Eurocode 2 für Deutschland. Kommentierte Fassung. 2. Auflage, Berlin 2016
Seiteninfo
|