Stahlbetonstütze - Numerisches Verfahren
Im Gegensatz zum Modellstützenverfahren wird hier die Ausmitte nach Theorie II. Ordnung iterativ ermittelt, indem der Krümmungsverlauf über kleinere Stababschnitte ermittelt wird. Die zweifache Integration, näherungsweise numerisch gelöst, der Krümmung κ ergibt die Durchbiegung w, die letztendlich zur Verschiebung der Stabachse führt.
Die Krümmung ermittelt sich mit
An einem differenziellen Balkenelement wird die Verformung eines Balkens durch Momentenbeanspruchung illustriert:
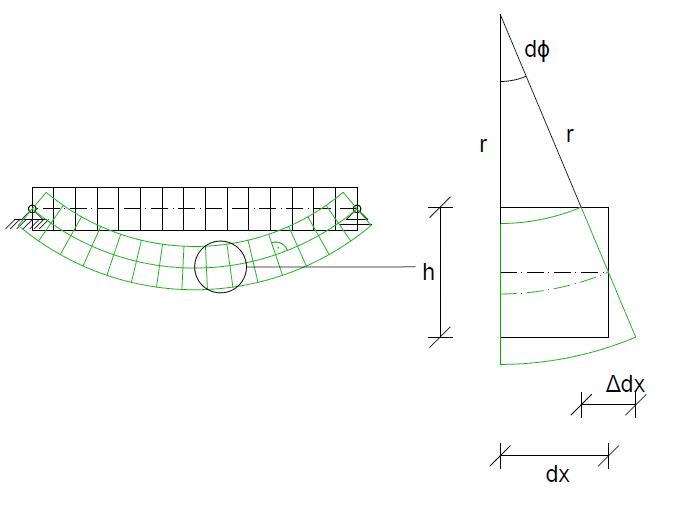
mit
h – der Querschnittshöhe r – dem Radius von Bogenmittelpunkt zur Schwerachse des Querschnitts dx – der infinitesimal kleinsten Länge des differenziellen Balkenelements Δdx – der Längenänderung bezogen auf das Balkenelement - dem differenzielle Winkel zu den Endpunkten der Schwerachse.
Die Dehnungen jeder einzelnen Längsfaser wachsen proportional mit der Entfernung zum Bogenmittelpunkt, anders bekannt als Bernoulli-Hypothese – das Ebenbleiben der Querschnitte. Der Längenzuwachs von im Verhältnis zur Ausgangslänge als dimensionslose Größe ist die Dehnung und nach dem Hooke’schen Gesetz auch folgendermaßen beschrieben
mit
- der Dehnung - der Spannung - dem Elastizitätsmodul.
Das gleiche Verhältnis aus gezeigter Dehnung findet sich wiederum bei
mit
- dem Maß von Schwerachse zu Balkenrand.
Wenn die Spannung gemäß Festigkeitslehre
mit
I – dem Flächenträgheitsmoment
ist, dann gilt auch
Hierbei kürzt sich der Abstand heraus und es verbleibt die Krümmung mit
Es ist zu erkennen, dass das Biegemoment der Krümmung der Biegelinie proportional ist, wobei die Biegesteifigkeit EI den Proportionalitätsfaktor darstellt.
Die Krümmung einfach integriert ergibt den Anstieg der Tangente an der Biegelinie, zweifach integriert ergibt sich die Durchbiegung
oder auch mithilfe des Prinzips der virtuellen Kräfte zu
Bei zu erwartenden Rissen eines Betonbauteils ist die Biegesteifigkeit nicht genau vorherzusagen und mit jedem differenziellem Abschnitt kommt es zu keiner Proportionalität zwischen Moment und Krümmung.
Die Integration des virtuellen Moments überlagert mit dem tatsächlichen Biegemoment führt zur Ermittlung der Durchbiegung an einer Stelle und wird unter Verwendung der Simpson-Formel bei ausreichenden Stützstellen hinreichend genau angenähert:
mit
- der Länge der gleichgroßen Abschnitte -
Es gilt, ein Momenten-Krümmungs-Diagramm mithilfe zweier bekannter Punkte zu erstellen, um auf grafischem Wege den Momenten ihre zugehörige Krümmung zuzuordnen. Dies stellt eine annehmbare Näherung zur eigentlich gekrümmten Momenten-Krümmungs-Linie dar und umgeht so den nichtlinearen Zusammenhang der -Linie. Die Krümmungen selbst können aus dem Dehnungszustand heraus ermittelt werden.
Der erste Punkt ist die Situation vom Übergang in den Zustand II. Hierbei erfolgt eine plötzliche und entlang des Bauteils variierende Verminderung der Querschnittssteifigkeit. Zu erkennen ist dies an einem nun flacheren Anstieg der Linie.
Die Krümmung unter dem Rissmoment im ungerissenen Zustand ergibt sich aus geometrischer Lösung der ermittelten Betonstauchung und Stahlzugdehnung. Es werden Mittelwerte der Baustofffestigkeiten angesetzt, um so eine realistischere Darstellung zu erhalten. Das erste Wertepaar im Momenten-Krümmungsdiagramm ergibt sich aus dem Rissbildungsmoment, je nach Größe der Betonzugfestigkeit und des Widerstandsmoments und der resultierenden Krümmung noch im Zustand I.
Nach Ermittlung der Betondruckspannungen im vollständig gerissenen Zustand unter dem Rissbildungsmoment können die Betonstauchung und die Stahlzugdehnung ermittelt werden.
Anhand des mechanischen Bewehrungsgrades kann die Betonstauchung bei Erreichen der Streckgrenze des Stahls mit Hilfsmitteln wie etwa den Tafeln nach Schmitz ermittelt werden, wohingegen die Stahldehnung unter Berücksichtigung der Zugversteifung des Betons reduziert wird. Die Krümmung ermittelt sich aus demselben geometrischen Zusammenhang wie im Zustand I, das Fließmoment ermittelt sich aus dem inneren Hebelarm und der Stahlzugkraft.
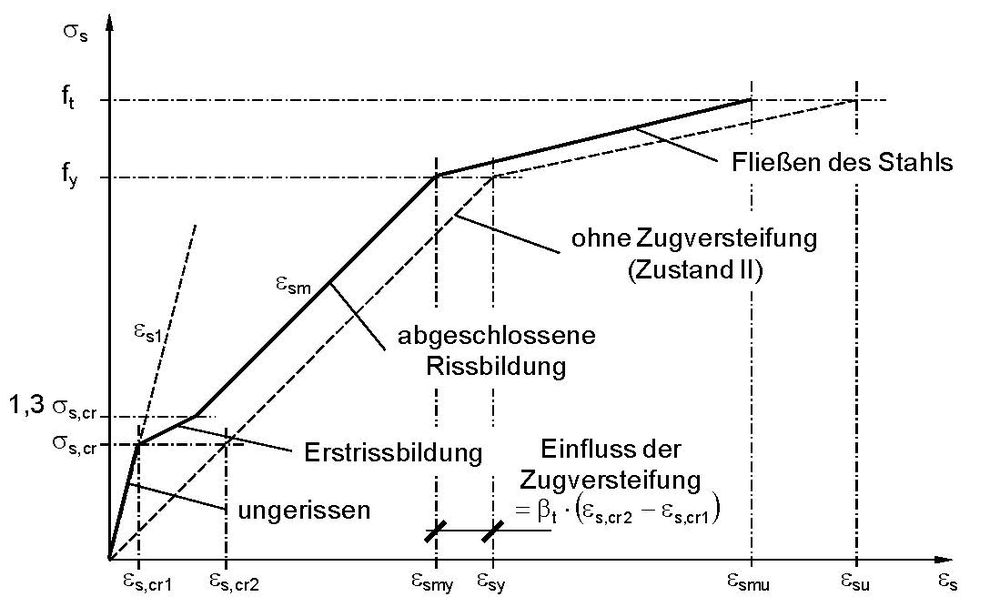
Im Bild[1] zu sehen: Das Spannungs-Dehnungs-Diagramm des Betonstahls. Grafische Verdeutlichung der Zugversteifung des Betons als Differenz einer gedachten Kurve eines von Beginn an gerissenen Querschnitts und eines reellen Spannungs-Dehnungsverlaufs.
Mit dem zweiten Wertepaar kann die rissbedingte Reduzierung des Anstiegs im Momenten-Krümmungs-Diagramm dargestellt werden.
Bei der Verwendung der Simpsonformel sind als Eingangsgrößen das virtuelle Moment an der jeweiligen Stelle x und die grafisch ermittelte Krümmung aus bekanntem Momentenverlauf nötig.
Die ermittelte Verformung an der Stelle der angesetzten Einheitsgröße dient im Falle der Stahlbetonstütze als Ausmitte nach Theorie II. Ordnung und kann, addiert mit den Anteilen aus planmäßiger und ungewollter Ausmitte, zur Ermittlung der Momentenbeanspruchung genutzt werden. Die Bemessung erfolgt nachfolgend mit bekannten Hilfsmitteln und kann bei Übereinstimmung der erforderlichen Bewehrung mit der im Voraus angesetzten Bewehrung beendet werden. Andernfalls ist die Eingangsbewehrung in die Krümmungsermittlung entsprechend anzupassen und eine, nun mit größerer Steifigkeit, weitere Verformungsberechnung erfolgt. Dieser Vorgang ist günstigerweise rechnergesteuert zu vollführen. Eine Vorbemessung mit dem Verfahren mit Nennkrümmung würde im Allgemeinen zu sicher bemessen, eine nachträgliche Reduzierung des Bewehrungsgrades ist dann weiterhin mit einem neuen Iterationsschritt verbunden.
Quellen
- ↑ Bolle, G.: Skript Stahlbetonbau III/Spannbetonbau, Wismar 2012
Seiteninfo
|




















